A ball is thrown straight up from the edge of the roof of a building .A second ball is dropped from the roof 1.00s later. You may ignore air resistance.
a. If the height of the buliding is 20.0m, what must the initial speed be of the first ball if both are to hit the ground at the same time? Consider the same situation, but now let the initial speed v0 of the first ball be given and treat the height (h) of the building as an unknown.
b. What must the height of the building be for both balls to reach the ground at the same time for each of the following values of v0: (i) 6.0ms−1 (ii) 9.5ms−1?
c. If v0 is greater than some values vmax, a value of (h) does same time. Solve for vmax. The value vmin also has a simple physical interpretation. What is it?
For the purpose of doing all four farts with the least reperition of algebra, quantities will be dented symbolically. That is, let
y1=h+v0t−12gt1 and y2=h−12g(t−t0)2.
In this case, t0=1.00s. Setting y1=y2=0, expanding the binomial (t−t0)2, which can be solved for t,
t=12gt20gt0−v0=t021(1−v0gt0) Substiuting this into the expressinon for y1 and setting y1=0 and solving for h as a function of v0 yields after some algebra,
h=12gt20(12gt0−v0)2(gt0−v0)2
a. Using the given value, t0=1.00s and g=9.80ms−2.
h=20.0m=(4.9m)(4.9ms−1−v09.8ms−2−v0)
This has two solutions, one of which is not physical [the first ball is still going up when the second is released, see part C]. The physical solution invlves taking the negative square root before solving for v0, and yields 8.2ms−1
 .
.
b. The above expression gives
for (i) 0.411m and for (ii) 1.15km.
C. As v0 approaches 9.8ms−1, the height h becomes infinite corresponding to a relative velocity at the second ball is throun that approaches zero, If v0≤9.8ms−1, the first ball can never catch the second ball.
d. As v0 approaches 4.9ms−1 the height approaches zero. This corresponds to the first ball being closer and is released. If v0≤4.9ms−1, the first ball will already have roof on the wau down nefore the second ball is released, and the second ball can catch up.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.3
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A ball is thrown straight up from the edge of the roof of a building .A second ball is dropped from the roof 1.00s later. You may ignore air resistance.
a. If the height of the buliding is 20.0m, what must the initial speed be of the first ball if both are to hit the ground at the same time? Consider the same situation, but now let the initial speed v0 of the first ball be given and treat the height (h) of the building as an unknown.
b. What must the height of the building be for both balls to reach the ground at the same time for each of the following values of v0: (i) 6.0ms−1 (ii) 9.5ms−1?
c. If v0 is greater than some values vmax, a value of (h) does same time. Solve for vmax. The value vmin also has a simple physical interpretation. What is it?
View SolutionA ball (A) is thrown straight upfrom the edge the roof of a building. Another ball (B) is dropped from the of 1.00s later. You may ignore air resistance . (a) If the height of the building id 20.0m, what must the initial speed of ball (A) he if bothe are to hit the ground at the same time? (b) On the function of time, measured fro when the first ball is thrown and take origin at ground.
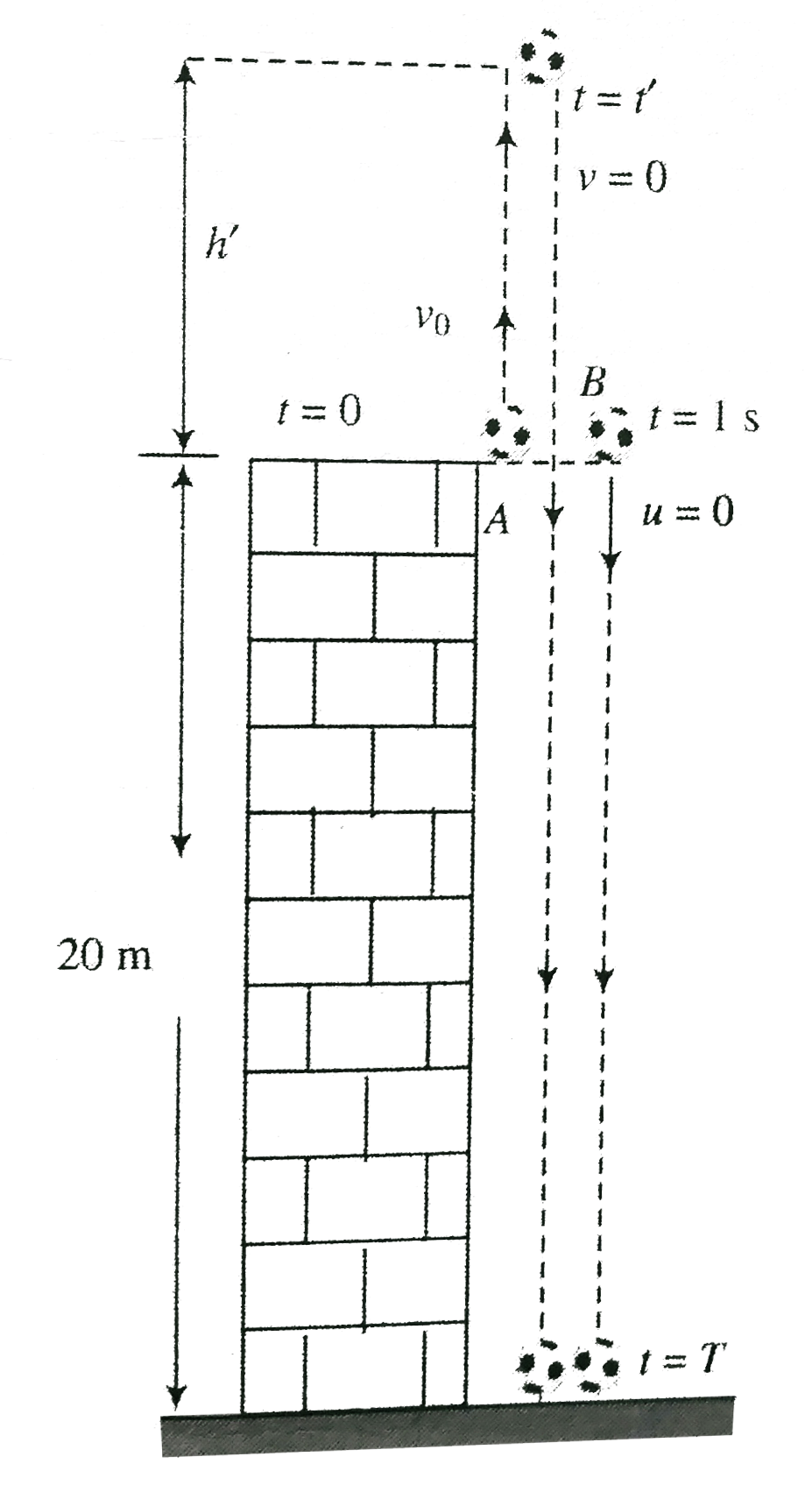 .
.
View Solution
Knowledge Check
A ball is thrown upward from the top of a 25.0 m tall building. The ball's initial speed is 12.0 m/s. At the same instant, a person is running on the ground at a distance of 31.0 m from the building. What must be the average speed of the person if he is to catch the ball at the bottom of the building ?
A8.18 m/sB0.122 m/sC7.20 m/sD0.139 m/sA ball is dropped from the top of an 80 m high tower After 2 s another ball is thrown downwards from the tower. Both the balls reach the ground simultaneously. The initial speed of the second ball is
A10m/sB20m/sC30m/sD40m/sTwo balls of equal size are dropped from the same height from the roof of a building . One ball has twice the mass of the other. When the balls the ground, how do the kinetic energies of the two balls compare ?
AThe lighter one has one fourt has much kinetic energy as the other does.BThe lighter one has one half as much kinetic energy as the other does.CThe lighter one has the same kinetic energy as the other does.DThe lighter one has twice as much kinetic energy as the other does.
A ball is thrown horizontally and at the same time another ball is dropped down from the top of a tower Will both the balls reach the ground at the same time ?
View SolutionThe ball is dropped from a bridge 122.5m above a rivet, After the ball has been falling for 2 s, a second ball is thrown straight down after it. What must its initial velocity be so that bothe hit the warer at the same time ?
View SolutionThe ball is dropped from a bridge 122.5m above a river, After the ball has been falling for 2 s, a second ball is thrown straight down after it. What must its initial velocity be so that both hit the water at the same time ?
View SolutionA ball is dropped from a top of a 100 m high building. At the ssame time another ball is thrown up from the ground with a speed of 20ms−1. At what time will the balls meet?
View SolutionConsider the situation as shown.
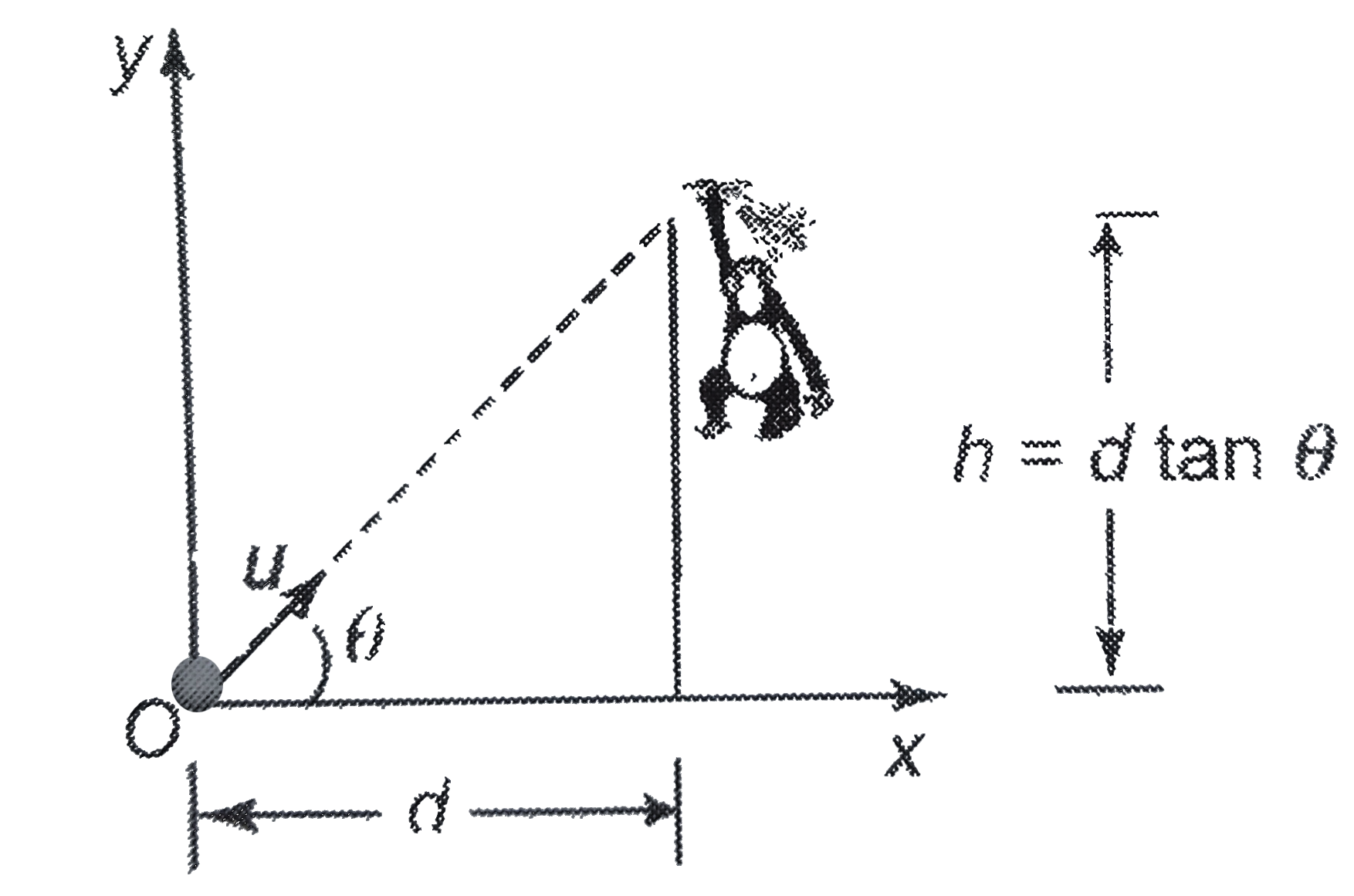
When a ball is thrown aiming the monkey, at the same time the monkey drops himself. Will the ball hit the monkey ?
View Solution
