A ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
To find the average force exerted by a ball of mass m on the floor during a long time interval when it is dropped from a height h and rebounds elastically, we can follow these steps:
1. Determine the Velocity Just Before Impact:
When the ball is dropped from a height h, we can use the third equation of motion to find the velocity just before it hits the ground. The equation is:
v=√2gh
where g is the acceleration due to gravity.
2. Calculate the Change in Velocity:
The ball rebounds elastically, meaning it will have the same speed but in the opposite direction after bouncing. Thus, the change in velocity (Δv) can be calculated as:
Δv=vfinal−vinitial=√2gh−(−√2gh)=2√2gh
3. Determine the Time of Collision:
Let’s denote the time taken to fall to the ground as t0 and the time taken to rise back to the same height as t0 as well. Therefore, the total time for the ball to fall and then rise back is:
Δt=2t0
The time t0 can be calculated using:
t0=√2hg
Hence, the total time becomes:
Δt=2√2hg
4. Calculate the Average Force:
The average force (Favg) exerted by the ball on the floor can be calculated using the formula:
Favg=ΔpΔt
where Δp is the change in momentum. The change in momentum can be expressed as:
Δp=mΔv=m(2√2gh)
Therefore, substituting into the average force formula gives:
Favg=m(2√2gh)2√2hg
5. Simplify the Expression:
Simplifying the expression:
Favg=m(2√2gh)2√2hg=mg
Thus, the average force exerted by the ball on the floor during a long time interval is:
Favg=mg
Final Answer:
The average force exerted by the ball on the floor is mg.
When the ball is dropped from a height h, we can use the third equation of motion to find the velocity just before it hits the ground. The equation is:
v=√2gh
where g is the acceleration due to gravity.
The ball rebounds elastically, meaning it will have the same speed but in the opposite direction after bouncing. Thus, the change in velocity (Δv) can be calculated as:
Δv=vfinal−vinitial=√2gh−(−√2gh)=2√2gh
Let’s denote the time taken to fall to the ground as t0 and the time taken to rise back to the same height as t0 as well. Therefore, the total time for the ball to fall and then rise back is:
Δt=2t0
t0=√2hg
Hence, the total time becomes:
Δt=2√2hg
The average force (Favg) exerted by the ball on the floor can be calculated using the formula:
Favg=ΔpΔt
where Δp is the change in momentum. The change in momentum can be expressed as:
Δp=mΔv=m(2√2gh)
Therefore, substituting into the average force formula gives:
Favg=m(2√2gh)2√2hg
Simplifying the expression:
Favg=m(2√2gh)2√2hg=mg
Thus, the average force exerted by the ball on the floor during a long time interval is:
Favg=mg
The average force exerted by the ball on the floor is mg.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A ball is dropped from height 'h' as shown.The collision is perfectly inelastic. Select the correct alternative (s)
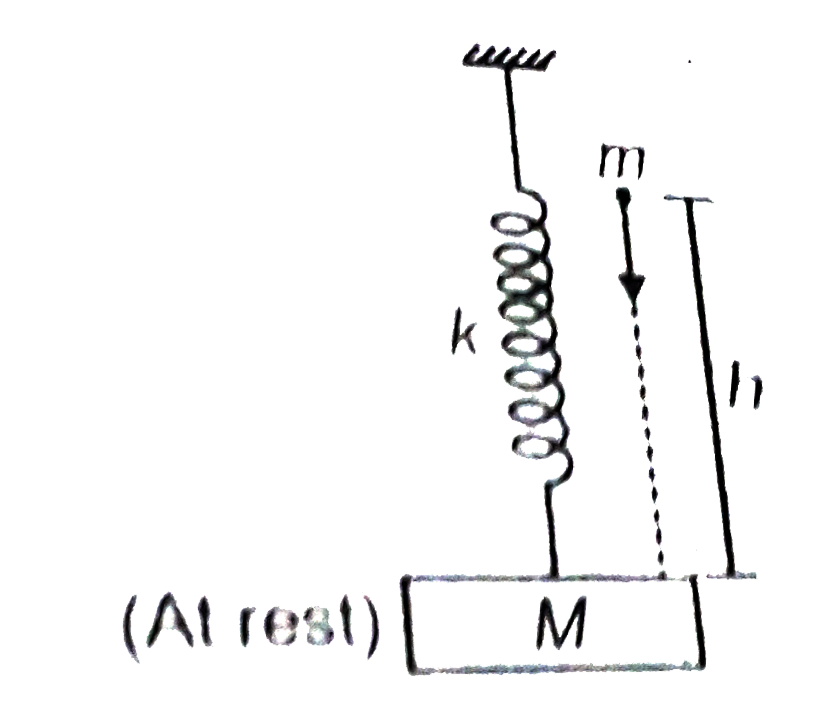
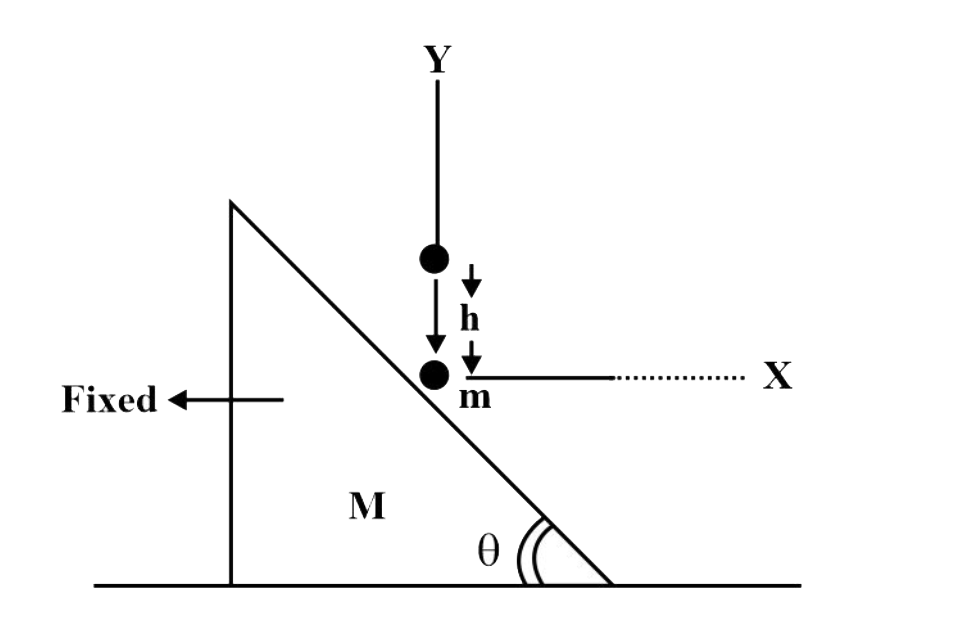
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is √2gh , then θ is
View Solution
Knowledge Check
A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBeh2Ce4hDhe4
A ball is dropped onto a floor from a height of 10m. If 20% of its initial energy is lost,then the height of bounce is
View SolutionA ball is dropped on the ground from a height of 1m. The coefficient of restitution is 0.6. The height to which the ball will rebound is
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
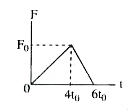
Average force exerted by the bat on the ball is
View SolutionA rubber ball of mass 0.4 kg hits the ground at same angle without any change in speed . If the speed of ball is 1 m/s and the period of contact between the ball and floor is 0.4 s, find the average force exerted by the ball on the ground .
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
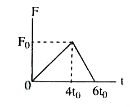
Maximum force exerted by the bat on the ball is
View SolutionA ball is dropped on a floor from a height h. If the coefficient of restitution is e, find the height to which the ball will rise after touching the floor and the time it will take to come to rest again.
View SolutionA ball of mass m strikes the fixed inclined plane after falling through a height h. if it rebounds elastically. The impulse on the ball is :
View Solution
