A ball of mass m is moving normally towards a walll of mass M(>>m) with the velocity 4m/s. The wall is also moving. After striking elastically with the wall , velocity of ball becomes 8m/s. Find the speed of the wall:
4m/s
2m/s
2√2m/s
4√2m/s
The correct Answer is:D
Let V be the velocity of ball. Relative velocity of separation = relative velocity of approach. 8−V=4+V, if wall is moving towards left V=2m/s towards left and 87×V=4−V, if wall is moving towards right V=−2m/s=2m/s toward left.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Assertion Reasoning
Explore 17 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Circular Motion In Vertical Plane
Explore 21 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ?
View Solution
Knowledge Check
A ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
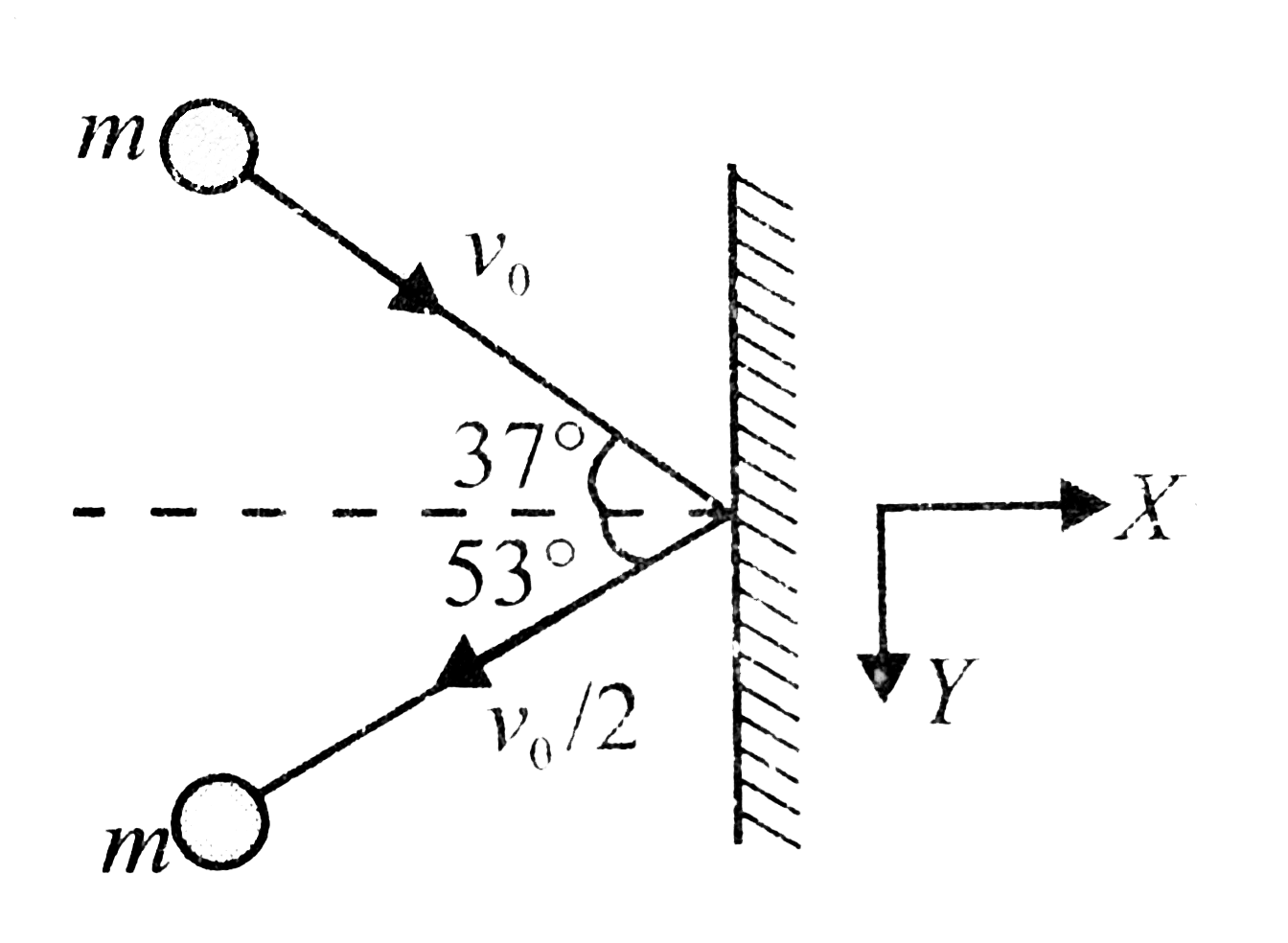 Amv02ˆjB−mv02ˆjC−mv05ˆjDnone of these
Amv02ˆjB−mv02ˆjC−mv05ˆjDnone of theseA wall moving with velocity 2cms−1 towards the ball and ball is moving towards the wall with a velocity 10cms−1. It hits the wall normally and makes elastic collision with wall. The velocity of ball after collision with wall in cms−1.
A12B8C14D16A ball of mass 'm' moves normal to a wall with a velocity 'u' and rebounds with the same speed. The change in momentum of the ball during the rebounding is
A2mu towards the wallB2mu away from the wallCzeroDmu away from the wall
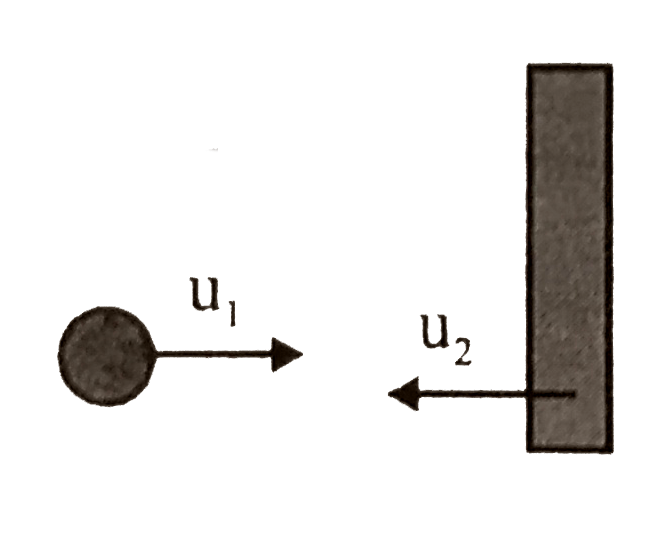
A particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
View SolutionA ball of mass 5 kg moving velocity 3m/s impinges direction on another ball of mass 2 kg moving with velocity 0.5m/s towards the first ball. Find the velocity after impact, if e=47
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA molecule of mass m moving at a velocity v impinges elastically on the wall at an angle a with the wall. Then
View Solution