A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
(θ+β)<90∘ if the wall is smooth
if the wall is rough , coefficient of restitution =tanβ/cosθ
if the wall is rough, coefficient of restition
<tanβ/cotθ
none of these
The correct Answer is:A, C, D
To solve the problem of a ball striking a wall and rebounding, we can break it down into several steps:
Step 1: Understand the situation
A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall. After striking the wall, it rebounds at an angle β with the surface. The angles θ and β are defined with respect to the normal and the surface, respectively.
Step 2: Resolve the velocity into components
The initial velocity →u can be resolved into two components:
- Perpendicular to the wall (normal component): ucosθ
- Parallel to the wall (tangential component): usinθ
Step 3: Apply the coefficient of restitution
The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach. For a smooth wall, there is no friction, and the tangential component remains unchanged. Thus, we have:
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}} = \frac{V_{\perpendicular}}{u \cos \theta}
Where V_{\perpendicular} is the component of the rebound velocity in the direction normal to the wall.
Step 4: Calculate the rebound velocity
From the above equation, we can express V_{\perpendicular} :
V_{\perpendicular} = e \cdot u \cos \theta
Step 5: Analyze the tangential component
Since the wall is smooth, the tangential component of the velocity does not change:
usinθ=Vsinβ
Where V is the magnitude of the rebound velocity.
Step 6: Relate angles using geometry
From the geometry of the problem, we know that:
α+β=90∘
Where α is the angle made by the rebound velocity with the normal.
Step 7: Substitute and simplify
Using the relationship between angles:
sinβ=cosαandcosβ=sinα
We can substitute these into our equations to find relationships between θ, β, and e.
Step 8: Analyze the conditions for a rough wall
If the wall is rough, the coefficient of restitution changes, and we can express it in terms of the angles:
e=tanβcosθ
Step 9: Conclusion
From the analysis, we conclude that:
- If the wall is smooth, θ+β<90∘ holds true.
- If the wall is rough, the coefficient of restitution is given by e=tanβcosθ.
A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall. After striking the wall, it rebounds at an angle β with the surface. The angles θ and β are defined with respect to the normal and the surface, respectively.
The initial velocity →u can be resolved into two components:
- Perpendicular to the wall (normal component): ucosθ
- Parallel to the wall (tangential component): usinθ
The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach. For a smooth wall, there is no friction, and the tangential component remains unchanged. Thus, we have:
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}} = \frac{V_{\perpendicular}}{u \cos \theta}
Where V_{\perpendicular} is the component of the rebound velocity in the direction normal to the wall.
From the above equation, we can express V_{\perpendicular} :
V_{\perpendicular} = e \cdot u \cos \theta
Since the wall is smooth, the tangential component of the velocity does not change:
usinθ=Vsinβ
Where V is the magnitude of the rebound velocity.
From the geometry of the problem, we know that:
α+β=90∘
Where α is the angle made by the rebound velocity with the normal.
Using the relationship between angles:
sinβ=cosαandcosβ=sinα
We can substitute these into our equations to find relationships between θ, β, and e.
If the wall is rough, the coefficient of restitution changes, and we can express it in terms of the angles:
e=tanβcosθ
From the analysis, we conclude that:
- If the wall is smooth, θ+β<90∘ holds true.
- If the wall is rough, the coefficient of restitution is given by e=tanβcosθ.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
 View Solution
View SolutionA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
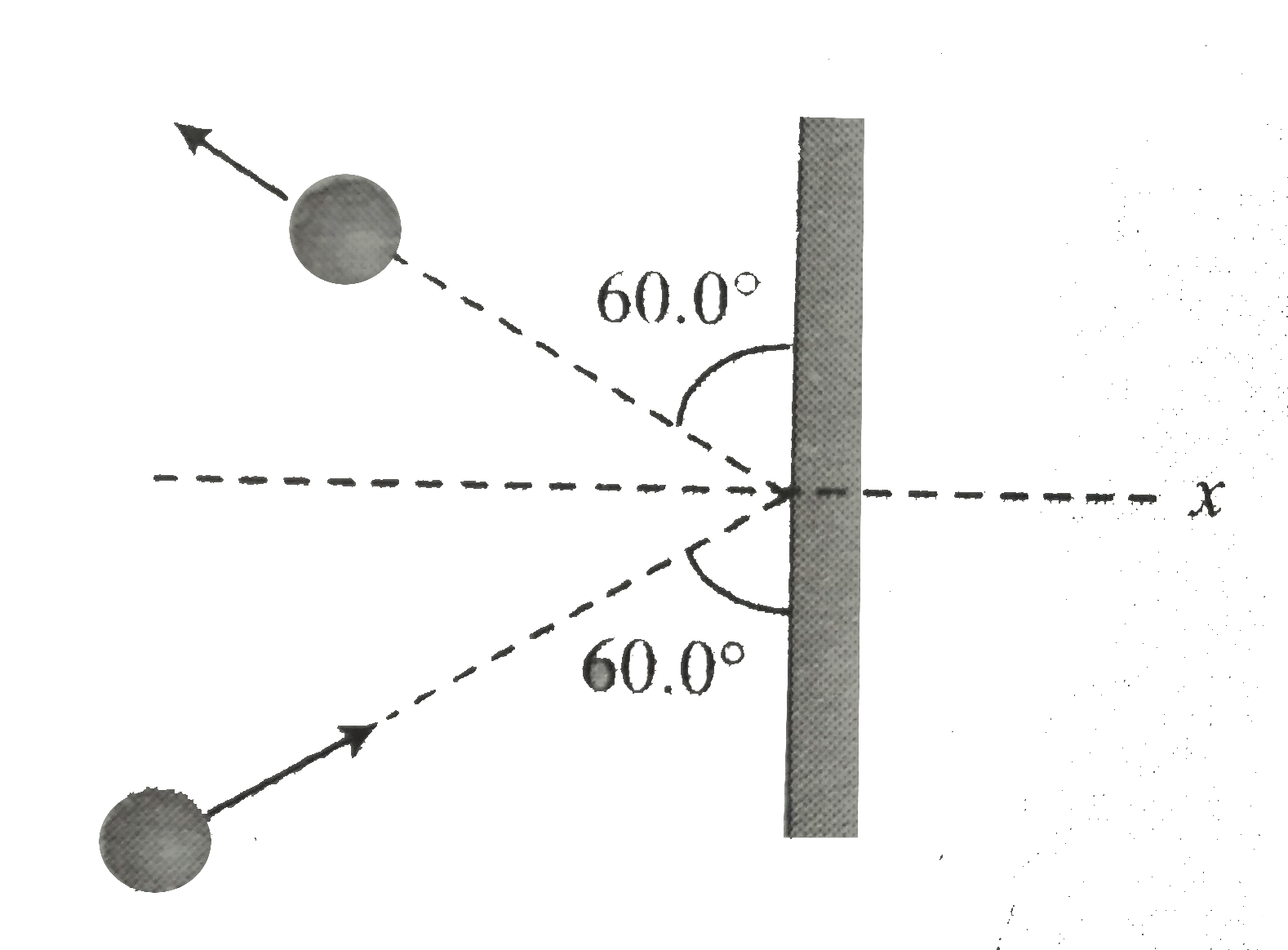
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
 View Solution
View SolutionA ball strikes the ground at an angle α. and rebound at an angle β. with the verticlal as shown in the figure .Then ,
 View Solution
View SolutionA 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View Solution2000 small balls, each weighing 1 g, strike one square cm of area per second with a velocity of 100 m/s normal to the surface and rebounds with the same velocity. The pressure on the surface is
View SolutionA ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collison with a vertical wall and returns to ground. The total time of flight of the ball is
View Solution

