A ball with initial momentum P collides with rigid wall elastically. If P1 be it's momentum after collision then
P1=P
P1=−P
P1=2P
P1=−2P
The correct Answer is:B
To solve the problem of a ball colliding elastically with a rigid wall, we can follow these steps:
Step 1: Understand the Initial Conditions
The ball has an initial momentum P. We can express this in terms of mass m and initial velocity u1:
P=m⋅u1
Step 2: Identify the Type of Collision
The collision is elastic, which means both momentum and kinetic energy are conserved. The coefficient of restitution e for an elastic collision is equal to 1.
Step 3: Apply the Coefficient of Restitution
The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
In this case, the wall is rigid and stationary, so its velocity u2=0. The velocities involved are:
- Velocity of approach: u1−u2=u1−0=u1
- Velocity of separation: v2−v1 (where v1 is the velocity of the ball after the collision and v2=0 for the wall)
Thus, we have:
e=0−v1u1−0=−v1u1
Since e=1:
1=−v1u1
Step 4: Solve for the Final Velocity
From the equation above, we can rearrange to find v1:
−v1=u1⟹v1=−u1
Step 5: Calculate the Momentum After Collision
Now, we can calculate the momentum after the collision P1:
P1=m⋅v1
Substituting v1:
P1=m⋅(−u1)=−m⋅u1
Since P=m⋅u1, we can substitute:
P1=−P
Final Answer
The momentum of the ball after the collision is:
P1=−P
---
The ball has an initial momentum P. We can express this in terms of mass m and initial velocity u1:
P=m⋅u1
The collision is elastic, which means both momentum and kinetic energy are conserved. The coefficient of restitution e for an elastic collision is equal to 1.
The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
In this case, the wall is rigid and stationary, so its velocity u2=0. The velocities involved are:
- Velocity of approach: u1−u2=u1−0=u1
- Velocity of separation: v2−v1 (where v1 is the velocity of the ball after the collision and v2=0 for the wall)
e=0−v1u1−0=−v1u1
Since e=1:
1=−v1u1
From the equation above, we can rearrange to find v1:
−v1=u1⟹v1=−u1
Now, we can calculate the momentum after the collision P1:
P1=m⋅v1
Substituting v1:
P1=m⋅(−u1)=−m⋅u1
Since P=m⋅u1, we can substitute:
P1=−P
The momentum of the ball after the collision is:
P1=−P
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application
6 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A ball A moving with momentum 2ˆi+4ˆj collides with identical ball B moving with momentum 6ˆj . After collision momentum of ball B is 10ˆj . Which of the following statement is correct?
View SolutionA body X with a momentum p collides with another identical stationary body Y one dimensionally. During the collision, Y gives an impulse J to body X. Then coefficient of restitution is
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
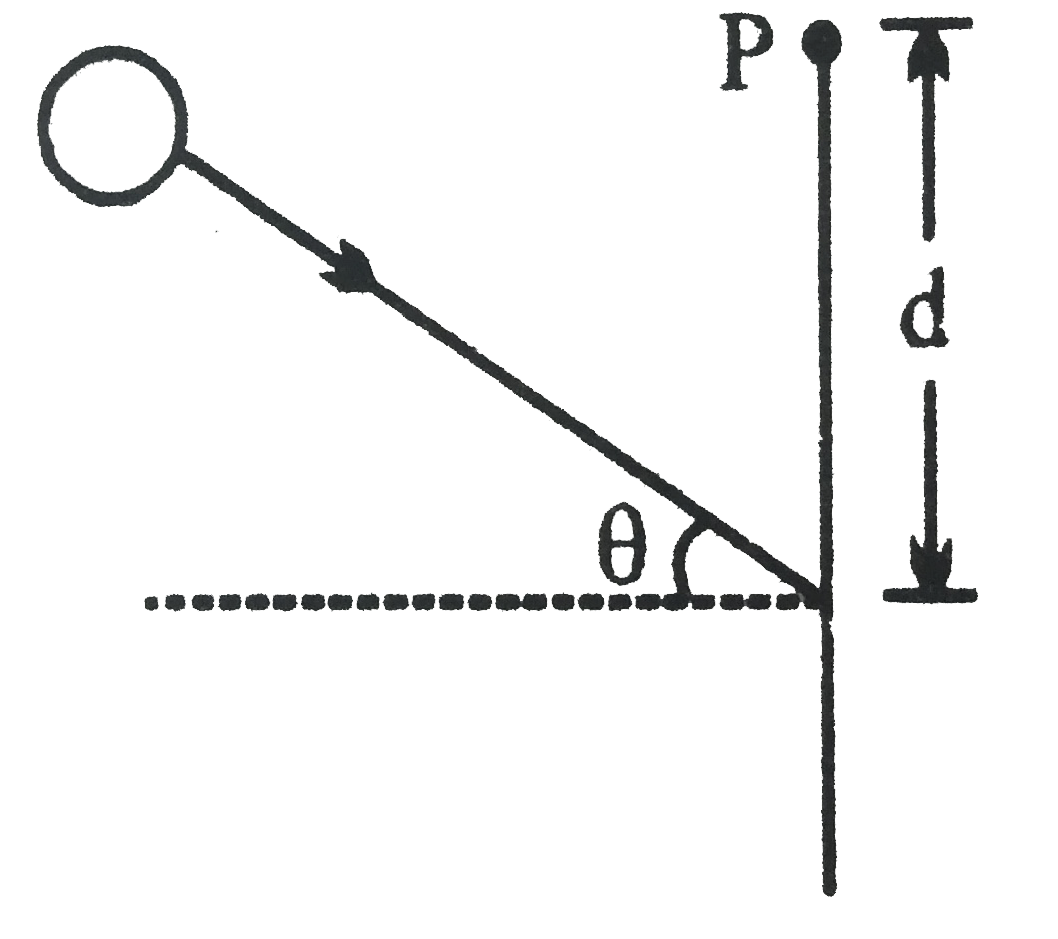 .
.
View SolutionTwo particles of equal masses moving with same momentum collide perfectly inelastically. After the collision the combined mass moves with half of the speed of the individual masses. The angle between the initial momenta of individual particle is
View SolutionA particle of mass m, kinetic energy K and momentum p collides head on elastically with another particle of mass 2m at rest. After collision, :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9(t)None
View SolutionA particle A of mass m and initial velocity v collides with a particle of mass m/2 which is at rest. The collision is head on, and elastic. The ratio of the de-broglie wavelength λAandλB after the collision is
View SolutionA heavy ball moving with speed v collides with a tiny ball. The collision is elastic, then immediately after the impact, the second ball will move with a speed approximately equal to
View SolutionA ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle calculate the change in momentum
View SolutionA ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ?
View SolutionA body of mass 'm' moving with certain velocity collides with another identical body at rest. If the collision is perfectly elastic and after the collision both the bodies moves
View Solution
