A ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ?
5 m/s away from the wall
9 m/s away from the wall
3 m/s away from the wall
6 m/s away from the wall
To solve the problem, we will use the principles of conservation of momentum and the coefficient of restitution for elastic collisions.
1. Identify the given values:
- Mass of the ball = m
- Mass of the wall = M
- Initial speed of the ball, u1=4m/s (towards the wall)
- Initial speed of the wall, u2=−1m/s (towards the ball, hence negative)
2. Write the conservation of momentum equation:
The total momentum before the collision equals the total momentum after the collision.
mu1+Mu2=mv1+Mv2
Substituting the values:
m(4)+M(−1)=mv1+Mv2
This simplifies to:
4m−M=mv1+Mv2(Equation 1)
3. Use the coefficient of restitution:
For an elastic collision, the coefficient of restitution e=1. The equation for the coefficient of restitution is:
e=v2−v1u1−u2
Substituting the known values:
1=v2−v14−(−1)=v2−v15
Rearranging gives:
v2−v1=5(Equation 2)
4. Substituting Equation 2 into Equation 1:
From Equation 2, we can express v2 in terms of v1:
v2=v1+5
Substitute this into Equation 1:
4m−M=mv1+M(v1+5)
Expanding gives:
4m−M=mv1+Mv1+5M
Combining terms:
4m−M=(m+M)v1+5M
Rearranging gives:
(m+M)v1=4m−6M
Therefore:
v1=4m−6Mm+M
5. Analyzing the result:
Since M (mass of the wall) is much larger than m (mass of the ball), we can approximate:
v1≈−6MM=−6m/s
This indicates that the ball will be moving away from the wall at a speed of approximately 6m/s after the collision.
Conclusion:
The speed of the ball after the collision will be slightly less than 6m/s because the wall's mass is significantly larger, which affects the final speed of the ball.
- Mass of the ball = m
- Mass of the wall = M
- Initial speed of the ball, u1=4m/s (towards the wall)
- Initial speed of the wall, u2=−1m/s (towards the ball, hence negative)
The total momentum before the collision equals the total momentum after the collision.
mu1+Mu2=mv1+Mv2
Substituting the values:
m(4)+M(−1)=mv1+Mv2
This simplifies to:
4m−M=mv1+Mv2(Equation 1)
For an elastic collision, the coefficient of restitution e=1. The equation for the coefficient of restitution is:
e=v2−v1u1−u2
Substituting the known values:
1=v2−v14−(−1)=v2−v15
Rearranging gives:
v2−v1=5(Equation 2)
From Equation 2, we can express v2 in terms of v1:
v2=v1+5
Substitute this into Equation 1:
4m−M=mv1+M(v1+5)
Expanding gives:
4m−M=mv1+Mv1+5M
Combining terms:
4m−M=(m+M)v1+5M
Rearranging gives:
(m+M)v1=4m−6M
Therefore:
v1=4m−6Mm+M
Since M (mass of the wall) is much larger than m (mass of the ball), we can approximate:
v1≈−6MM=−6m/s
This indicates that the ball will be moving away from the wall at a speed of approximately 6m/s after the collision.
The speed of the ball after the collision will be slightly less than 6m/s because the wall's mass is significantly larger, which affects the final speed of the ball.
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A ball of mass m approaches a wall of mass M (M>>m), with speed 2 ms−1 along the normal to the wall. The speed of wall is 1 ms−1 towards the ball. The speed of the ball after an elastic collision with the wall is-
View SolutionA particle of mass m is projected towards a wall such that the angle of incidence is θ and the speed just before collision is u. Assuming that the wall is smooth and the collision is elastic, show that the ball rebounds at same angle.
View Solution
Knowledge Check
A ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2muA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘tA ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzero
A ball of mass 1kg strikes a heavy plarform elastically, moving upwards with a velocity of 5m/s . The speed of the ball just before the collision is 10m/s downwards. Then the impulse imparted by the platform on the ball is

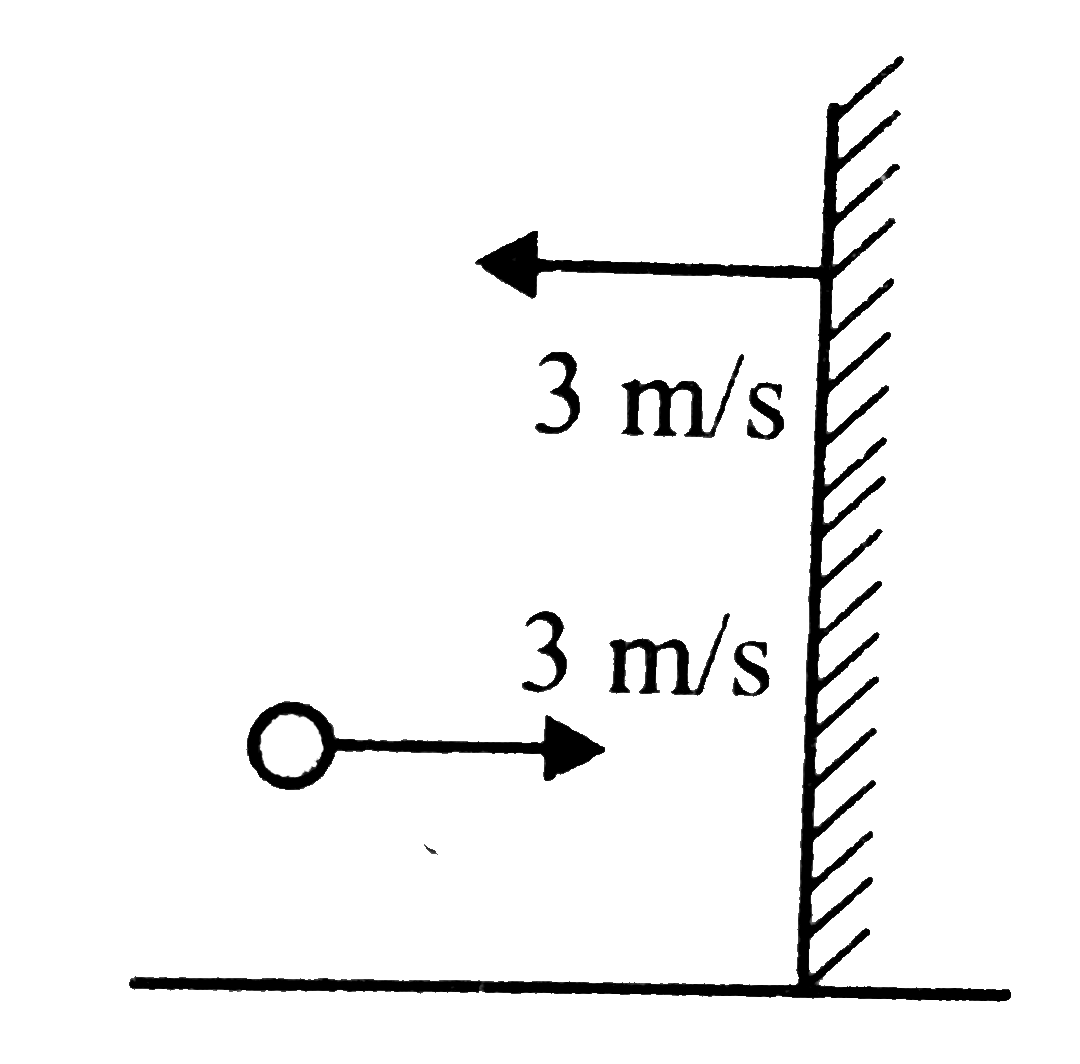
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
View SolutionA ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View SolutionA small ball of mass m moving with speed v collides elastically with a simple pendulum with bob of mass m at rest. The maximum height attained by the bob after collision is
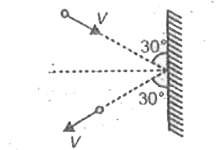
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View Solution
