A balloon starts rising from the earth's surface. The ascension rate is constant and equal to . Due to the wind. The balloon gathers the horizontal velocity component , where k is a constnat and y is the height of ascent. Find how the following quantities depednd on the height of ascent.
(a) the horizontal drift of the balloon x (y)
(b) the total tangential and normal accelrations of the balloon.
(a) .............(i)
............(ii)
Dividing Eqn. (i) by Eqn. (ii) we get
Integrating we get
This is the desired trajector of the particle, which is and equation of a parabola.
(b) For finding the tangential and normal accelrations, we require and expression for the speed as a function of height y
and
Therefore, tangential accelration,
Now, the total accelration is,
Normal accleration,
Topper's Solved these Questions
Similar Questions
A balloon starts rising from the surface of the Earth. The ascertion rate is constant and equal to v0. Due to the wind the balloon
View SolutionA balloon starts rising from the surface of the earth with vertical component of velocity v0. The balloon gathers a horizontal velocity vx=ay, where a is a constant and y is the height from the surface of the earth, due to a horizontal wind. Determine
(a) the equation of trajectory of the balloon.
(b) the tangential, normal and total acceleration of the balloon as function of y.
View Solution
Knowledge Check
A balloon starts rising from the ground with an acceleration of 1.25ms−2. After 8 seconds, a stone is released from the balloon. After releasing, the stone will:
Acover a distance of 50 m till it strikes the ground.Bhave a displacement of 50 till it reaches the ground.Creach the ground in 4 seconds.Dbegin to move down instantaneously.Two ballons are simultaneously released from two buildings A and B. Balloon from A rises with constant velocity 10ms−1 While the other one rises with constant velocity of 20ms−1 Due to wind the balloons gather horizontal velocity Vx=0.5 y, where 'y' is the height from the point of release. The buildings are at a distance of 250 m & after some time 't' the balloons collide.
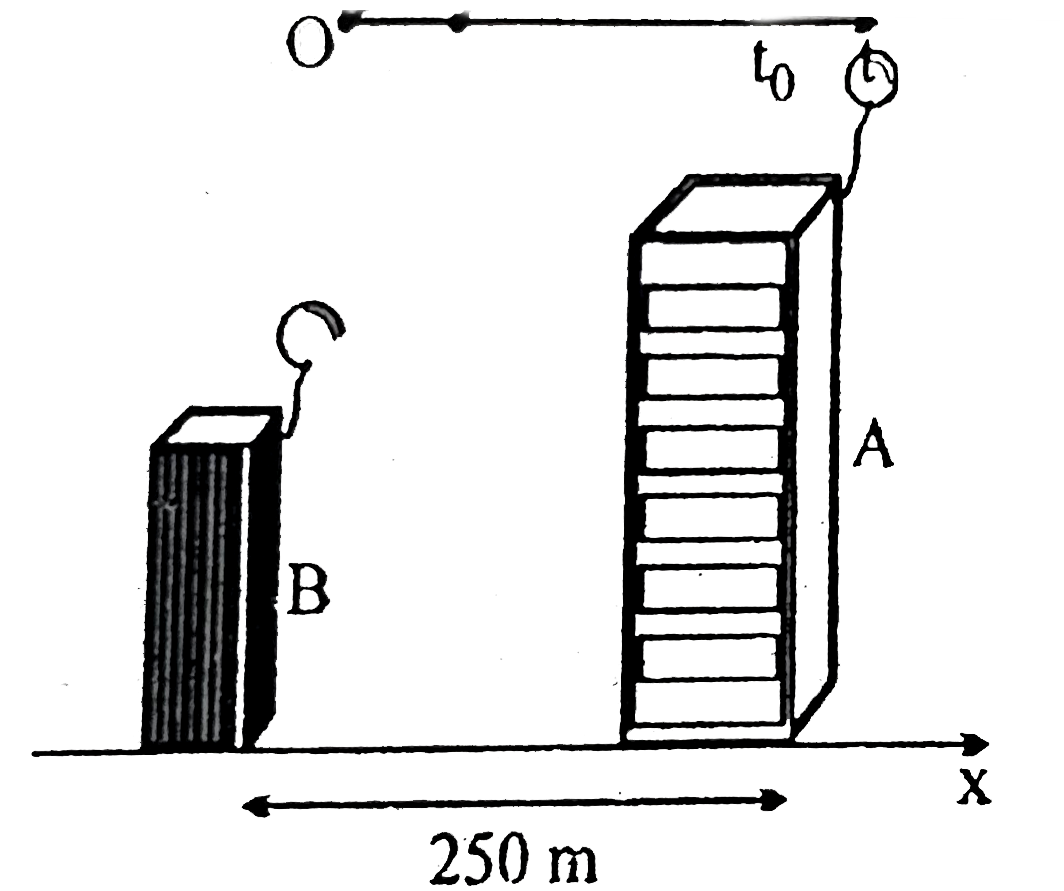 At=5secBdifference in height of buildings in 100mCdifference in height of buildings is 500Dt=0 sec
At=5secBdifference in height of buildings in 100mCdifference in height of buildings is 500Dt=0 secA ball is thrown vertically upward with a velocity u from balloon descending with a constant velocity v. The ball will pass by the balloon after time
Au+v2gB2u+vgC2u+2vgD(u+v)g
A balloon starts rising from the surface of the earth with a verticle component of velocity v0. The baloon gathes a horizontal velocity vx=λy, where λ is a constant and y is the height from the surface of earth, due to a horizontaln wind. determine (a) the equation of trajectory and (b) the tangential, normal and total acceleration of the balloon as a function of y.
View SolutionA particle is released from a certain height H=400m. Due to the wind, the particle gathers the horizontal velocity component vx=aywhere a =(√5)s−1 and y is the vertical displacement of the particle from the point of release, then find
(a) the horizontal drift of the particle when it strikes the ground ,
(b) the speed with which particle strikes the ground.
View SolutionIf the height of the orbit of a satellite from the earth surface is increased , the tangential velocity of satellite will …………….
View SolutionAt a certain place, the horizontal component B0 and the vertical component V0 of the earth's magnetic field are equal in magnidude. The total intensity at the place will be
View SolutionA balloon starts rising from ground with an acceleration of 1.25m/sec2. A 8 seconds a stone is released from the balloon. The maximum height from the ground reached by stone will be.
View Solution
