A bar of mass m=0.50kg lying on a horizontal plane with a friction coefficient k=0.10 is attached to the wall by means of a horizontal non− deformed spring. The stiffness of the spring is equal to x=2.45N/cm, its mass is negligibl . The bar was displaced so that the spring was stretched by x0=3.0cm, and then released. Find :
(a) the period of oscillation of the bar ,
(b) the total number os osciallations that the bar performs untial it stops completely.
We shall denote the stiffness constant by k. Suppose the spring is stretched by x0. The bar in then subject to two horizontal forces (1) restoring force −kx and (2) friction kmg opposing motion. If
x0>kgmk=Δ
the bar will come back.
( If x0≤Δ, the bar will stay put . )
The equation of the bar when it is moving to the left is
m..x=−kx+kmg
This equation has the solution
x=Δ+(x0−Δ)cos√kmt
where we have used x=x0,.x=0 at t=0 . This solution is onely valid till the bar comes to rest. This happens at
t1=π/√km
and at that time x=x1=2Δ−x0. ifx0>2Δ the tendency of the rod will now be to move to the right. ( if Δ<x0<2Δ the rod will stay put now ) Now the equation for rightward motion becomes
m..x=−kx−kmg
( the friction force has reversed ).
We notice that the rod will move to the right only if
k(x0−2Δ)>kmg i.e.x0>3Δ
In this case the solution is
x=−Δ+(x0−3Δ)cos√kmt
Since x=2Δ−x0and .x=0 at t=t1=π/√km.
The rod will next come to rest at
t=t2=2π/√km
and at that instant x=x2=x0−4Δ. However the rod will stay put unless x0>5Δ
Thus
(a) time period of one full oscillation =2π/√km.
(b) There is no oscillation if 0<x0<Δ
One half oscillation if Δ<x0<3Δ
2 half oscillation if 3Δ<x0<5Δ etc
We can say that the number of full oscillation is one half of the integern where n=[x0−Δ2Δ]
where[x]= smalles non- negative integer greater than x.

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
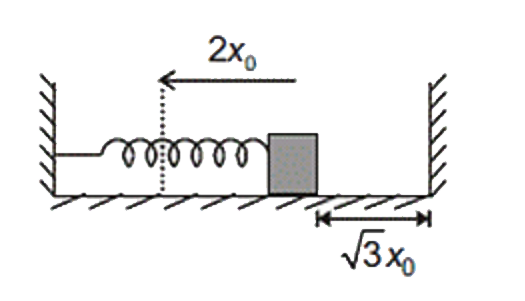
One end of a spring of force constant K is fixed to a vertical wall and other to a body of mass m resting on smooth horizontal surface. There is another wall at a distance of √3x0 from the body. If all the collisions are elastic and spring is compressed by 2x0and released, then the time period of oscillation is
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View Solution
Knowledge Check
A mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
A3.1cmB6.2cmC9.3cmD12.4cmOne end of a spring of force constant K is fixed to a vertical wall and other to a body of mass m resting on smooth horizontal surface. There is another wall at a distance of √3x0 from the body. If all the collisions are elastic and spring is compressed by 2x0and released, then the time period of oscillation is
 A5π3√mKB5π4√mKC3π2√mKD4π3√mK
A5π3√mKB5π4√mKC3π2√mKD4π3√mKWhen a mass of 1 kg is suspended from a spring, it is stretched by 0.4m. A mass of 0.25 kg is suspended from the spring and the spring is allowed to oscillate. If g=10m/s2, then its period of oscillation will be
A0.5 secB0.4 secC0.628 secD1.5 sec
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View Solution
