A barometer kept in an elevator accelerating upwards reads 76 cm of Hg. If the elevator is accelerating upwards at 4.9ms−2 , what will be the air pressure in the elevator?
The correct Answer is:(114cmof Hg)
To find the air pressure in the elevator when it is accelerating upwards, we can follow these steps:
Step 1: Understand the situation
The barometer reads 76 cm of Hg when the elevator is at rest or moving at constant velocity. When the elevator accelerates upwards, the effective acceleration due to gravity increases.
Step 2: Determine the effective acceleration
The effective acceleration g′ when the elevator is accelerating upwards can be calculated as:
g′=g+a
where:
- g is the acceleration due to gravity (approximately 9.8m/s2),
- a is the upward acceleration of the elevator (4.9m/s2).
Substituting the values:
g′=9.8m/s2+4.9m/s2=14.7m/s2
Step 3: Relate the height of the mercury column to pressure
The pressure exerted by a column of mercury is given by:
P=ρgh
where:
- P is the pressure,
- ρ is the density of mercury (approximately 13,600kg/m3),
- g is the effective acceleration due to gravity,
- h is the height of the mercury column.
Step 4: Calculate the new height of the mercury column
Since the barometer reads 76 cm of Hg at normal conditions, we can find the new height h′ of the mercury column under the new effective gravitational acceleration:
P0=ρgh⟹h′=P0ρg′
Given that the original pressure P0 corresponds to 76 cm of Hg, we can express this in meters:
h′=0.76m⋅9.8m/s214.7m/s2
Step 5: Calculate the new height
Calculating h′:
h′=0.76⋅9.814.7≈0.51m (or 51 cm)
Step 6: Calculate the air pressure in the elevator
The air pressure in the elevator can be calculated using the formula:
P=ρg′h′
Substituting the values:
P=13,600kg/m3⋅14.7m/s2⋅0.51m
Calculating this gives:
P≈101,325Pa (or 1 atm)
Final Result
The air pressure in the elevator when it is accelerating upwards at 4.9m/s2 is approximately 101,325Pa.
The barometer reads 76 cm of Hg when the elevator is at rest or moving at constant velocity. When the elevator accelerates upwards, the effective acceleration due to gravity increases.
The effective acceleration g′ when the elevator is accelerating upwards can be calculated as:
g′=g+a
where:
- g is the acceleration due to gravity (approximately 9.8m/s2),
- a is the upward acceleration of the elevator (4.9m/s2).
g′=9.8m/s2+4.9m/s2=14.7m/s2
The pressure exerted by a column of mercury is given by:
P=ρgh
where:
- P is the pressure,
- ρ is the density of mercury (approximately 13,600kg/m3),
- g is the effective acceleration due to gravity,
- h is the height of the mercury column.
Since the barometer reads 76 cm of Hg at normal conditions, we can find the new height h′ of the mercury column under the new effective gravitational acceleration:
P0=ρgh⟹h′=P0ρg′
Given that the original pressure P0 corresponds to 76 cm of Hg, we can express this in meters:
h′=0.76m⋅9.8m/s214.7m/s2
Calculating h′:
h′=0.76⋅9.814.7≈0.51m (or 51 cm)
The air pressure in the elevator can be calculated using the formula:
P=ρg′h′
Substituting the values:
P=13,600kg/m3⋅14.7m/s2⋅0.51m
Calculating this gives:
P≈101,325Pa (or 1 atm)
The air pressure in the elevator when it is accelerating upwards at 4.9m/s2 is approximately 101,325Pa.
Topper's Solved these Questions
Similar Questions
A barometer kept in an alevator ac celerating upward reads 76 cm of mrecury. If the elevator is ac celerating upwards at 4.5ms−2 find the air pressure in the elevator in cm of mercury. Density of mercuty =13.6×103kgm−3G=9.8m/s2
View SolutionA barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
View Solution
Knowledge Check
A barometer kept in a stationary elevator reads 76cm. If the element starts accelerating up the reading will be
AZeroBEqual to 76cmCMore than 76cmDLess than 76cm
A barometer is kept in an elevator accelerating upwards at 4.9m/s2. If the barometer reads 77 cm of Hg, what will be the air pressure in the elevator?
View SolutionA barometer accelerating downwards reads 76 cm of Hg. What will be the possible air pressure inside the jar?
View SolutionA barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be
View SolutionAn elevator is accelerating downwards with an acceleration of 4.9 ms−2. A barometer placed in this elevator reads 75 cm of Hg. Calculate the air pressure inside the elevator.
View SolutionA person in an elevator accelerating upwards with an acceleration of 2ms−2 , tosses a coin vertically upwards with a speed of 20ms−1 . After how much time will the coin fall back into his hand ? (g = 10 ms−2)
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
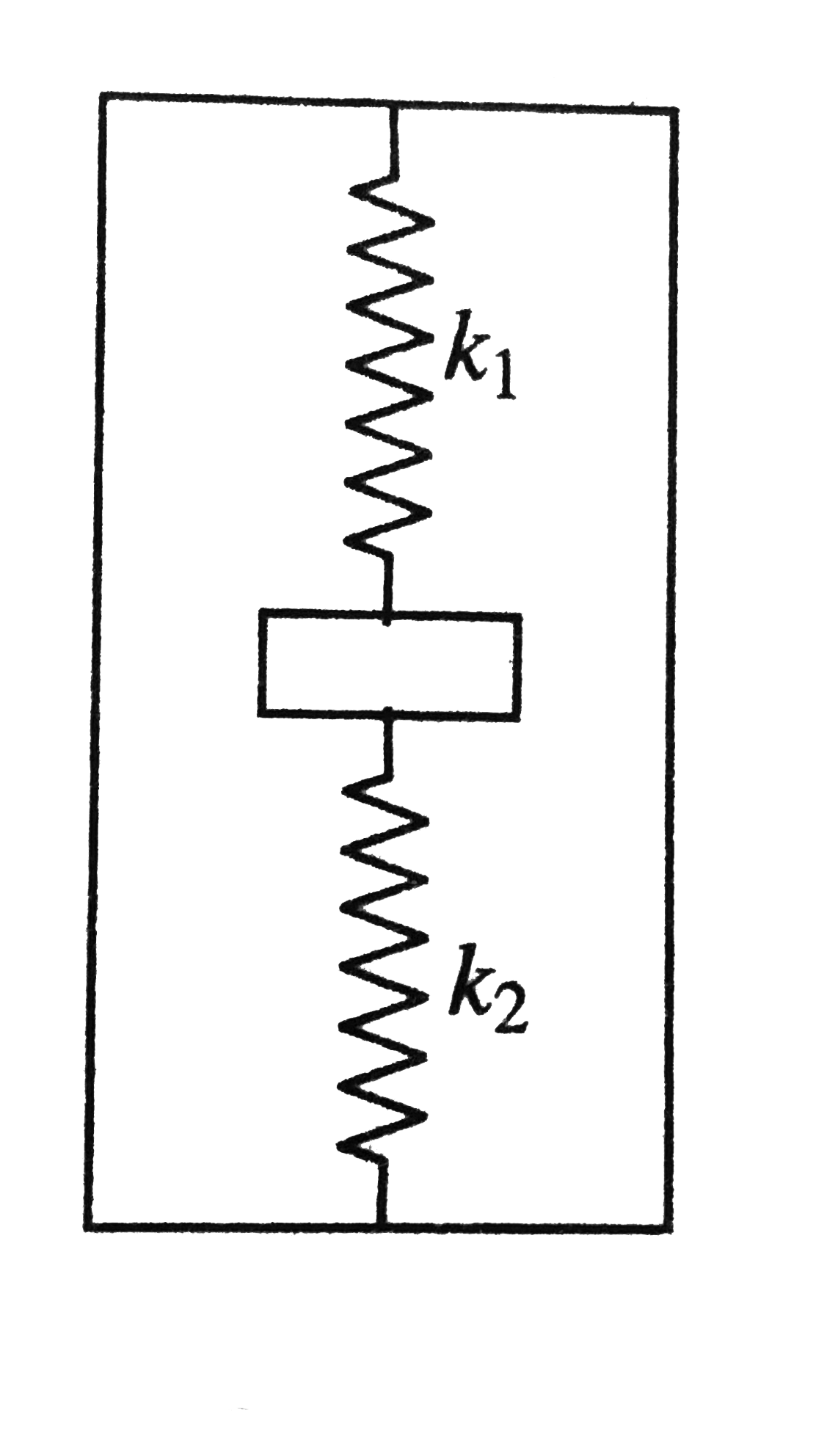
View SolutionA person in an elevator accelerating upwards with an acceleration of 2ms−2 , tosses a coin vertically upwards with a speed of 20ms−1 . After how much time will the coin fall back into his hand ? (g = 10 ms−2)
View Solution
