A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
To solve the problem of determining the impulse imparted to the ball when a batsman hits it back, we can follow these steps:
Step 1: Understand the concept of impulse
Impulse is defined as the change in momentum of an object. Mathematically, it can be expressed as:
Impulse=Δp=pfinal−pinitial
where p is the momentum.
Step 2: Identify the given values
From the problem, we have:
- Mass of the ball, m=0.15kg
- Initial speed of the ball, vi=12m/s (in the positive direction)
- Final speed of the ball after being hit back, vf=−12m/s (in the negative direction)
Step 3: Calculate the initial momentum
The initial momentum pinitial of the ball can be calculated using the formula:
pinitial=m⋅vi
Substituting the values:
pinitial=0.15kg⋅12m/s=1.8kg m/s
Step 4: Calculate the final momentum
The final momentum pfinal of the ball after being hit back can be calculated using the formula:
pfinal=m⋅vf
Substituting the values:
pfinal=0.15kg⋅(−12m/s)=−1.8kg m/s
Step 5: Calculate the impulse
Now, we can find the impulse by substituting the values of pfinal and pinitial into the impulse formula:
Impulse=pfinal−pinitial
Substituting the calculated momenta:
Impulse=(−1.8kg m/s)−(1.8kg m/s)=−3.6kg m/s
Step 6: Determine the magnitude of impulse
Since impulse is a vector quantity, we can take the magnitude:
Magnitude of Impulse=|−3.6kg m/s|=3.6kg m/s
Final Answer
The impulse imparted to the ball is 3.6kg m/s.
---
Impulse is defined as the change in momentum of an object. Mathematically, it can be expressed as:
Impulse=Δp=pfinal−pinitial
where p is the momentum.
From the problem, we have:
- Mass of the ball, m=0.15kg
- Initial speed of the ball, vi=12m/s (in the positive direction)
- Final speed of the ball after being hit back, vf=−12m/s (in the negative direction)
The initial momentum pinitial of the ball can be calculated using the formula:
pinitial=m⋅vi
Substituting the values:
pinitial=0.15kg⋅12m/s=1.8kg m/s
The final momentum pfinal of the ball after being hit back can be calculated using the formula:
pfinal=m⋅vf
Substituting the values:
pfinal=0.15kg⋅(−12m/s)=−1.8kg m/s
Now, we can find the impulse by substituting the values of pfinal and pinitial into the impulse formula:
Impulse=pfinal−pinitial
Substituting the calculated momenta:
Impulse=(−1.8kg m/s)−(1.8kg m/s)=−3.6kg m/s
Since impulse is a vector quantity, we can take the magnitude:
Magnitude of Impulse=|−3.6kg m/s|=3.6kg m/s
The impulse imparted to the ball is 3.6kg m/s.
Similar Questions
Knowledge Check
Two billiard ball A and B each of mass 50g and moving in opposite direction with speed of 5ms−1 each, collide and rebound with the same speed. The impulse imparted to each ball is
A0.25kgms−1B0.5kgms−1C0.8kgms−1D0.125kgms−1
A batsman deflects a ball by an angle of 45∘ without changing its initial speed which is equal to 54kmh. What is the impulse imparted to the ball ? (Mass of the ball is 0.15 kg)
View SolutionA batsman deflects a ball by an angle of 90∘ without changing its initial speed, which is equal to 54 km/hr. What is the impulse to the ball ? Mass of the ball is 0.15 kg.
View SolutionA bowler tbrows a ball horizontally along east direction with speed of 144km/hr. The batsman hits the ball such that it deviates from its initial direction of motion by 74∘ north of east direction, without changing its speed. If mass of the ball is 13kg and time of contact between bat and ball is 0.02 s. Average force applied by batsman on ball is:
A. 800 N, 53∘East of North
B. 800N, 53∘ North of East
C. 800 N, 53∘ North of West
D. 800N, 53∘ West of North
View SolutionCalculate the de Broglie wavelength of a ball of mass 0.1kg moving with a speed of 30ms−1
View SolutionA hockey player receives a corner shot at a speed of 15m/s at an angle of 30∘ with the y-axis and then shoots the ball along the x-axis with a speed of 30m/s If the mass of the ball is 150gm and it remains in contact with the hockey stick for 0.01s, the force imparted to the ball in the x-direction is :
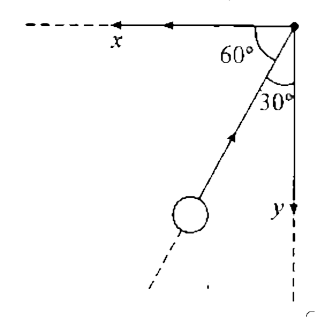
View SolutionTwo billiard balls each of mass 0.05 kg moving in opposite directions with speed 6ms−1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other ?
View SolutionAs shown in fig. two identical balls strike a rigid wall with equal speeds but a different angles of incidence. They are reflected back without any lose in speed.


(a) Determine the direction of force exerted by each ball on the wall.
(b) Determine the ratio of impulse imparted by the two balls on the wall in both cases.
View Solution
