A bowler tbrows a ball horizontally along east direction with speed of 144km/hr. The batsman hits the ball such that it deviates from its initial direction of motion by 74∘ north of east direction, without changing its speed. If mass of the ball is 13kg and time of contact between bat and ball is 0.02 s. Average force applied by batsman on ball is:
A. 800 N, 53∘East of North
B. 800N, 53∘ North of East
C. 800 N, 53∘ North of West
D. 800N, 53∘ West of North
800 N, 53∘East of North
800N, 53∘ North of East
800 N, 53∘ North of West
800N, 53∘ West of North
The correct Answer is:C
To solve the problem, we need to find the average force applied by the batsman on the ball. We will follow these steps:
Step 1: Convert the speed of the ball from km/hr to m/s
The speed of the ball is given as 144 km/hr. To convert this to m/s, we use the conversion factor 518.
V1=144×518=40m/s
Step 2: Determine the final velocity vector after the batsman hits the ball
The batsman hits the ball such that it deviates by 74∘ north of east. The final velocity V2 remains the same in magnitude as V1, which is 40 m/s.
Step 3: Calculate the change in velocity
We need to find the change in velocity ΔV. The initial velocity vector V1 can be represented as:
V1=40^i(east direction)
The final velocity vector V2 can be represented using trigonometric components:
V2=40cos(74∘)^i+40sin(74∘)^j
Calculating the components:
V2=40cos(74∘)^i+40sin(74∘)^j
Using cos(74∘)≈0.2756 and sin(74∘)≈0.9613:
V2≈40×0.2756^i+40×0.9613^j≈11.024^i+38.452^j
Step 4: Calculate the change in velocity vector
The change in velocity ΔV is given by:
ΔV=V2−V1=(11.024^i+38.452^j)−(40^i)=(−28.976^i+38.452^j)
Step 5: Calculate the magnitude of the change in velocity
The magnitude of the change in velocity is given by:
|ΔV|=√(−28.976)2+(38.452)2
Calculating this:
|ΔV|=√839.4+1474.5=√2313.9≈48.1m/s
Step 6: Calculate the change in momentum
The change in momentum Δp is given by:
Δp=m⋅ΔV
Given that the mass m=13kg:
Δp=13⋅48.1≈16.03kg m/s
Step 7: Calculate the average force
The average force F is given by:
F=ΔpΔt
Given Δt=0.02s:
F=16.030.02≈801.5N≈800N
Step 8: Determine the direction of the force
To find the direction of the force, we can use the components of the change in velocity:
tan(θ)=38.45228.976
Calculating θ:
θ=tan−1(38.45228.976)≈53∘
Thus, the direction of the average force is 53∘ north of west.
Final Answer
The average force applied by the batsman on the ball is approximately 800N at 53∘ north of west.
---
The speed of the ball is given as 144 km/hr. To convert this to m/s, we use the conversion factor 518.
The batsman hits the ball such that it deviates by 74∘ north of east. The final velocity V2 remains the same in magnitude as V1, which is 40 m/s.
We need to find the change in velocity ΔV. The initial velocity vector V1 can be represented as:
The change in velocity ΔV is given by:
The magnitude of the change in velocity is given by:
The change in momentum Δp is given by:
The average force F is given by:
To find the direction of the force, we can use the components of the change in velocity:
The average force applied by the batsman on the ball is approximately 800N at 53∘ north of west.
Similar Questions
A rubber ball of mass 0.4 kg hits the ground at same angle without any change in speed . If the speed of ball is 1 m/s and the period of contact between the ball and floor is 0.4 s, find the average force exerted by the ball on the ground .
View SolutionA batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12ms−1 . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
View Solution
Knowledge Check
A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12ms−1 . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
A1.8N sB2.8N sC3.6N sD4.2N s
A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12ms−1 . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
View SolutionA ball reaches a racket at 60m/s along +X direction and leaves the racket in the opposite direction with the same speed. Assuming that the mass of the ball as 50gm and the contact time is 0.02 second the force exerted by the racket on the ball is .
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
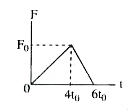
Average force exerted by the bat on the ball is
View SolutionA car is moving in east direction. It takes a right turn and moves along south direction without change in its speed. What is the direction of average acceleration of the car?
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA cricket ball of mass 150 g is moving with a speed of 12ms−1 and is hit by a bat so that the ball is turned back with velocity of 20ms−1 if duration of contact between bat and ball is 0.01 s then:

View Solution
