A battery of e.m.f 6 V and internal resistance 1Ω gives a p.d of 5.8 V when connected to a resistance . Find the external resistance .
To solve the problem step by step, we will use the information provided in the question and apply Ohm's law and the concept of internal resistance in a circuit.
1. Identify the given values:
- Electromotive force (e) = 6 V
- Internal resistance (r) = 1 Ω
- Potential difference across the terminals (V) = 5.8 V
2. Apply the formula for potential difference:
The relationship between the electromotive force, potential difference, internal resistance, and external resistance is given by:
e=V+i⋅r
where i is the current flowing through the circuit.
3. Express the current (i):
The current can be expressed in terms of the external resistance (R) using Ohm's law:
i=eR+r
Substituting the values we have:
i=6R+1
4. Substitute the current into the potential difference equation:
Now, we substitute i into the equation for potential difference:
V=e−i⋅r
This gives us:
5.8=6−(6R+1)⋅1
5. Rearrange the equation:
Rearranging the equation, we have:
5.8=6−6R+1
This simplifies to:
6R+1=6−5.8
6R+1=0.2
6. Cross-multiply to solve for R:
Cross-multiplying gives:
6=0.2(R+1)
Expanding this, we have:
6=0.2R+0.2
7. Isolate R:
Now, subtract 0.2 from both sides:
6−0.2=0.2R
5.8=0.2R
Dividing both sides by 0.2 gives:
R=5.80.2=29Ω
8. Conclusion:
The external resistance R is therefore:
R=29Ω
- Electromotive force (e) = 6 V
- Internal resistance (r) = 1 Ω
- Potential difference across the terminals (V) = 5.8 V
The relationship between the electromotive force, potential difference, internal resistance, and external resistance is given by:
e=V+i⋅r
where i is the current flowing through the circuit.
The current can be expressed in terms of the external resistance (R) using Ohm's law:
i=eR+r
Substituting the values we have:
i=6R+1
Now, we substitute i into the equation for potential difference:
V=e−i⋅r
This gives us:
5.8=6−(6R+1)⋅1
Rearranging the equation, we have:
5.8=6−6R+1
This simplifies to:
6R+1=6−5.8
6R+1=0.2
Cross-multiplying gives:
6=0.2(R+1)
Expanding this, we have:
6=0.2R+0.2
Now, subtract 0.2 from both sides:
6−0.2=0.2R
5.8=0.2R
Dividing both sides by 0.2 gives:
R=5.80.2=29Ω
The external resistance R is therefore:
R=29Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
12 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
12 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
The potential difference between the terminals of a battery of emf 6.0V and internal resistance1(Ω)drops to 5.8 V when connected across an external resistor. Find the resistance of the external resistor.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionIn the circuit shown below, E is a battery of emf 6 V and internal resistance 1Ω. Find the reading of the ammeter A. if it has negligible resistance :
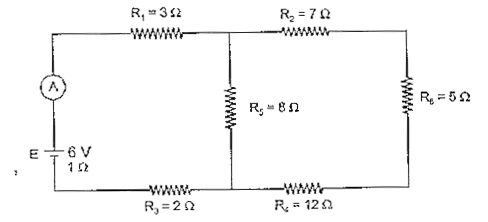
View SolutionA battery of e.m.f. 15 V and internal resistance 2 Ω is connected to two resistors of resistances 4 ohm and 6 ohm joined in series. Find the electrical energy spent per minute in 6 ohm resistor.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the p.d. between the terminals of the battery,
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
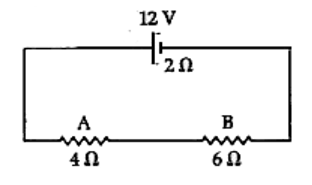
Find The potential difference across 6 Ω Resistor.
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View Solution