A battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the components and their values
- E.M.F of the battery (V) = 15 V
- Internal resistance of the battery (r) = 3 Ω
- Resistor 1 (R1) = 3 Ω
- Resistor 2 (R2) = 6 Ω
Step 2: Calculate the equivalent resistance of the resistors in parallel
The formula for the equivalent resistance (R') of two resistors in parallel is given by:
1R′=1R1+1R2
Substituting the values:
1R′=13+16
Step 3: Find a common denominator and simplify
The least common multiple (LCM) of 3 and 6 is 6. Therefore, we can rewrite the fractions:
1R′=26+16=36
Thus, we can find R':
R′=63=2Ω
Step 4: Calculate the total resistance in the circuit
The total resistance (R_total) in the circuit is the sum of the internal resistance of the battery and the equivalent resistance of the parallel resistors:
Rtotal=R′+r=2Ω+3Ω=5Ω
Step 5: Use Ohm's Law to find the current through the battery
Ohm's Law states that:
V=I×R
Rearranging this to find the current (I):
I=VRtotal
Substituting the values:
I=15V5Ω=3A
Final Answer
The current through the battery is 3 A.
---
- E.M.F of the battery (V) = 15 V
- Internal resistance of the battery (r) = 3 Ω
- Resistor 1 (R1) = 3 Ω
- Resistor 2 (R2) = 6 Ω
The formula for the equivalent resistance (R') of two resistors in parallel is given by:
1R′=1R1+1R2
Substituting the values:
1R′=13+16
The least common multiple (LCM) of 3 and 6 is 6. Therefore, we can rewrite the fractions:
1R′=26+16=36
Thus, we can find R':
R′=63=2Ω
The total resistance (R_total) in the circuit is the sum of the internal resistance of the battery and the equivalent resistance of the parallel resistors:
Rtotal=R′+r=2Ω+3Ω=5Ω
Ohm's Law states that:
V=I×R
Rearranging this to find the current (I):
I=VRtotal
Substituting the values:
I=15V5Ω=3A
The current through the battery is 3 A.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C)
22 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C) MULTIPLE CHOICE TYPE)
2 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (MULTIPLE CHOICE TYPE)
3 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
A battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the p.d. between the terminals of the battery,
View SolutionA battery of e.m.f. 15 V and internal resistance 2 Ω is connected to two resistors of resistances 4 ohm and 6 ohm joined in series. Find the electrical energy spent per minute in 6 ohm resistor.
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
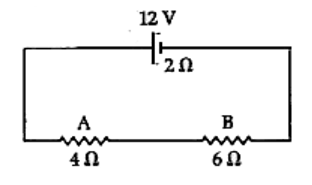
Find The potential difference across 6 Ω Resistor.
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
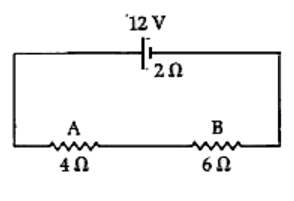
Find Electrical energy spent per minute in 4 Ω Resistor.
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the current in the circuit,
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the voltage drop when the current is flowing.
View SolutionIn the circuit diagram given below, a cell of 9 V and internal resistance of 0.5(Ω) is connected across a resistor A of 2Ω in series and two resistors of 2Ω and 6Ω in parallel.
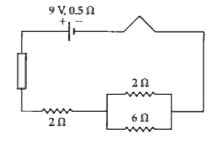
Find
The current in the 6Ω resistor.
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View Solution
