A belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
3.2rad/s
0.32rad/s
20rad/s
0.032rad/s
The correct Answer is:C
To find the angular velocity of the belt moving over a wheel, we can follow these steps:
1. Identify the Given Values:
- Radius of the wheel (r) = 25 cm = 0.25 m (convert to meters for consistency)
- Speed of the point on the belt (v) = 5 m/s
2. Use the Relationship Between Linear Speed and Angular Velocity:
The relationship between linear speed (v) and angular velocity (ω) is given by the formula:
v=ω⋅r
where:
- v is the linear speed,
- ω is the angular velocity in radians per second,
- r is the radius of the wheel.
3. Rearrange the Formula to Solve for Angular Velocity (ω):
To find the angular velocity, we can rearrange the formula:
ω=vr
4. Substitute the Known Values into the Equation:
Now, substitute the values of v and r:
ω=5m/s0.25m
5. Calculate the Angular Velocity:
ω=50.25=20radians/second
Final Answer:
The angular velocity of the belt is ω=20radians/second.
- Radius of the wheel (r) = 25 cm = 0.25 m (convert to meters for consistency)
- Speed of the point on the belt (v) = 5 m/s
The relationship between linear speed (v) and angular velocity (ω) is given by the formula:
v=ω⋅r
where:
- v is the linear speed,
- ω is the angular velocity in radians per second,
- r is the radius of the wheel.
To find the angular velocity, we can rearrange the formula:
ω=vr
Now, substitute the values of v and r:
ω=5m/s0.25m
ω=50.25=20radians/second
The angular velocity of the belt is ω=20radians/second.
Topper's Solved these Questions
Similar Questions
Calculate the angular speed of againt wheel of radius 10 m, moving with a speed of 10m/s.
View SolutionAn elastic belt is placed round the rim of a pulled of radius 5cm. One point on the belt is pulled directly away from the centre O of the pulley until it is at P, 10cm from O. Find the length of the belt that is in contact with the rim of the pulley. Also, find the shaded area.
View Solution
Knowledge Check
A strap is passing over a wheel of radius 30 cm. During the time the wheel moving with initial constant velocity of 2 rev/sec. comes to rest the strap covers a distance of 25 m. The deceleration of the wheel in rad/s is
A0.94B1.2C2.0D2.5A particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
A500radsB150radsC50radsD15radsSand is being dropped on a conveyor belt at the rate of Mkg/s . The force necessary to kept the belt moving with a constant with a constant velocity of vm/s will be.
AMv newtonB2 Mv newtonCMv2 newtonDzero
An elastic belt is placed around the rim of a pulley of radius 5 cm (Fig.) From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also, find the shaded area.[use π=3.14 and √3=1.73]
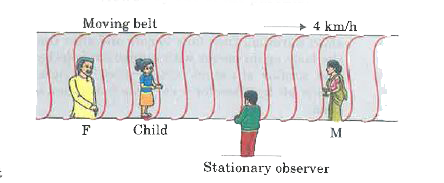
View SolutionOna long horizontally moving belt, a child runs to and fro with a speed 9 km h−1 (with respect to the belt) between his father and mother located 50m apart on the moving belt. The belt moves with a speed on the moving belt. The belt moves with a speed of 4 km h−1. for an observer on a stationary platform outside, what is the
(a) Speed of the child running in the direction of motion of the belt?
(b) speed of the child running opposite to the direction of motion of the belt?
(c ) time taken by the child in a and b?
which of the answers after if motion is viewed by one of the parents?
View SolutionWheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]

View SolutionTwo wheels are connected by a belt.The radius of larger wheel is three times that of the smaller one.What is the ratio of the angular velocity of the two wheels i.e.ωbωs ?
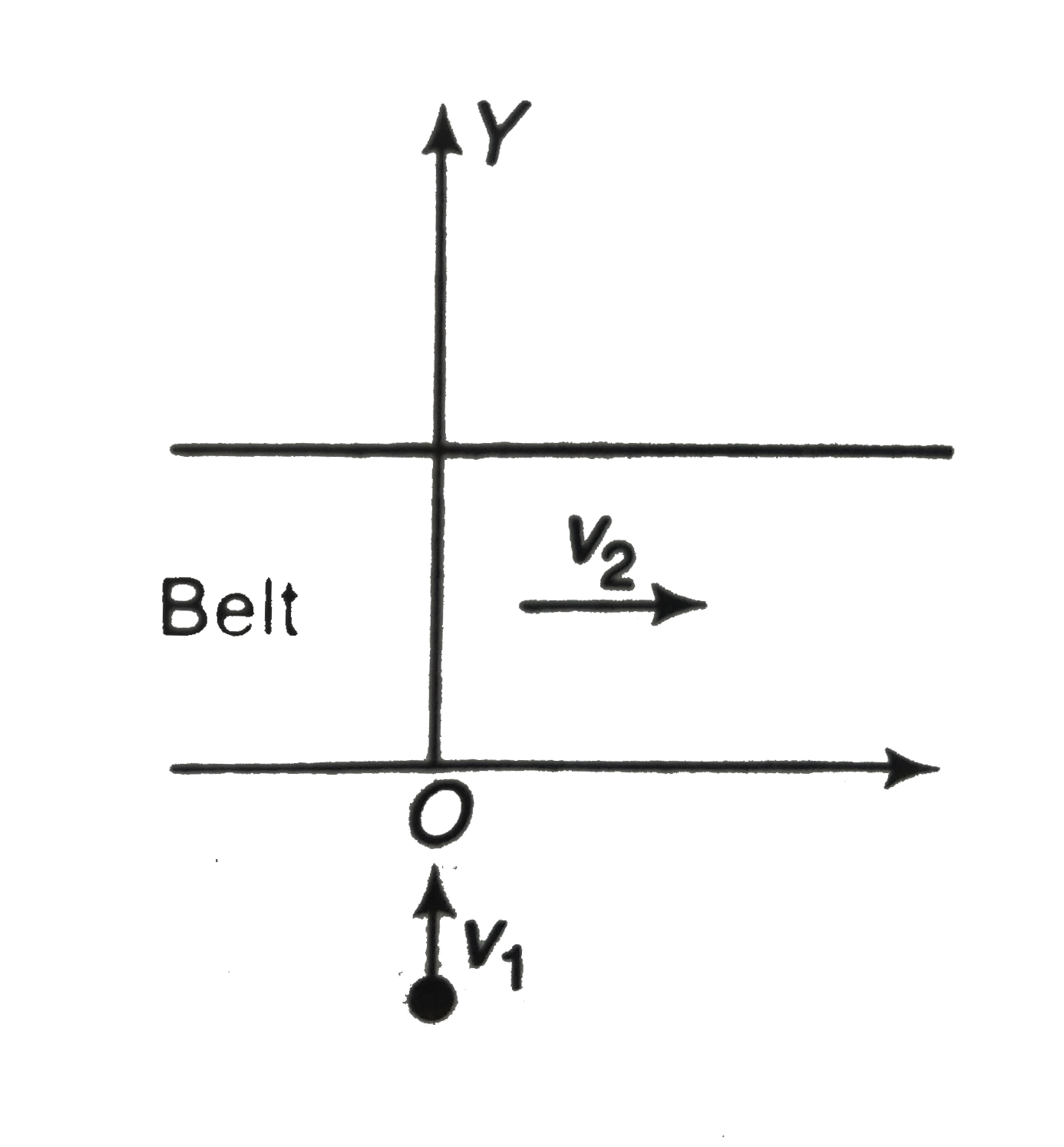
View SolutionA partical of mass m and velocity v1 in positive y direction is projected on to a belt that is moving with uniform velocity v2 in x- direction as shown in figure. Coefficient of friction between partical and belt is μ . Assuming that the partical first touches the belt at the origin of fixed x−y coordinate system and remains on the belt , find co-ordinates (x−y) of the point where slidding stop.
View Solution
