A partical of mass m and velocity v1 in positive y direction is projected on to a belt that is moving with uniform velocity v2 in x- direction as shown in figure. Coefficient of friction between partical and belt is μ . Assuming that the partical first touches the belt at the origin of fixed x−y coordinate system and remains on the belt , find co-ordinates (x−y) of the point where slidding stop.
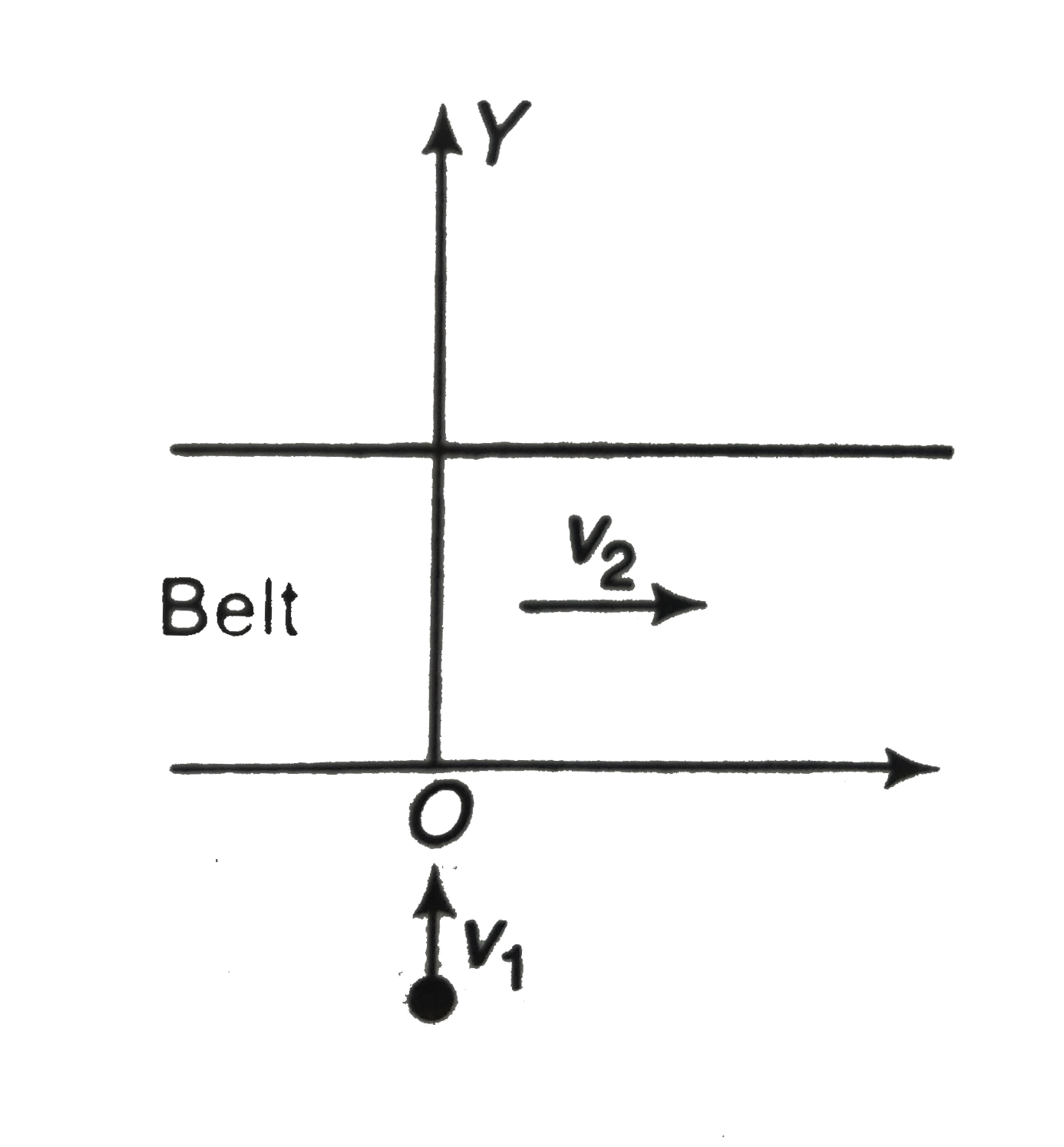
vr=√v21+v22
Reterdation a=μg
∴ Time when slipping stop is t=vra
or t=√v21+v22μg
sr=v2r2a=v21+v222μg
xr=−sr,cosθ=−(v21+v222μg)⎛⎜
⎜⎝v2√v21+v22⎞⎟
⎟⎠
−v2√v21+v222μg
yr=srsinθ=(v21+v222μg)⎛⎜
⎜⎝v1√v21+v22⎞⎟
⎟⎠<br>= (v_(1)sqrt (v_(1)^(2) + v_(2)^(2)))/(2 mu g)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V01_C08_E01_198_S01.pngwh=80%mx-autosty≤=background:white;><br>Intimetbe<willmoveadistances = v_(2) t<br>orv_(2)sqrt (v_(1)^(2)) + v_(2)^(2))/( mu g)∈x−direction<br>Hence,c∞rd∈ateofpartic≤,<br>x = x_(r) + s = v_(2)sqrt (v_(1)^(2) + v_(2)^(2))/( 2 mu g)<br>andy = y_(r) = v_(1)sqrt (v_(1)^(2)) + v_(2)^(2))/( 2 mu g)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - example
86 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.1
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
View SolutionWith what minimum velocity should be projected from left end A toward end B such that it reaches the other end B of conveyer belt moving with constant velocity v The friction coefficient between block and belt is μ
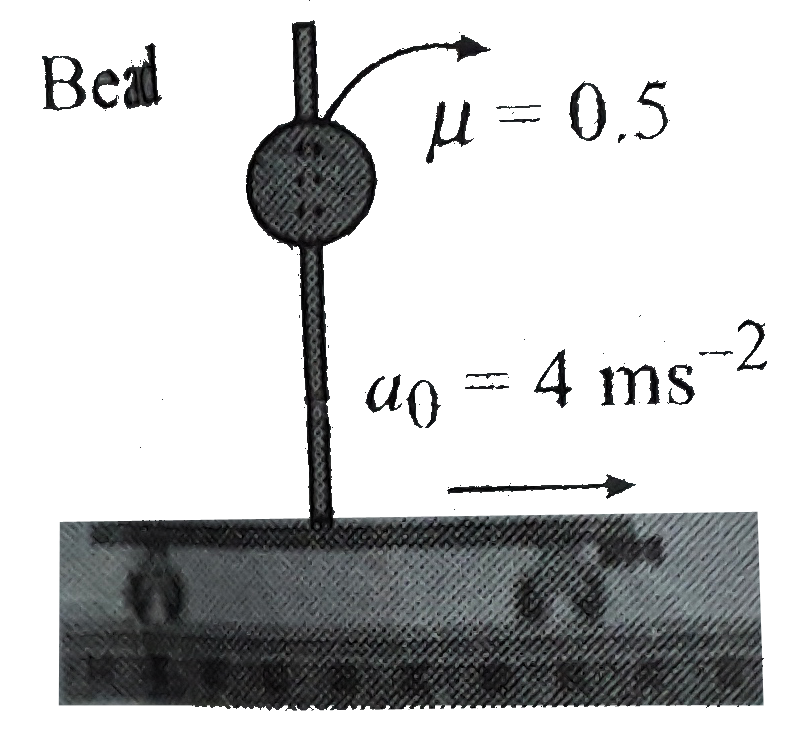
View Solution
Knowledge Check
A particle is projected with a speed v0=√gR. The coefficient of friction the particle and the hemi- spherical plane is μ=0.5 Then , the acceleration of the partical is
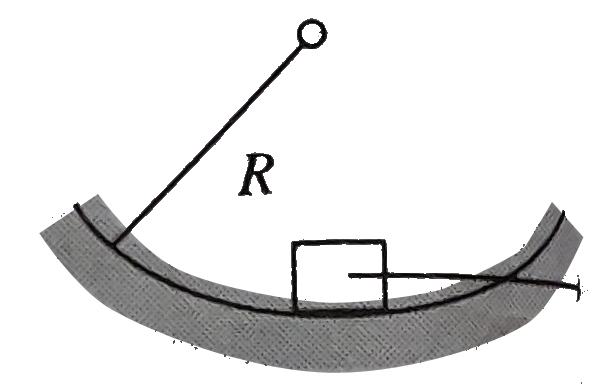 AgB√5g2C√2gDnone of these
AgB√5g2C√2gDnone of theseHot belt is known as
AEquatorial regionBSavanna regionCDry and wet regionDMediterranean regionA belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
A3.2rad/sB0.32rad/sC20rad/sD0.032rad/s
A charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionWhere is the asteroid belt located?
View SolutionA conveyed belt of length lis moving with velocity v.a block of mass is pushed against the motion of conveyed belt with velocity v0 form end B Co- efficient of friction between block and belt is u the value of v0 so that the amount of heat liberated as a result of retardation of the block by conveyed belt is maximum is
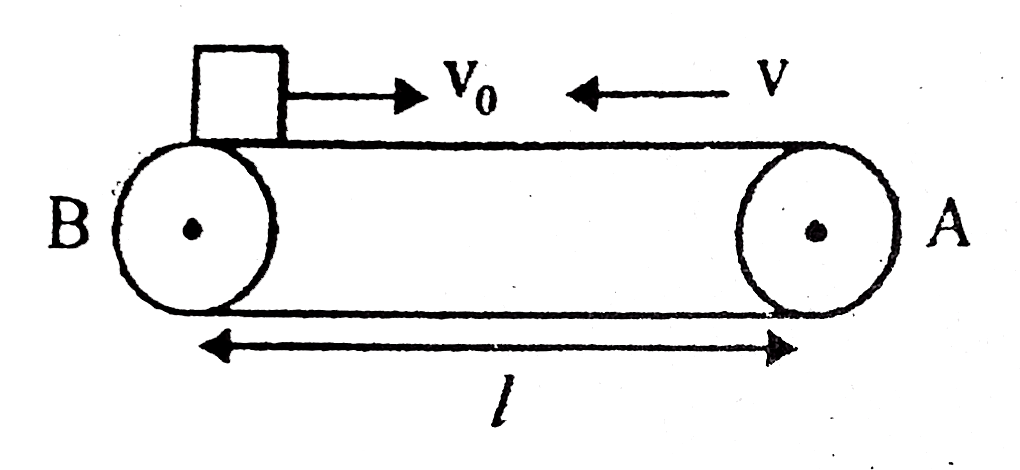
View Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
View SolutionA partical is placed at rest inside a hollow hemisphare of redius R. The coefficient of friction between the partical and the homisphere is μ=1√3. The maximum height up to which the partical can remain stationary is
View Solution