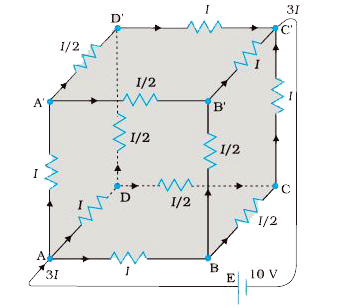
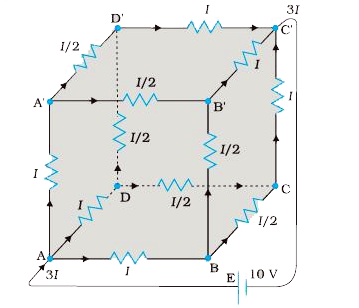
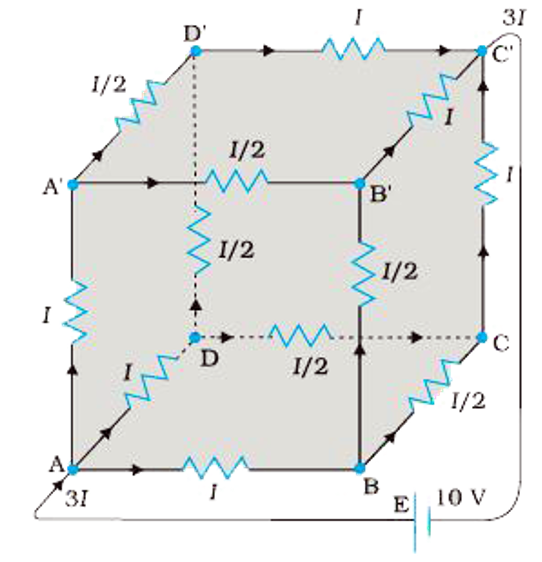
A bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
 Solution in Gujrati
Solution in Gujrati
Above cubical network ls shown as per the statement, where each of 12 identical sides, is a resistor of resistance R = 1 Ω. We have to find equivalent resistance of this network between its diagonally opposite points, say between points A and G in above figure. For this purpose, connect a battery across these two points.
Now, current I starting from positive terminal of battery reaches point A, after which it is offered three branches AB, AD and AE and so it is divided into three parts. Here, minimum resistance offered to each of these three parts to reach negative terminal of battery is same and so all of these three parts are equal. Hence, each part wouJd be I/3. Thus, current arriving at points E, D and B are all I/3. These all currents are further divided into two parts as all of them are further offered two branches after points B, D and E. Here, minimum resistance offered to each of these two parts to reach negative terminal of battery is same and so each 1/3 amount of current gets divided into two equal parts after coming to points B, D and E. Hence, currents passing through BC and BF, DC and DH, EF and EH are all
I32=16 .
Now, at each of the junctions C, F and H, two cu.rrents each of amount 1/6 add up to give 1/3 amount of current, which flow in the branches CG, FG and HG respectively. These three cu.rrents each of amount 1/3 associate at exit point G to give total current I which is equal to current at the entry point A of given cubical network..
Now, applying KVL (Kirchhoff.s Voltage Law) in the direction of current along the closed path AEHGJKA we get,
- (I3)(R)−(I6)(R)−(I3)(R)=−ε
∴ε=IR3+IR6+IR3
∴ε=5IR6 ... (1)
Now, if equivalent resistance of given cubical network between its diagonally opposite end points is Req, then
Req=εI=5R6 [ From equation (1) ] ... (2)
Here R = 1 Ω and so : Req=56Ω
From equation (1) ,
10=5I×16
∴I=12A
Current through branches AB, AD, AE, CG, FG, HG is , I3=123=4 A
Current through branches BC, BF, DC, DH, EF, EH is , I6=126=2 A
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [B] (NUMERICAL FROM TEXTUAL EXERCISE)35videos
CURRENT ELECTRICITY
- BOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [B] (NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK)13videos
CURRENT ELECTRICITY
- BOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [A] TRY YOURSELF74videos
CURRENT ELECTRICITY
- BOOK - KUMAR PRAKASHANCHAPTER - BOARD'S QUESTION PAPER MARCH-2020 EXERCISE - PART-B SECTION -C4videos
BOARD'S QUESTION PAPER MARCH-2020
- BOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)1videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω , what is the maximum current that can be drawn from the battery ?
 04:23View Solution
04:23View SolutionThe current through a wire varies with time as I=I0+αt, where I0=10 A and α=4As−1 . The charge that flows across a cross-section of the wire in first 10 seconds is .....
08:00View SolutionWhat is reason behind producing electric force between two particles ?
09:03View SolutionDerive an expression for current I passing through an AC circuit containing only inductor L. Draw a Phasor diagram and graph of v and I versus ωt. Explain instantaneous power and the average power.
03:04View SolutionMass of photon in motion is ………
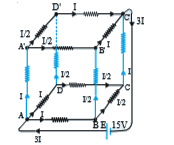
09:04View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
 07:49View Solution
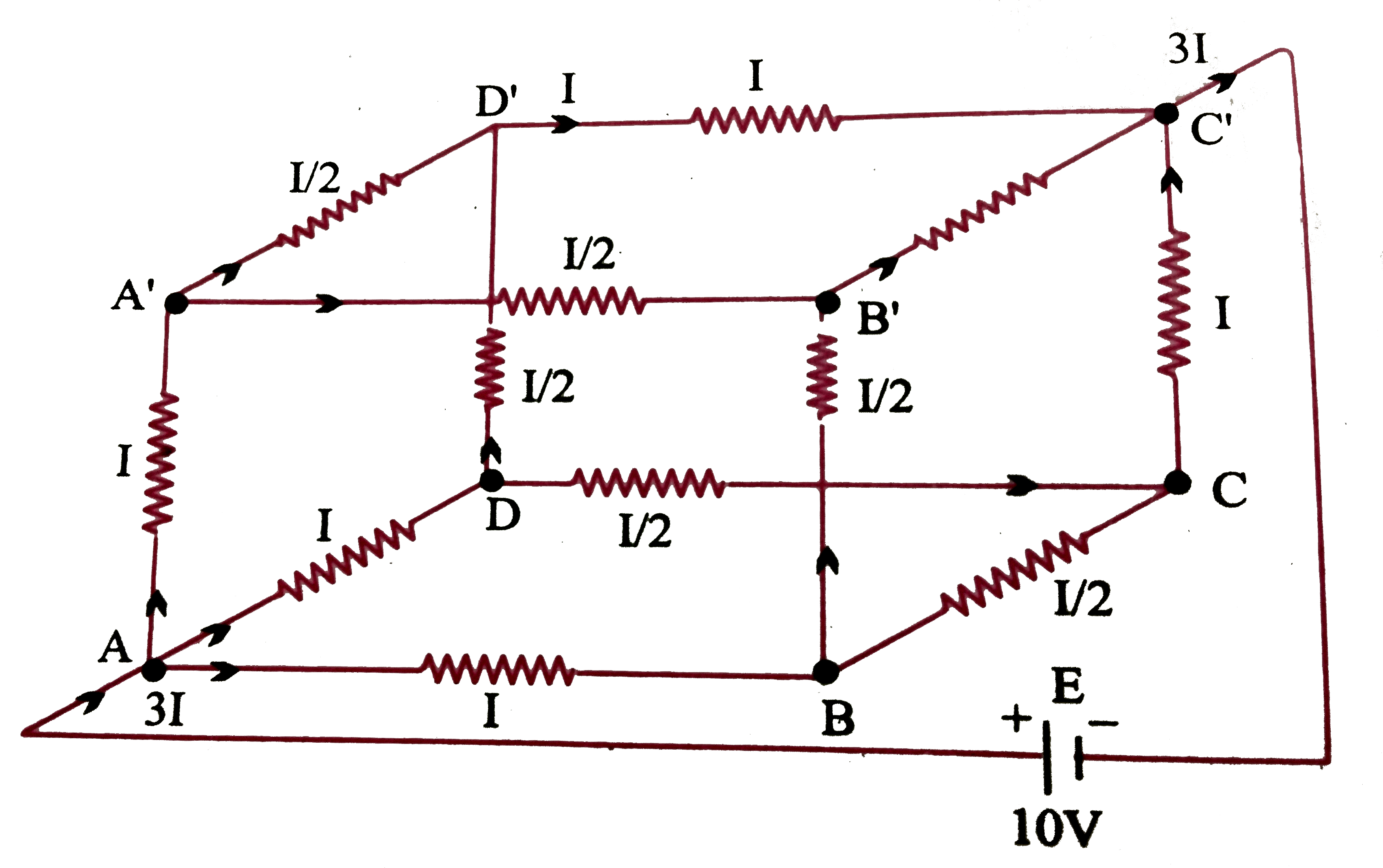
07:49View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1 Omega (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
04:42View Solution10 V तथा नगण्य आंतरिक प्रतिरोध की बैटरी एक घनीय परिपथ जाल ( नेटवर्क ) के "विकदत" सम्मुख कोनो से जुडी है परिपथ जाल में 1PΩ प्रतिरोध के 12 प्रतिरोधक है ( चित्र 3 .23 ) l परिपथ जाल का समतुल्य प्रतिरोध तथा धन के प्रत्येक के अनुदिश विधुत धारा ज्ञात कीजिए l
 04:23View Solution
04:23View SolutionA network of resistor is connected to a 16 V battery with internal resistance of 1 Omega , a shown in fig. (a) complete the equivalent resistance of the network.
06:45View Solution10 V तथा नगण्य आंतरिक प्रतिरोध कि बैटरी एक घनीय परिपथ जाल ( नेटवर्क ) के विकर्णताः सम्मुख कोनो से जुडी है । निम्न परिपथ जाल में 1Ω प्रतिरोध के 12 प्रतिरोधक है । परिपथ जाल का समतुल्य प्रतिरोध तथा घन के प्रत्येक किनारे के अनुदिश विद्युत धारा ज्ञात कीजिए ।
 05:02View Solution
05:02View SolutionTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
07:46View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Omega as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops V_(BC) and V_(CD)
05:51View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Omega 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
05:12View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
 05:46View Solution
05:46View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
 03:43View Solution
03:43View Solution

