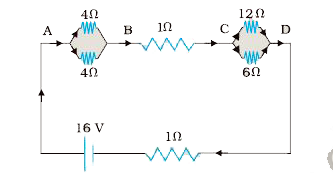
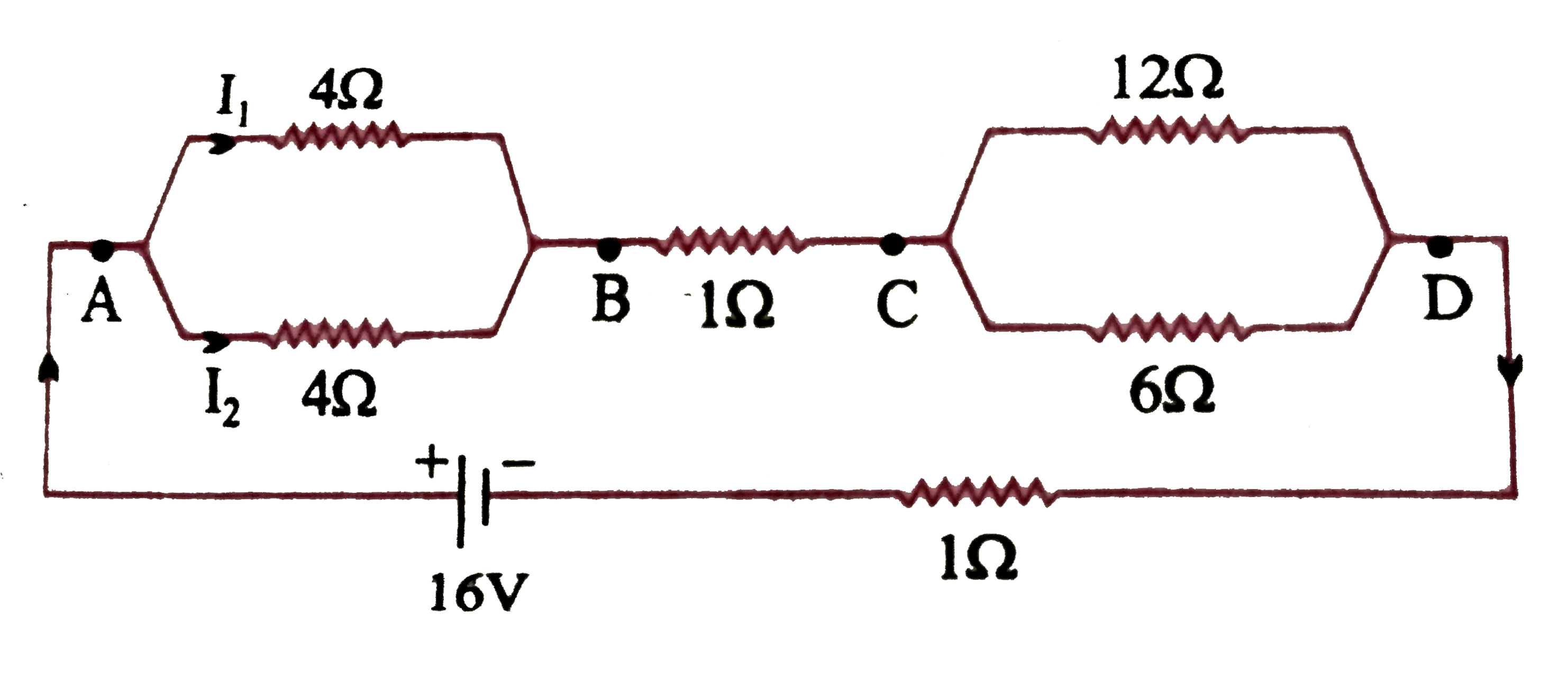
A network of resistore is connected to a 16 V battery with internal resistance of 1Ω, as shown in (a) Compute the equivalent resistance of the network. (b) Obtain the current in each resistor. (c ) obtain the voltage drops VAB,VBCandVCD
 Solution in Gujrati
Solution in Gujrati
(i) RAB=42=2Ω
(ii) RBC=1Ω
(iii) RCD=12×612+6=4Ω
Equivalent resistance of given network (between point A and D ) is,
R = RAD=RAB+RBC+RCD
= 2+1+4
∴=7Ω
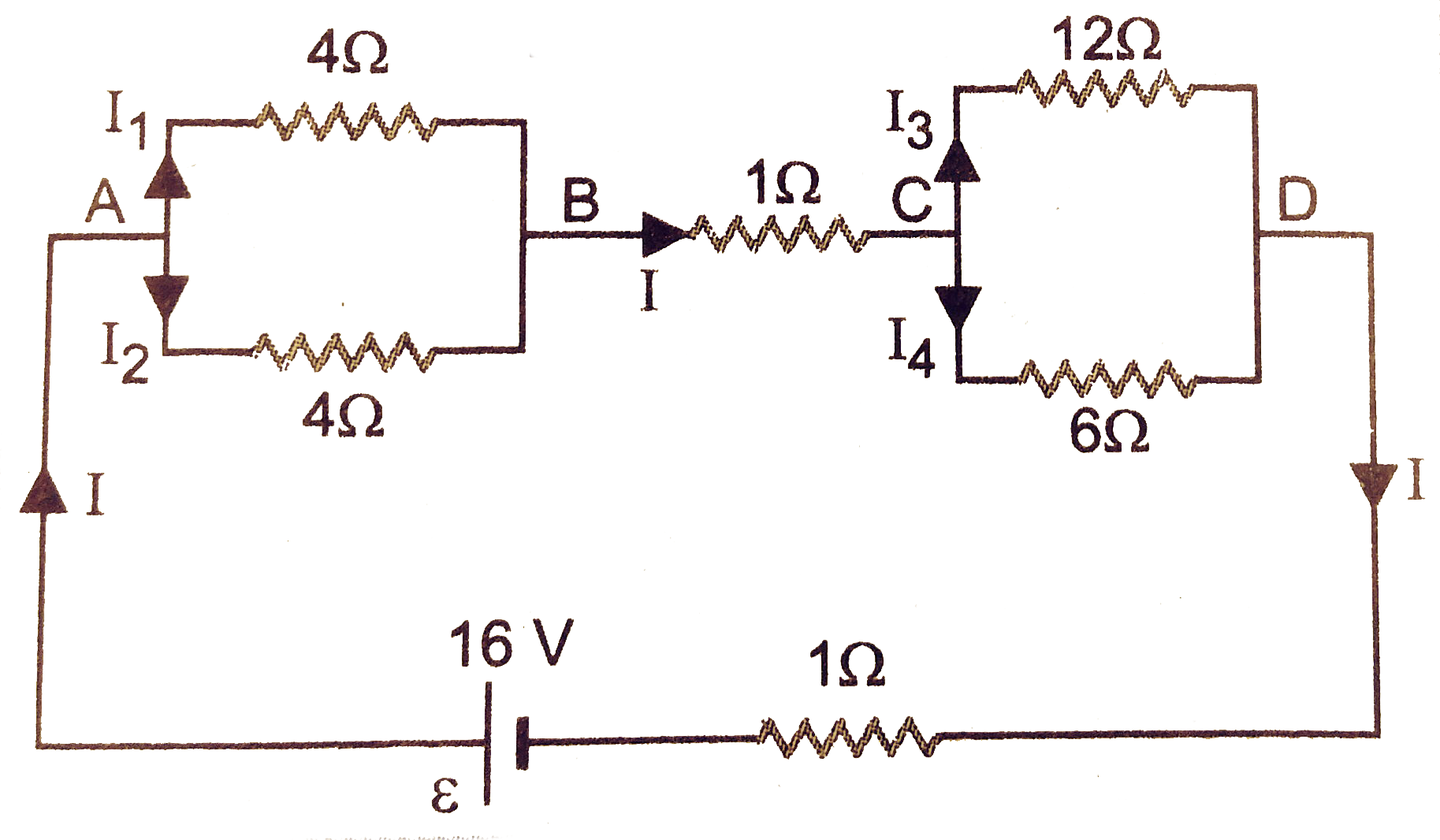
(b) Current passing through the battery is,
I=εR+r=167+1=2A
Between points A and B, two resistances each of 4Ω are connected in parallel and so potential difference (p.d.) across them should be equal . thus , I1×4=I2×4
⇒I1=I2
Now, I=I1+I2=2A⇒I1=I2=1A
Current through 1 Ω resistance is I = 2 A
Between point C and D , 12 Ωand6Ω resistances are connected in parallel and so
I3×12=I4×6
⇒I4=2I3
Now, I = I3+I4=I3+2I3=3I3=2A
(∵I=2A)
∴I3=23AandI4=2I3=43A
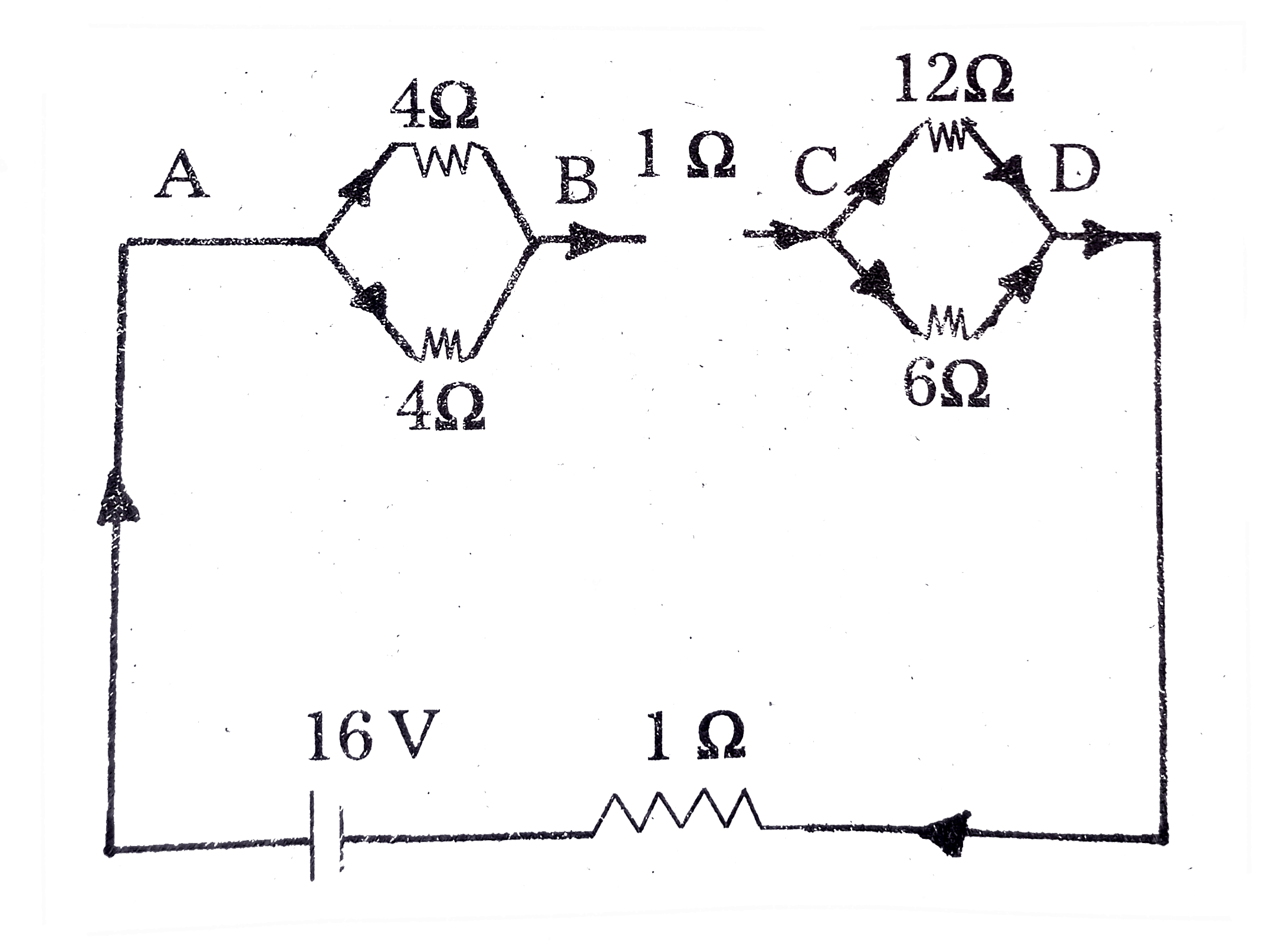
(C) VAB=I×RAB=2×2=4V
VBC=I×RBC=2×1=2V
VCD=I×RCD=2×4=8V
Note : Here, terminal voltage of given battery is,
V=VAB+VBC+VCD=4+2+8=14V
But emf of battery is ε=16 V
⇒ Remaining voltage drop = 16 - 14 = 2 V
is across internal resistance because
Ir =2 ×1=2V
Here, battery is getting discharged and so we get V = ε−Ir=16−(2)(I)=14 V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [B] (NUMERICAL FROM TEXTUAL EXERCISE)
35 Videos
- CURRENT ELECTRICITYBOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [B] (NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK)
13 Videos
- CURRENT ELECTRICITYBOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [A] TRY YOURSELF
74 Videos
- BOARD'S QUESTION PAPER MARCH-2020 BOOK - KUMAR PRAKASHANCHAPTER - BOARD'S QUESTION PAPER MARCH-2020 EXERCISE - PART-B SECTION -C
4 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)
1 Videos
Similar Questions
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω , what is the maximum current that can be drawn from the battery ?

View SolutionThe current through a wire varies with time as I=I0+αt, where I0=10 A and α=4As−1 . The charge that flows across a cross-section of the wire in first 10 seconds is .....
View SolutionWhat is reason behind producing electric force between two particles ?
View SolutionDerive an expression for current I passing through an AC circuit containing only inductor L. Draw a Phasor diagram and graph of v and I versus ωt. Explain instantaneous power and the average power.
View SolutionMass of photon in motion is ………
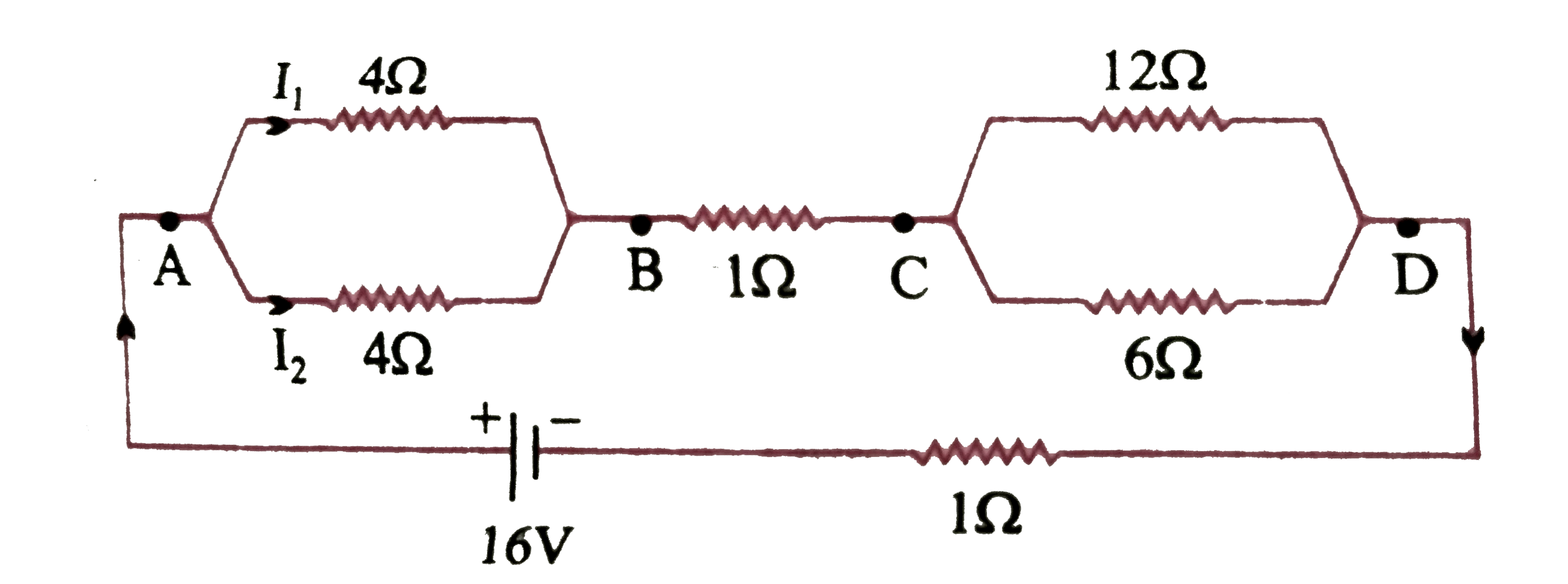
View SolutionA network of resistances is connected to a 16 V battery with internal resistance of 1Ω as shown in figure. (a) Compute the equivlaent resistance of the network. (b) Obtain the current in each resistor and (c ) obtain the voltage dropVAB,VBC and VCD.
View SolutionA network of resistances is connected to a 16 V battery with internal resistance of 1 Omega , as shown in Fig. 4.33. (a) Compute epuivalent resistance of the network, (b) obtain the current In in each resistor, and (c ) obtain the voltage drops V_(AB), V_(BC) " and " V_(CD) .
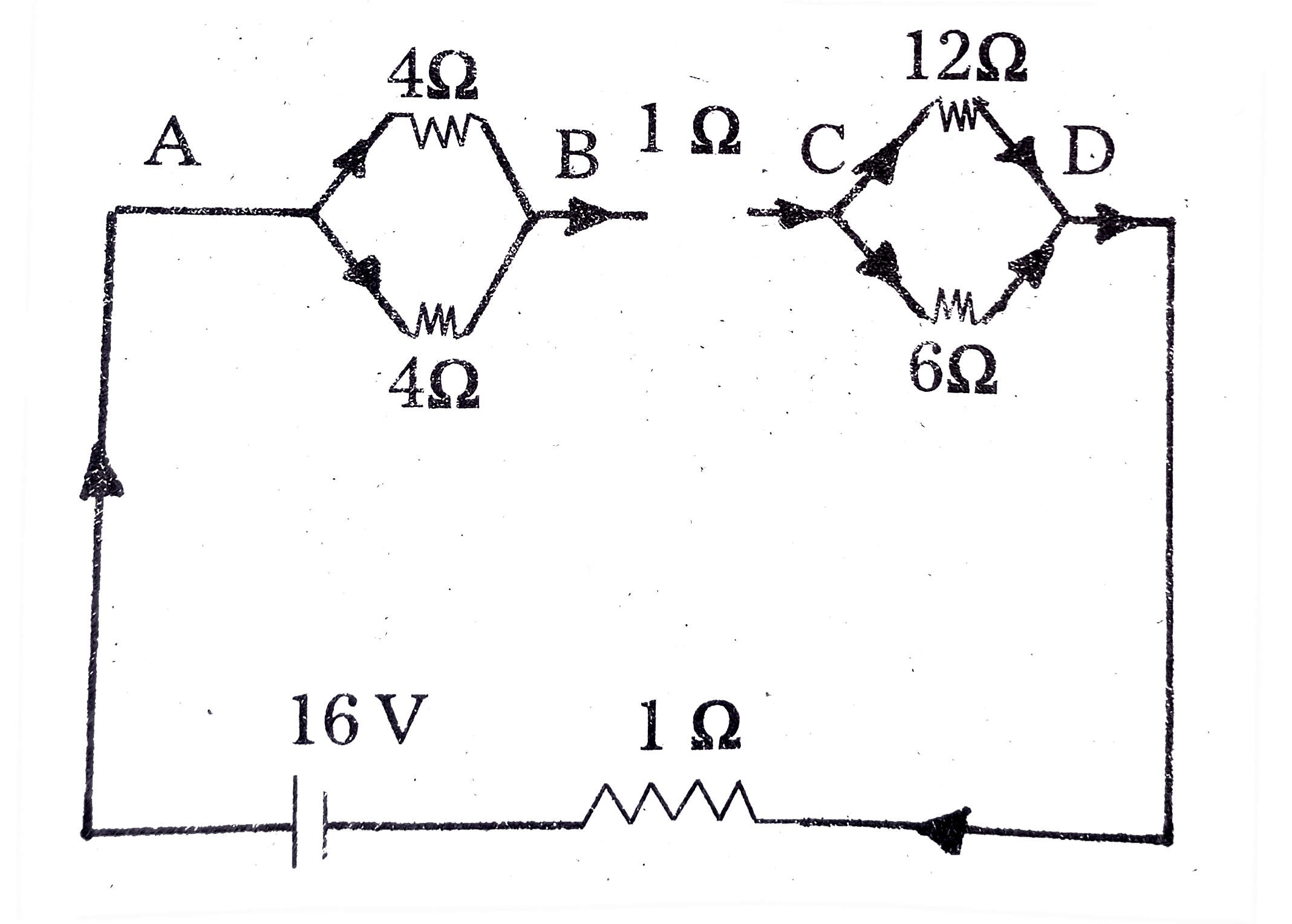
View SolutionA network of resistor is connected to a 16 V battery with internal resistance of 1 Omega , a shown in fig. (a) complete the equivalent resistance of the network.
View SolutionA network of resistor is connected to a 16 V battery with internal resistance of 1Ω, a shown in fig.
Obtain the current in each resistor.
View SolutionA network of resistor is connected to a 16 V battery with internal resistance of 1Ω, a shown in fig.
Obtain the voltage drops VAB,VBC and VCD
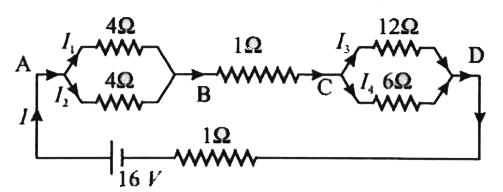
View Solutionनिम्न चित्र के अनुसार 1Ω आंतरिक प्रतिरोध के 16 V कि एक बैटरी से प्रतिरोधों के एक नेटवर्क को जोड़ा गया है ।
नेटवर्क के तुल्य प्रतिरोध कि गणना कीजिए ।
View Solutionनिम्न चित्र के अनुसार 1Ω आंतरिक प्रतिरोध के 16 V कि एक बैटरी से प्रतिरोधों के एक नेटवर्क को जोड़ा गया है ।
प्रत्येक प्रतिरोधक में धारा का मान ज्ञात कीजिए |
View Solutionचित्र में दर्शाए अनुसार 1Ω आन्तरिक प्रतिरोध की 16V की एक बैटरी से प्रतिरोधों के एक नेटवर्क को जोड़ा गया है।
वोल्टता पात VAB,VBC तथा VCD ज्ञात कीजिये।
View Solutionचित्र में दिखाए गए अनुसार आंतरिक 1Ω प्रतिरोध के की एक बैटरी में प्रतिरोधों के 16 V एक नेटवर्क को जोड़ा गया है
नेटवर्क का तुल्य प्रतिरोध परिकलित कीजिये |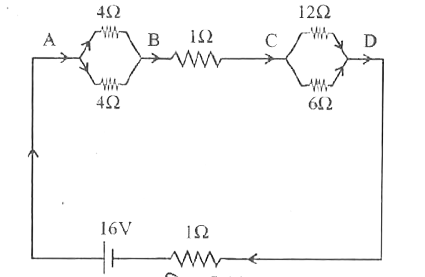
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Omega as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops V_(BC) and V_(CD)
View Solution
