A billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
2v0h5r2
5v0h2r2
5v0r25h
5v0r22h
The correct Answer is:B
To find the angular velocity ω0 acquired by the billiard ball when it is hit, we can follow these steps:
Step 1: Understand the problem
The billiard ball is hit at a height h above its center, resulting in a linear velocity v0. We need to determine the angular velocity ω0 that the ball acquires.
Step 2: Identify the forces and torques
When the ball is struck, a force F is applied at a distance h from the center of mass. This creates a torque τ about the center of mass.
Step 3: Calculate the torque
The torque τ can be calculated using the formula:
τ=F⋅h
Step 4: Relate torque to angular acceleration
The torque is also related to the moment of inertia I and angular acceleration α by the equation:
τ=I⋅α
For a solid sphere, the moment of inertia I is given by:
I=25mr2
Thus, we can write:
F⋅h=25mr2⋅α
Step 5: Relate linear and angular acceleration
The angular acceleration α can be expressed in terms of angular velocity ω0 and time t:
α=ω0t
Substituting this into the torque equation gives:
F⋅h=25mr2⋅ω0t
Step 6: Express force in terms of linear acceleration
The force F can be expressed as:
F=m⋅a
where a is the linear acceleration. Since the ball acquires a linear velocity v0 over time t, we can write:
a=v0t
Thus, substituting for F:
F=m⋅v0t
Step 7: Substitute back into the torque equation
Now substituting F back into the torque equation:
m⋅v0t⋅h=25mr2⋅ω0t
Step 8: Cancel common terms
We can cancel m and t from both sides:
v0⋅h=25r2⋅ω0
Step 9: Solve for angular velocity ω0
Rearranging the equation to solve for ω0:
ω0=5v0h2r2
Final Result
The angular velocity ω0 acquired by the billiard ball is:
ω0=5v0h2r2
---
The billiard ball is hit at a height h above its center, resulting in a linear velocity v0. We need to determine the angular velocity ω0 that the ball acquires.
When the ball is struck, a force F is applied at a distance h from the center of mass. This creates a torque τ about the center of mass.
The torque τ can be calculated using the formula:
τ=F⋅h
The torque is also related to the moment of inertia I and angular acceleration α by the equation:
τ=I⋅α
For a solid sphere, the moment of inertia I is given by:
I=25mr2
Thus, we can write:
F⋅h=25mr2⋅α
The angular acceleration α can be expressed in terms of angular velocity ω0 and time t:
α=ω0t
Substituting this into the torque equation gives:
F⋅h=25mr2⋅ω0t
The force F can be expressed as:
F=m⋅a
where a is the linear acceleration. Since the ball acquires a linear velocity v0 over time t, we can write:
a=v0t
Thus, substituting for F:
F=m⋅v0t
Now substituting F back into the torque equation:
m⋅v0t⋅h=25mr2⋅ω0t
We can cancel m and t from both sides:
v0⋅h=25r2⋅ω0
Rearranging the equation to solve for ω0:
ω0=5v0h2r2
The angular velocity ω0 acquired by the billiard ball is:
ω0=5v0h2r2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct86videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct36videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
Similar Questions
A uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position ifView Solution
A solid sphere and a hollow sphere both of same mass and same radius are hit by a cue at a height h above the centre C. In which case,
(a). Linear velocity will be more?
(b). Angular velocity will be more?
(c). rotational kinetic energy will be more?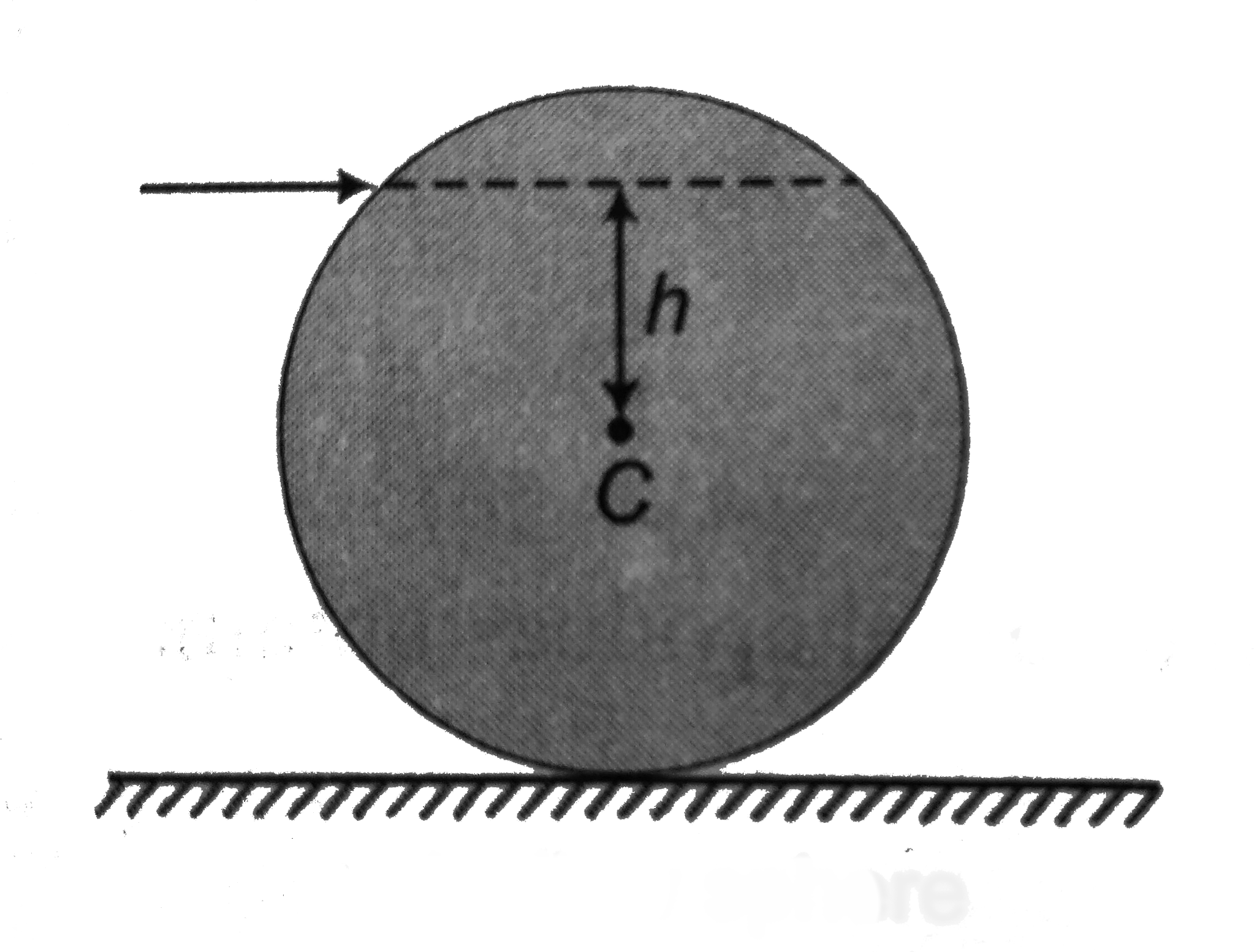 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If a projectile having horizontal range of 24 m acquires a maximum height of 8 m, then its initial velocity and the angle of projection are
A5√g,sin−1(0.6)B5√g,sin−1(0.8)C24√g,sin−1(0.6)D8√g,sin−1(0.8) - Question 2 - Select One
A spherical metal ball of mass m and radius (r) is falling through a viscous medium. The value of its terminal velocity is proportional to
A1/r onlyBm/rC(m/r)1/2Dm only

A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View SolutionA disc of radius R and mass m is projected on to a horizontal floor with a backward spin such that its centre of mass speed is v0 and angular velocity is ω0. What must be the minimum value of ω0 so that the disc eventually returns back?
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
 View Solution
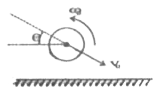
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
 View Solution
View Solution

