A uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
The correct Answer is:4
To solve the problem of finding the force on the hinge when a uniform rod of mass m is released from a horizontal position and passes through the vertical position, we can follow these steps:
1. Identify the System:
We have a uniform rod of mass m and length l hinged at its upper end. The rod is released from a horizontal position.
2. Determine the Forces Acting on the Rod:
When the rod is in the vertical position, the forces acting on it are:
- The weight of the rod acting downwards, mg.
- The normal force N exerted by the hinge acting upwards.
3. Calculate the Potential Energy Loss:
The center of mass of the rod is located at a distance of l2 from the hinge. When the rod is horizontal, the potential energy is maximum, and as it falls to the vertical position, the height of the center of mass decreases by l2.
Loss in Potential Energy=mg⋅l2
4. Use the Conservation of Energy:
The loss in potential energy converts into kinetic energy. The kinetic energy of the rod when it is vertical can be expressed in terms of its angular velocity ω:
12Iω2=mg⋅l2
where I is the moment of inertia of the rod about the hinge, which is 13ml2.
5. Substitute the Moment of Inertia:
Substitute I into the equation:
12(13ml2)ω2=mg⋅l2
Simplifying gives:
ml2ω26=mg⋅l2
6. Solve for Angular Velocity ω2:
Rearranging the equation:
ω2=3gl
7. Calculate the Centripetal Force:
The centripetal force acting on the center of mass of the rod when it is vertical is given by:
Fc=m⋅l2⋅ω2=m⋅l2⋅3gl=3mg2
8. Apply Newton’s Second Law:
According to Newton’s second law, the net force acting on the rod in the vertical direction is:
N−mg=Fc
Substituting Fc gives:
N−mg=3mg2
9. Solve for the Normal Force N:
Rearranging the equation to solve for N:
N=3mg2+mg=5mg2
Final Answer:
The force on the hinge when the rod passes through the vertical position is:
N=5mg2
We have a uniform rod of mass m and length l hinged at its upper end. The rod is released from a horizontal position.
When the rod is in the vertical position, the forces acting on it are:
- The weight of the rod acting downwards, mg.
- The normal force N exerted by the hinge acting upwards.
The center of mass of the rod is located at a distance of l2 from the hinge. When the rod is horizontal, the potential energy is maximum, and as it falls to the vertical position, the height of the center of mass decreases by l2.
Loss in Potential Energy=mg⋅l2
The loss in potential energy converts into kinetic energy. The kinetic energy of the rod when it is vertical can be expressed in terms of its angular velocity ω:
12Iω2=mg⋅l2
where I is the moment of inertia of the rod about the hinge, which is 13ml2.
Substitute I into the equation:
12(13ml2)ω2=mg⋅l2
Simplifying gives:
ml2ω26=mg⋅l2
Rearranging the equation:
ω2=3gl
The centripetal force acting on the center of mass of the rod when it is vertical is given by:
Fc=m⋅l2⋅ω2=m⋅l2⋅3gl=3mg2
According to Newton’s second law, the net force acting on the rod in the vertical direction is:
N−mg=Fc
Substituting Fc gives:
N−mg=3mg2
Rearranging the equation to solve for N:
N=3mg2+mg=5mg2
The force on the hinge when the rod passes through the vertical position is:
N=5mg2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
16 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A uniform thin rod of mass 'm' and length '3l' is released from rest from horizontal position as shown. When it passes through the vertical line AD, it gets broken at point 'C' without jerk. Find the angle (in radian) rotated by rod BC till its centre of mass passes through the horizontal line PQ frm the instant of breakage (g=10m/s2) (hinge is smooth)

View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View SolutionTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:

View SolutionA uniform bar AB of mass m and a ball of the same mass are released from rest from the same horizontal position. The bar is hinged at end A. There is gravity downwards. What is the distance of the point from point B that has the same acceleration as the ball, immediately after release?

View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
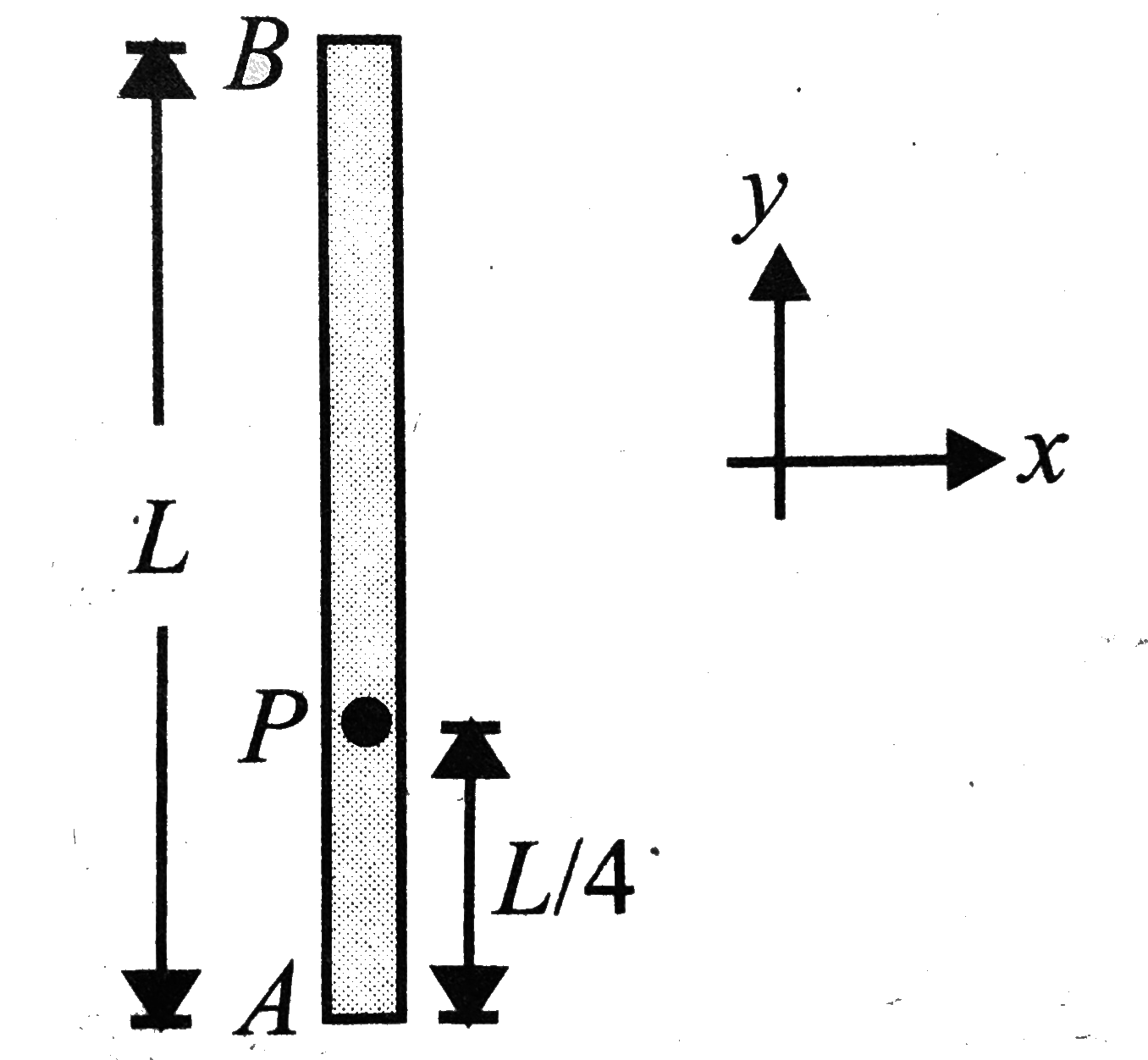
The acceleration of end B of the rod is
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod is
View SolutionA simple pendulum A and a homogeneous rod B hinged at its enda are released from horizontal position as shown in figure.

View SolutionA light rigid rod of length 4m is connected rigidly with two identical particles each of mass m=2kg. the free end of the rod is smoothly pivoted at O. The rod is released from rest from its horizontal position at t=0. Find the
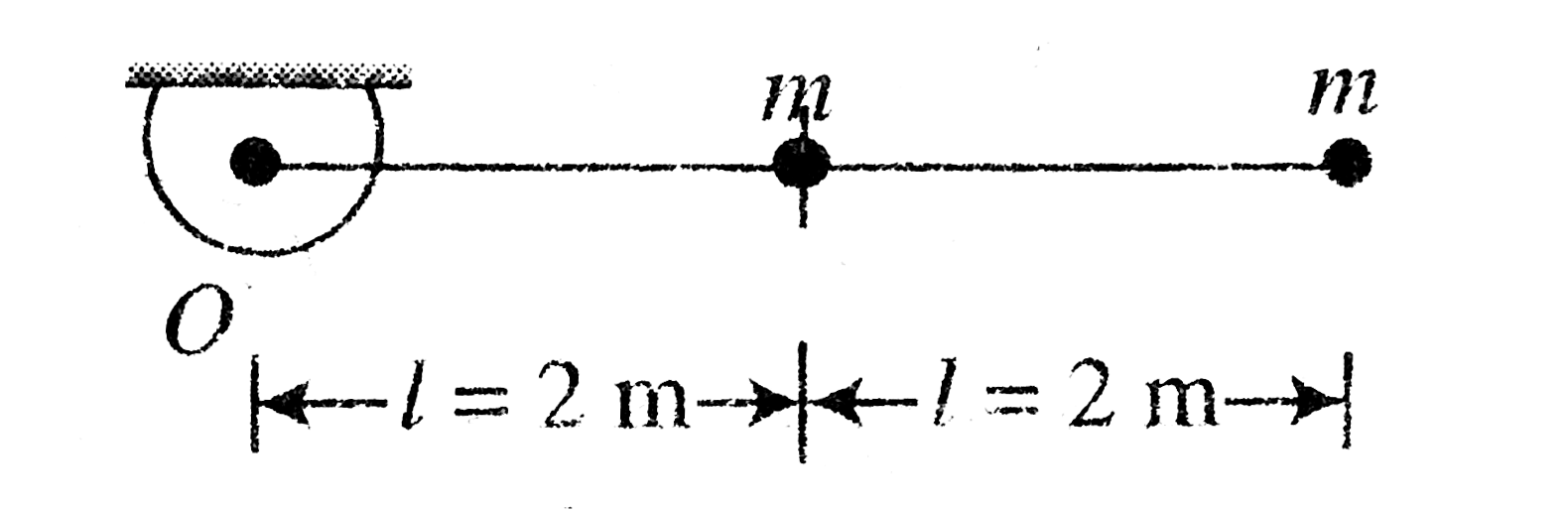
reaction offered by the pivot at t=0 (in N).
View Solution
