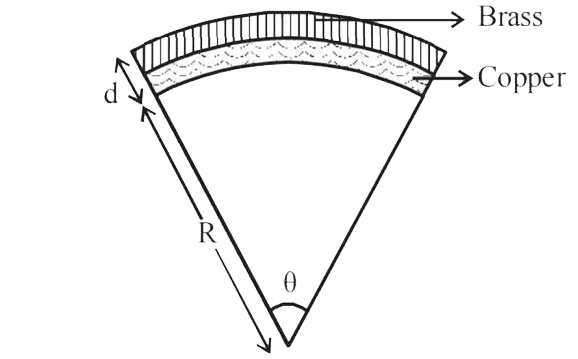
A bimetallic strip is formed out of two identical strips one of copper and the other of brass. The coefficients of linear expansion of the strip goes up by ΔTand the strip bends to from an arc of radius of curvature R. Then R is.
proportional to ΔT
inversely proportional to ΔT
proportional to |αB−αC|
inversely proportional to |αB−αC|
The correct Answer is:B, D
(b,d)
Co-efficient of linear expansion of brass is greater than that
of copper i.e., αB>αC. Now,
LB=L0(1+αBΔT)
or, (R+d)θ=L0(1+αBΔT)
Again, LC=L0(1+αCΔT)
or, Rθ=L0(1+αCΔT)
∴(R+d)θRθ=1+αBΔT1+αCΔT
or, R+dR=(1+αBΔT)(1+αCΔT),byb∈omial<br>theoram.<br>or1+d/R=1+(alpha_B-alpha_C)DeltaT-alpha_B alpha_C(DeltaT)^2<br>or,d/R=(alpha_B-alpha_C) DeltaT or R=d/((alpha_B-alpha_C)DeltaT)<br>:. Rprop1/(DeltaT) and Rprop1/|alpha_B-alpha_C|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A bimetallic strip is formed out of two identical strips one of copper and the other of brass. The co-efficients of linear expansion of the two metals are αC and αB. On heating, the the strip bends to form an are of radius of curvature R. Then R is
Aproportional to ΔTBinversely proportional to ΔTCproportional to |αB−αC|DInversely proportional to |αB−αC|A bimetallic strip is composed of two identical strips, one of steel and other of brass. When the temperature of the strip is raised by ΔT , it bends to form arc of curvature R. If the coefficients of linear expansion of steel and brass are α1 and α2 , respectively, then R is
Adirectly proportional to |α1−α2|Binversely proportional to |α1−α2|Cdirectly proportional to ΔTDNONE OF THESEIn figure which strip brass or steel have higher coefficient of linear expansion.
 Abrass stripBsteel stripCboth strips has same coefficient of linear expansionDcannot be decided from given data
Abrass stripBsteel stripCboth strips has same coefficient of linear expansionDcannot be decided from given data
Two straight metallic strips each of thickness t and length l are rivetted together. Their coefficients of linear expansions areα1andα2. If they are heated through temperature ΔT, the bimetallic strip will bend to form an arc of radius
View SolutionA bimetalis strip conists of two metakl strips with diffesrent coefficients of linear expansion α1 and α2 each of small thickness d and length L0 at T0. They are bonded together and, with a change in temperature De<AT, will curve in a circular arc, as shown in figure. Show that the radius of curvature R is given approximately be
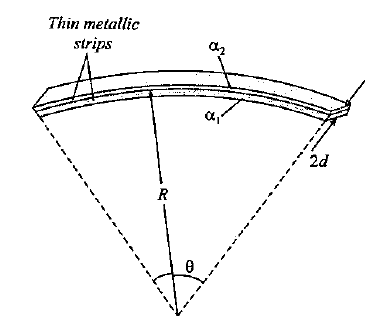
R=d(α2−α1)ΔT
View SolutionA bimetallic is made of two strips A and B having coefficients of linear expansion α4andαB. If αA<αB, then on heating, the strip will
View SolutionA bimetallic is made of two strips A and B having coefficients of linear expansion α4andαB. If αA<αB, then on heating, the strip will
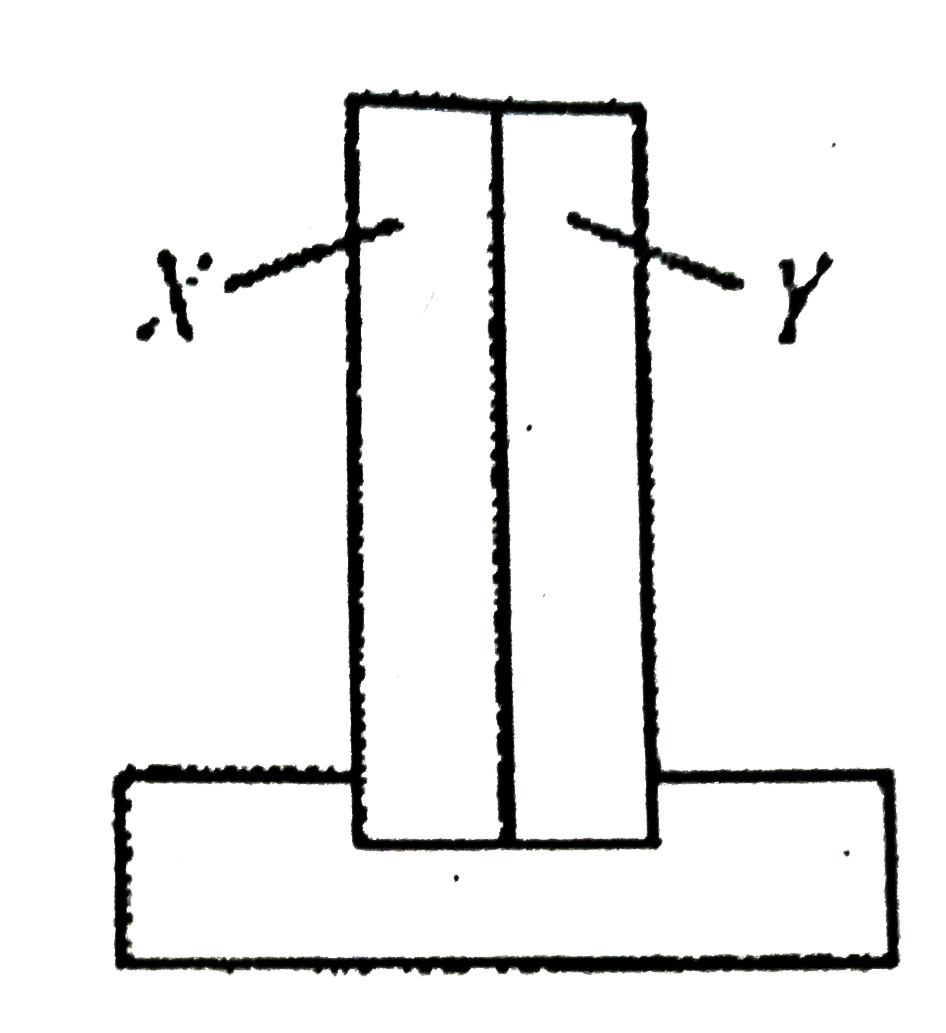
View SolutionA bimetallic strip consists of metals X and Y. It mounted rigidly at the base as shown. The metal X has a higher coefficient of expansion compared to that for metal Y. When the bimetallic strip is placed in a cold bath
View Solution

