A block is moving on an inclined plane making an angle $45^{\circ}$ with the horizontal and the coefficient of friction is $μ$ . The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define $N = 10 μ$ , then N is

Video Solution

Text Solution

Verified by Experts

The correct Answer is:5

Case 1 For pushing the block up

$F_{1} = m g {sin 45}^{\circ} + μ m g {cos 45}^{\circ}$
$F_{1} = \frac{m g}{\sqrt{2}} + \frac{μ m g}{\sqrt{2}}$

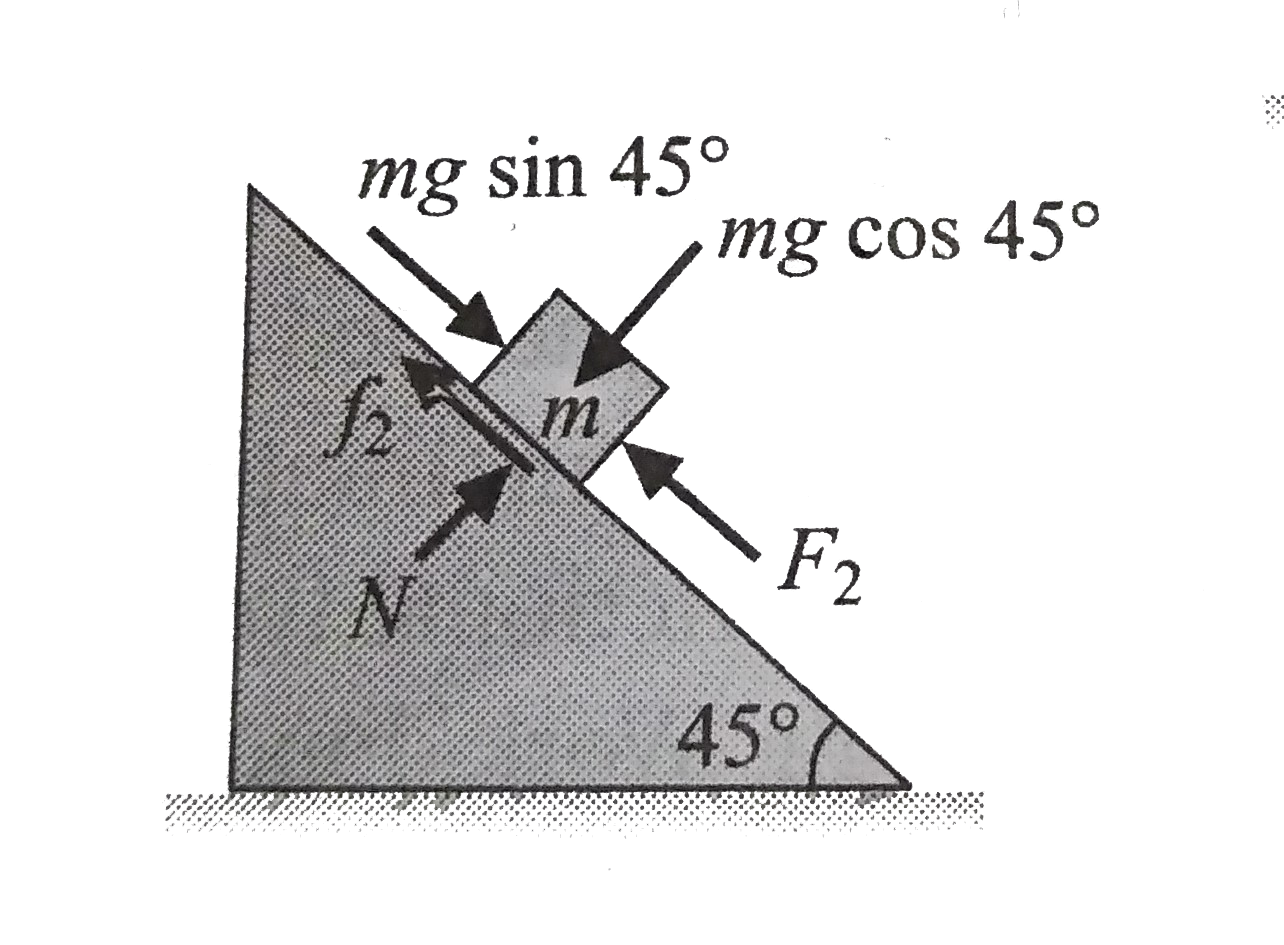
Case II force required to justpervent the block froin sliding down
$F_{1} = m g {sin 45}^{\circ} - μ m g {cos 45}^{\circ}$
$F_{2} = \frac{m g}{\sqrt{2}} - \frac{μ m g}{\sqrt{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A brick of mass 2kg just begins to slide down on inclined plane at an angle of $45^{\circ}$ with the horizontal. The force of friction will be
A $19.6 {sin 45}^{\circ}$
B $19.6 {cos 45}^{\circ}$
C $9.8 {sin 45}^{\circ}$
D $9.8 {cos 45}^{\circ}$
Question 2 - Select One
A brick of mass 2kg begins to slide down on a plane inclined at an angle of $45^{\circ}$ with the horizontal. The force of friction will be
A $19.6 {sin 45}^{\circ}$
B $19.6 {cos 45}^{\circ}$
C $9.8 {sin 45}^{\circ}$
D $9.8 {cos 45}^{\circ}$
Question 3 - Select One
A block of mass m slides down an inclined plane which makes an angle $θ$ with the horizontal. The coefficient of friction between the block and the plane is $μ$ . The force exerted by the block on the plane is
A $m g cos θ$
B $\sqrt{μ^{2} + 1} m g cos θ$
C $\frac{μ m g cos θ}{\sqrt{μ^{2} + 1}}$
D $μ m g θ$

CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 2-Integer type

A block is moving on an inclined plane making an angle 45^@ with the h...
07:31

Home
Ask Doubt
Profile