A block of known mass is suspended from a fixed support through a ligh spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
To find the time period of vertical oscillation of a block suspended from a spring, we can follow these steps:
Step 1: Understand the forces acting on the block
When the block is in equilibrium, two main forces are acting on it:
- The gravitational force (weight) acting downwards, which is given by Fg=mg, where m is the mass of the block and g is the acceleration due to gravity.
- The spring force acting upwards, which is given by Hooke's law as Fs=kx0, where k is the spring constant and x0 is the extension of the spring.
Step 2: Set up the equilibrium condition
At equilibrium, the forces balance each other:
mg=kx0
This equation relates the weight of the block to the spring force.
Step 3: Solve for the spring constant k
From the equilibrium condition, we can express the spring constant k in terms of known quantities:
k=mgx0
Step 4: Use the formula for the time period of vertical oscillation
The time period T of a mass-spring system in simple harmonic motion is given by the formula:
T=2π√mk
Now, substitute the expression for k from Step 3 into this formula.
Step 5: Substitute k into the time period formula
Substituting k=mgx0 into the time period formula gives:
T=2π√mmgx0=2π√mx0mg
Step 6: Simplify the expression
This simplifies to:
T=2π√x0g
This final expression shows that the time period of vertical oscillation depends only on the extension x0 of the spring and the acceleration due to gravity g.
Conclusion
Yes, we can find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium, and it is given by:
T=2π√x0g
---
When the block is in equilibrium, two main forces are acting on it:
- The gravitational force (weight) acting downwards, which is given by Fg=mg, where m is the mass of the block and g is the acceleration due to gravity.
- The spring force acting upwards, which is given by Hooke's law as Fs=kx0, where k is the spring constant and x0 is the extension of the spring.
At equilibrium, the forces balance each other:
mg=kx0
This equation relates the weight of the block to the spring force.
From the equilibrium condition, we can express the spring constant k in terms of known quantities:
k=mgx0
The time period T of a mass-spring system in simple harmonic motion is given by the formula:
T=2π√mk
Now, substitute the expression for k from Step 3 into this formula.
Substituting k=mgx0 into the time period formula gives:
T=2π√mmgx0=2π√mx0mg
This simplifies to:
T=2π√x0g
This final expression shows that the time period of vertical oscillation depends only on the extension x0 of the spring and the acceleration due to gravity g.
Yes, we can find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium, and it is given by:
T=2π√x0g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Knowledge Check
When a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
AT=T1+T2B1T=1T1+1T2CT2=T21+T22D1T2=1T21+1T2
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionFind the period of a vertical spring - block system by both methods.
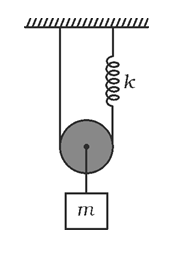
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
View SolutionA spring mass system has time period of 2 second. What should be the spring constant of spring if the mass of the block is 10grams ?
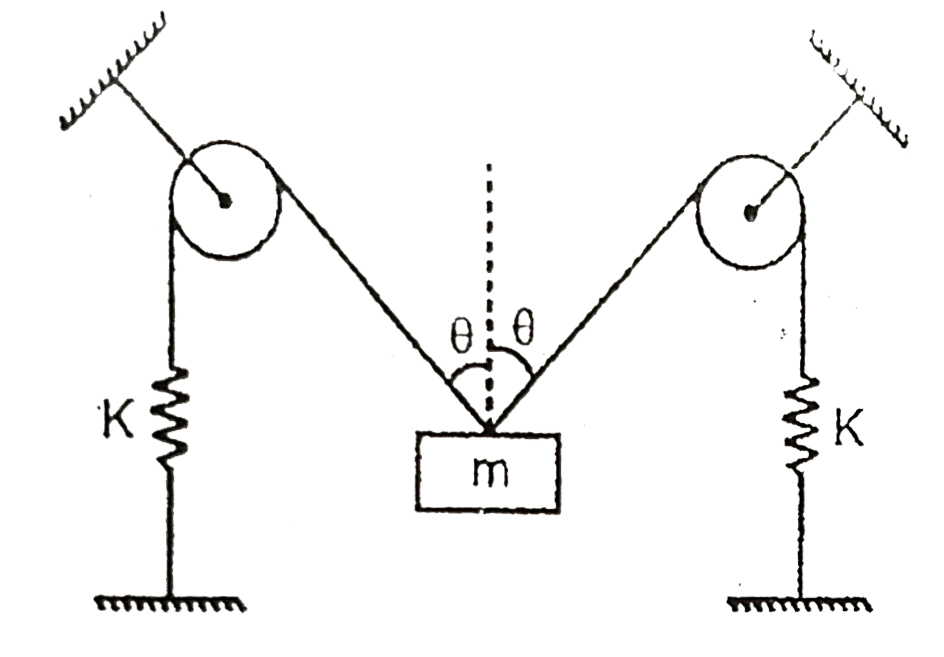
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View Solution