A block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
The correct Answer is:3.162rad s−10.0141m
To solve the problem step by step, we need to find the angular frequency and amplitude of oscillation for a block attached to a spring.
Given Data:
- Mass of the block, m=0.01kg
- Spring constant, k=10−1N/m
- Energy of oscillation, E=10−5J
Step 1: Calculate Angular Frequency
The formula for angular frequency ω in simple harmonic motion (SHM) is given by:
ω=√km
Substituting the values of k and m:
ω=√10−10.01=√10−110−2=√101=√10
Thus, the angular frequency ω is:
ω=√10rad/s
Step 2: Calculate Amplitude
The total energy in SHM is given by the formula:
E=12kA2
Where A is the amplitude. Rearranging the formula to solve for A:
A2=2Ek
Substituting the values of E and k:
A2=2×10−510−1=2×10−50.1=2×10−4
Now, taking the square root to find A:
A=√2×10−4=√2×10−2
Calculating √2:
A≈1.414×10−2m
Final Results:
- Angular frequency ω=√10rad/s
- Amplitude A≈1.414×10−2m
- Mass of the block, m=0.01kg
- Spring constant, k=10−1N/m
- Energy of oscillation, E=10−5J
The formula for angular frequency ω in simple harmonic motion (SHM) is given by:
The total energy in SHM is given by the formula:
- Angular frequency ω=√10rad/s
- Amplitude A≈1.414×10−2m
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (PERIOD OF OSCILLATION OF (i) A LIQUID IN A U-TUBE, (ii) TEST TUBE FLOAT, (iii) (iii) A PISTON IN AN ENGINE etc.)
9 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM ENERGY OF AS.H. OSCILLATOR )
9 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
A block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass m1=1kg is attached to a spring of force constant k=24N/cm at one end and attached to a string tensioned by mass m2=5kg . Dedcue the frequency of oscillaitons of the system. If m2 is initially supported in hand and then suddenly released, find

(a) instantaneous tension just after m2 is released . ltbr> (b) the maximum displacement of m1.
(c) the maximum and minimum tensions in the string during oscillations.
View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is putted rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View SolutionA particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
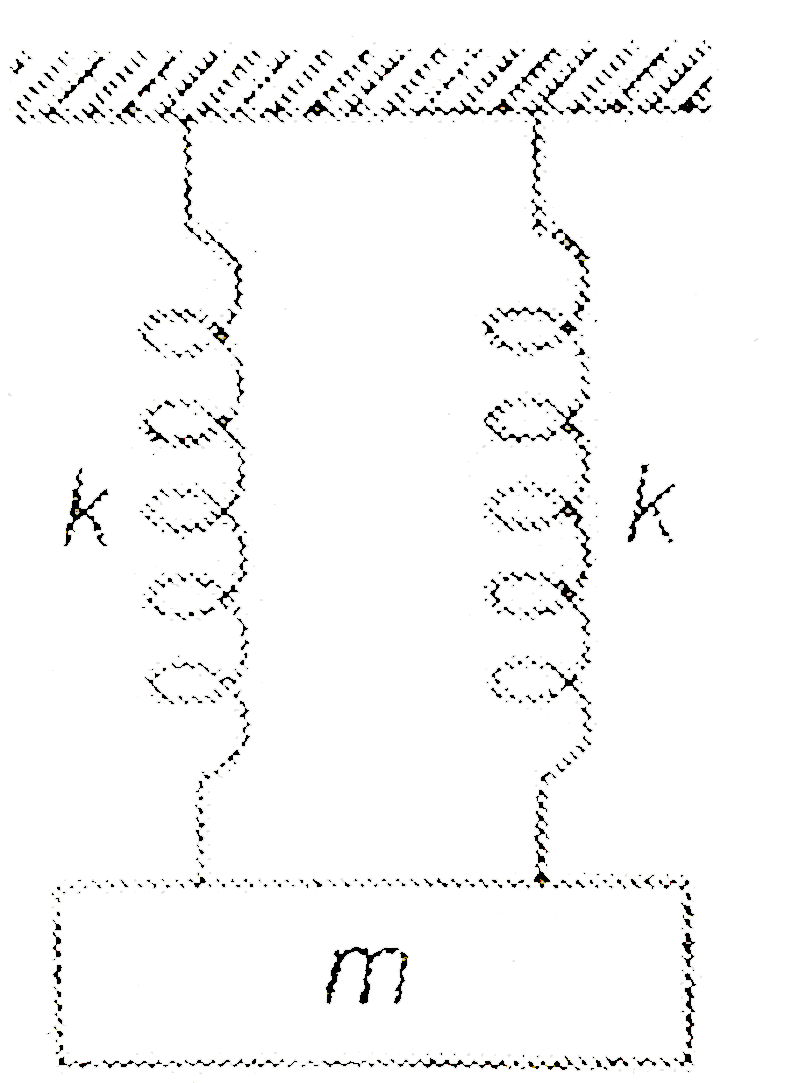
If instead of breaking one spring m/2 mass would have fallen from the block, then what will be the new amplitude?
View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
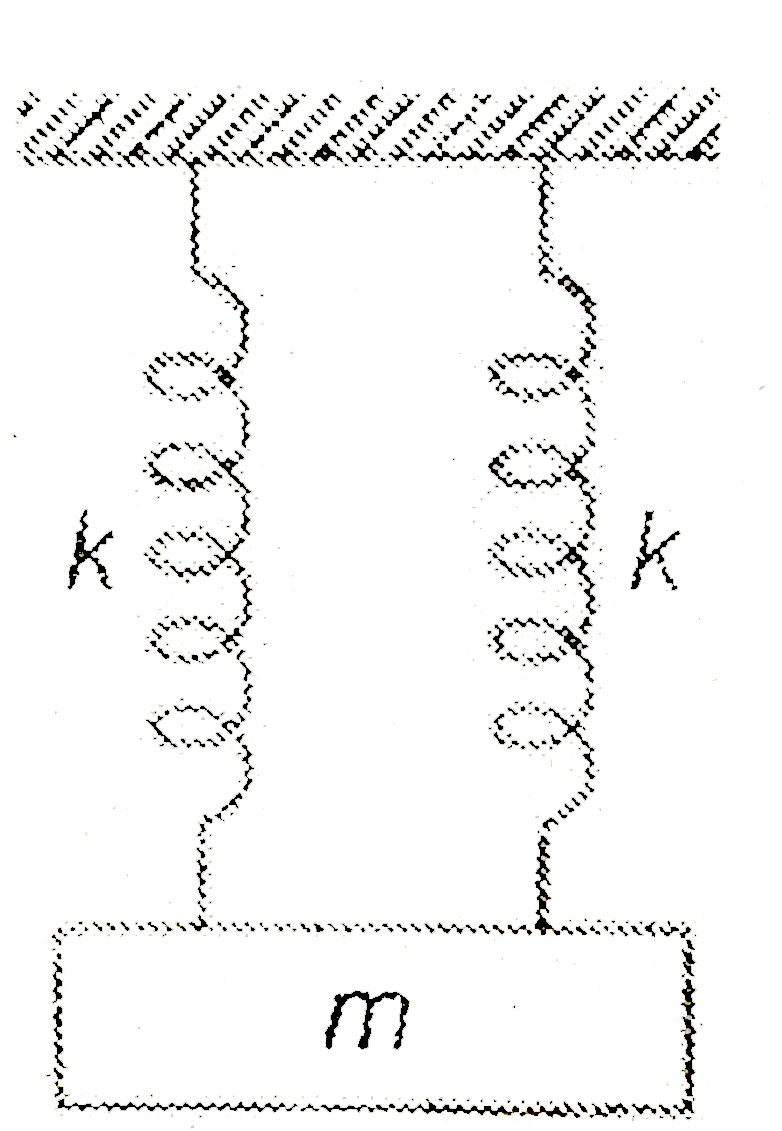
What is the new amplitude of osciallation of the block.
View SolutionIf two springs of force constants 7Nm−1and9Nm−1 are connected in series and is fixed to a body of mass 100 g. Find the period of oscillation.
View Solution
