A block of mass 10 kg is sliding on a surface inclined at 30∘ with horizontal . If coefficient of friction between the block and the surface is 0.5 , find acceleration produced in the block . Take g=9.8m/2 .
To find the acceleration produced in the block sliding down an inclined plane, we can follow these steps:
Step 1: Identify the forces acting on the block
- The gravitational force acting downward: Fg=mg
- The component of gravitational force acting parallel to the incline: F∥=mgsin(θ)
- The component of gravitational force acting perpendicular to the incline: F_{\perpendicular} = mg \cos(\theta)
- The normal force N acting perpendicular to the incline
- The frictional force Ff acting opposite to the direction of motion: Ff=μN
Step 2: Calculate the gravitational force components
Given:
- Mass of the block, m=10kg
- Angle of incline, θ=30∘
- Coefficient of friction, μ=0.5
- Acceleration due to gravity, g=9.8m/s2
Calculate F∥ and F_{\perpendicular} :
F∥=mgsin(θ)=10×9.8×sin(30∘)=10×9.8×0.5=49N
F_{\perpendicular} = mg \cos(\theta) = 10 \times 9.8 \times \cos(30^\circ) = 10 \times 9.8 \times \frac{\sqrt{3}}{2} \approx 84.87 \, \text{N}
Step 3: Calculate the normal force
Since there is no vertical motion, the normal force N is equal to the perpendicular component of the gravitational force:
N = F_{\perpendicular} = 84.87 \, \text{N}
Step 4: Calculate the frictional force
Using the coefficient of friction:
Ff=μN=0.5×84.87≈42.44N
Step 5: Apply Newton's second law
The net force acting on the block along the incline is given by:
Fnet=F∥−Ff
Substituting the values:
Fnet=49−42.44≈6.56N
Step 6: Calculate the acceleration
Using Newton's second law F=ma:
a=Fnetm=6.5610≈0.656m/s2
Final Answer
The acceleration produced in the block is approximately 0.656m/s2.
---
- The gravitational force acting downward: Fg=mg
- The component of gravitational force acting parallel to the incline: F∥=mgsin(θ)
- The component of gravitational force acting perpendicular to the incline: F_{\perpendicular} = mg \cos(\theta)
- The normal force N acting perpendicular to the incline
- The frictional force Ff acting opposite to the direction of motion: Ff=μN
Given:
- Mass of the block, m=10kg
- Angle of incline, θ=30∘
- Coefficient of friction, μ=0.5
- Acceleration due to gravity, g=9.8m/s2
F∥=mgsin(θ)=10×9.8×sin(30∘)=10×9.8×0.5=49N
F_{\perpendicular} = mg \cos(\theta) = 10 \times 9.8 \times \cos(30^\circ) = 10 \times 9.8 \times \frac{\sqrt{3}}{2} \approx 84.87 \, \text{N}
Since there is no vertical motion, the normal force N is equal to the perpendicular component of the gravitational force:
N = F_{\perpendicular} = 84.87 \, \text{N}
Using the coefficient of friction:
Ff=μN=0.5×84.87≈42.44N
The net force acting on the block along the incline is given by:
Fnet=F∥−Ff
Substituting the values:
Fnet=49−42.44≈6.56N
Using Newton's second law F=ma:
a=Fnetm=6.5610≈0.656m/s2
The acceleration produced in the block is approximately 0.656m/s2.
Similar Questions
A block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View Solution
Knowledge Check
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8NA block of mass "5kg" is placed on a wedge having inclination of 37∘ with the horizontal. Coefficient of friction between block and wedge is 0.8. Then select the correct statement.
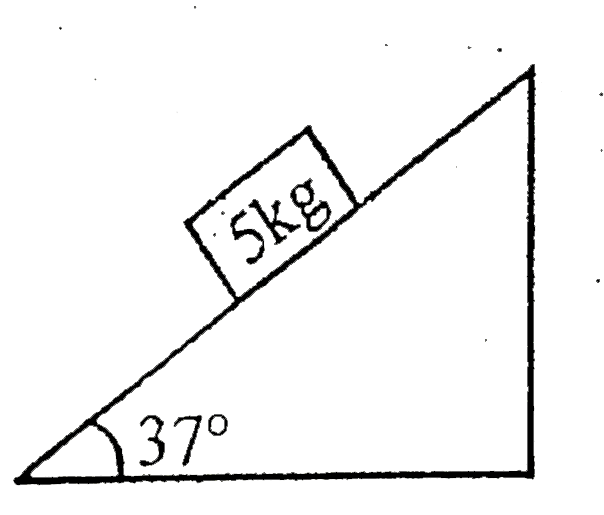 AFriction force between block and the wedge is 32 N.BFriction force between block and the wedge is 30N.CContact force between block and wedge is 80N.DContact force between bock and wedge is 40N.
AFriction force between block and the wedge is 32 N.BFriction force between block and the wedge is 30N.CContact force between block and wedge is 80N.DContact force between bock and wedge is 40N.A block of 5 kg is resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.2. What is the acceleration with which the block will remove if a force of 9.8 N is applied to it ?
A2m/s2B3m/s2C1.5m/s2D2.5m/s2
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
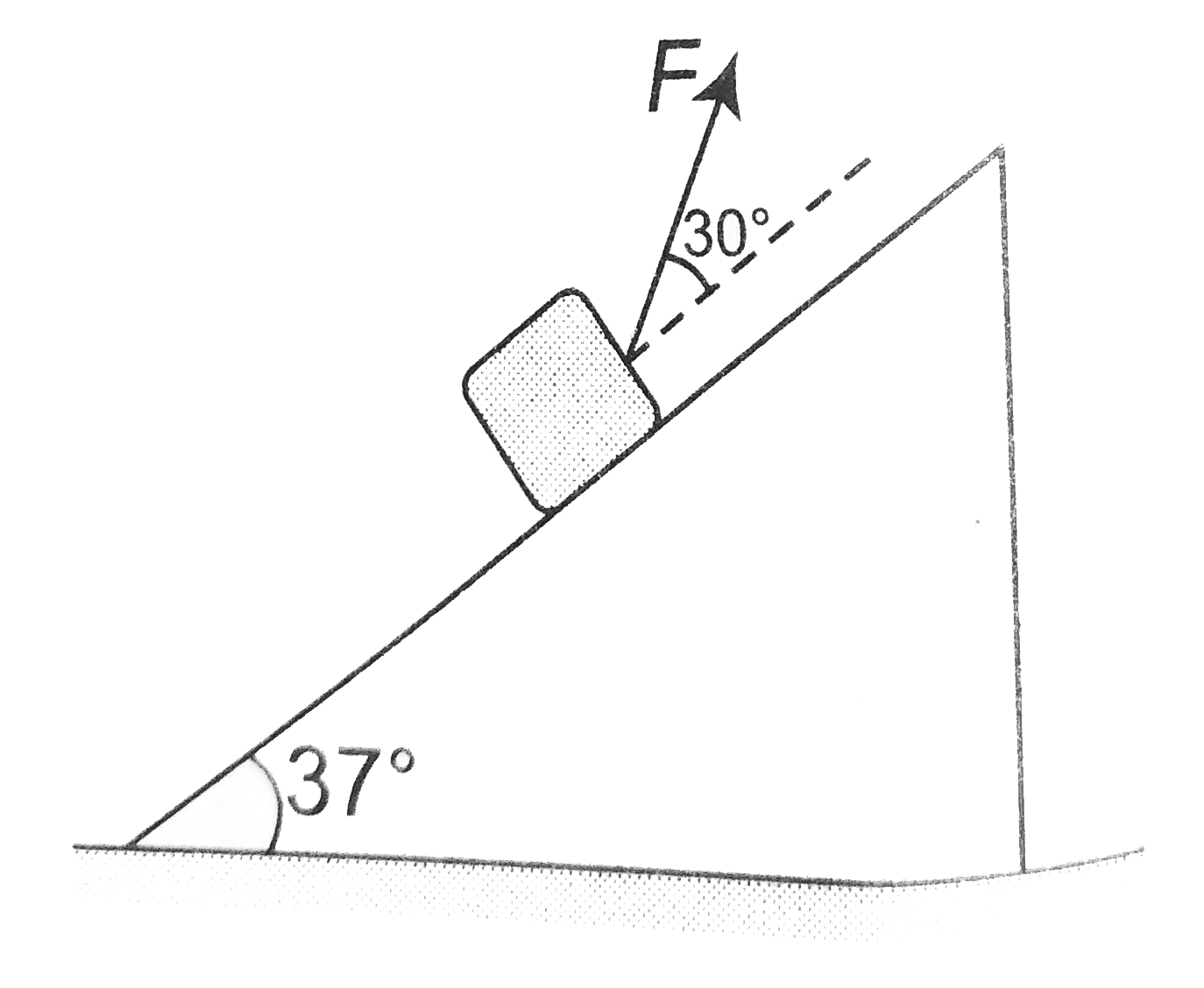
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
View SolutionA block is lying on an inclined plane which makes 60∘ with the horizontal. If coefficient of friction between block and plane is 0.25 and g=10m/s2, , then acceleration of the block when it moves along the plane will be
View SolutionA block rests on a rought inclined plane making an angle of 30∘ with horizontal. The coefficient of static friction between the block and inclined plane is 0.8 . If the frictional foerce on the block is 10N, the mass of the block in kg is (g=10m/s2)
View Solution
