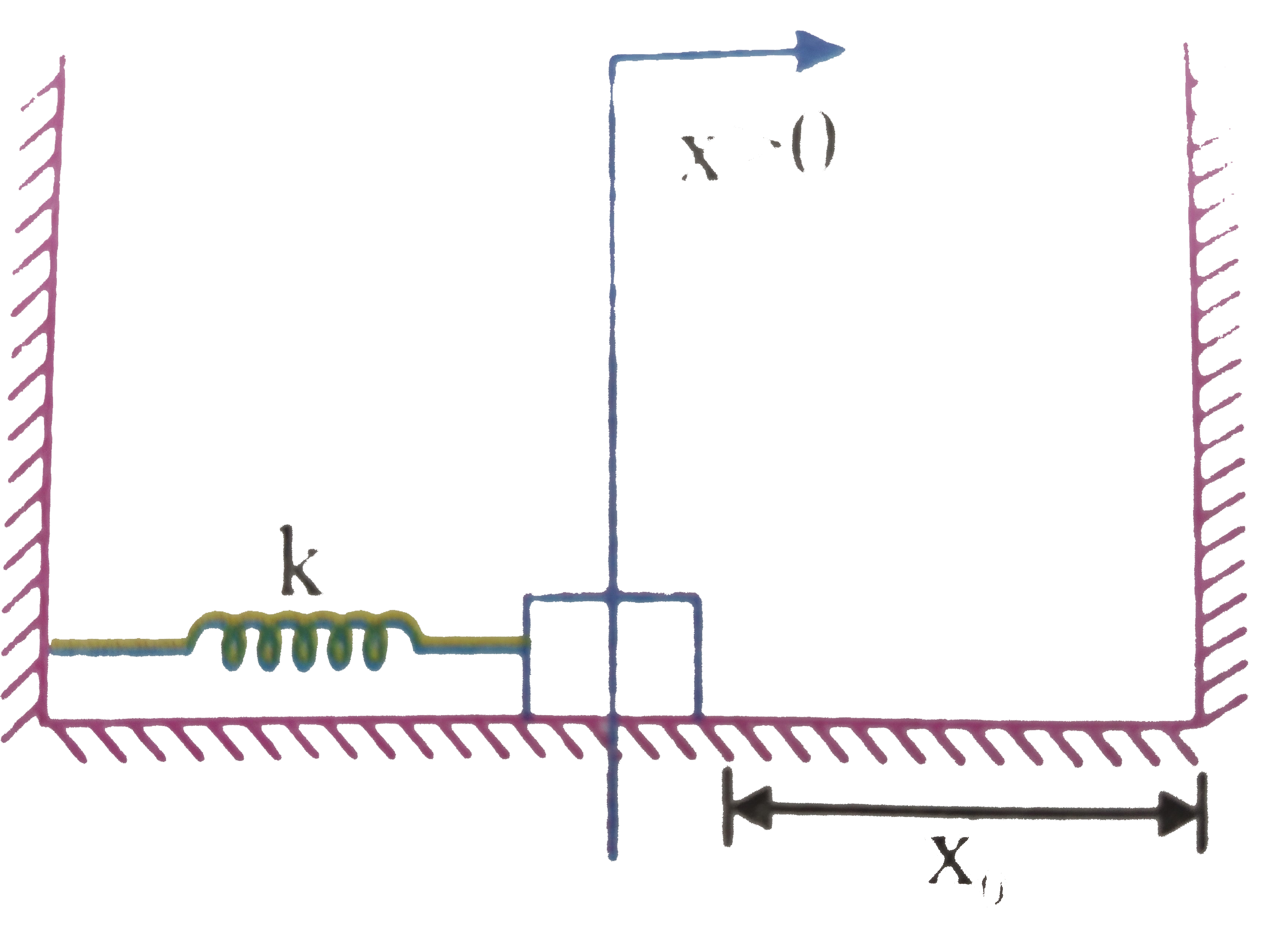
A block of mass 100g attached to a spring of stiffness 100Nmis lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

0.2 s
0.1 s
0.15 s
0.132 s
The correct Answer is:D
(d) T=2π√mk=2π√0.1100=0.198s
From x=Asinωt or 5=10sinωt
ωt=π6 or 2πTt=π6 or 2t=T6
The desired time in the question will be T2+2t
or T2+T6=2T3=(23)(0.198)=0.132s
Similar Questions
A block of mass 100g attached to a spring ofstiffness 100N/Mis lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collation with the wall is elastic then find the time period of oscillations.

View SolutionA block of mass 0.9kg attached to a spring of force constant k is lying on a frictionless floor. The spring is compressed to √2cm and the block is at a distance 1/√2cm from the wall as shown in the figure. When the block is released, it makes elastic collision with the wall and its period of motion is 0.2sec. Find the approximate value of k

View Solution
Knowledge Check
A block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
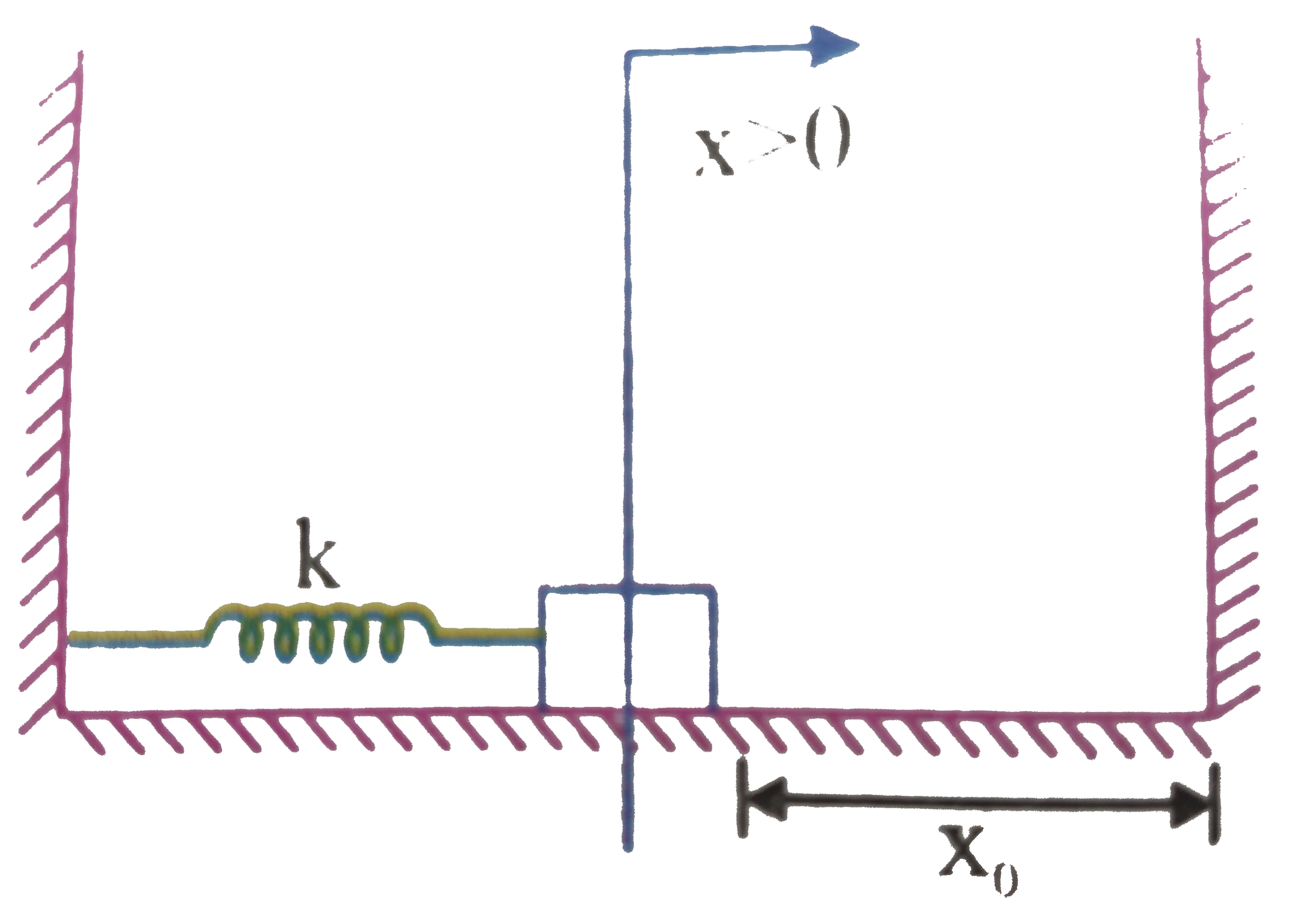
Find the time period of motion of the block:A2π3√mkB4π3√mkC3π2√mkDπ2√mkIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mkA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
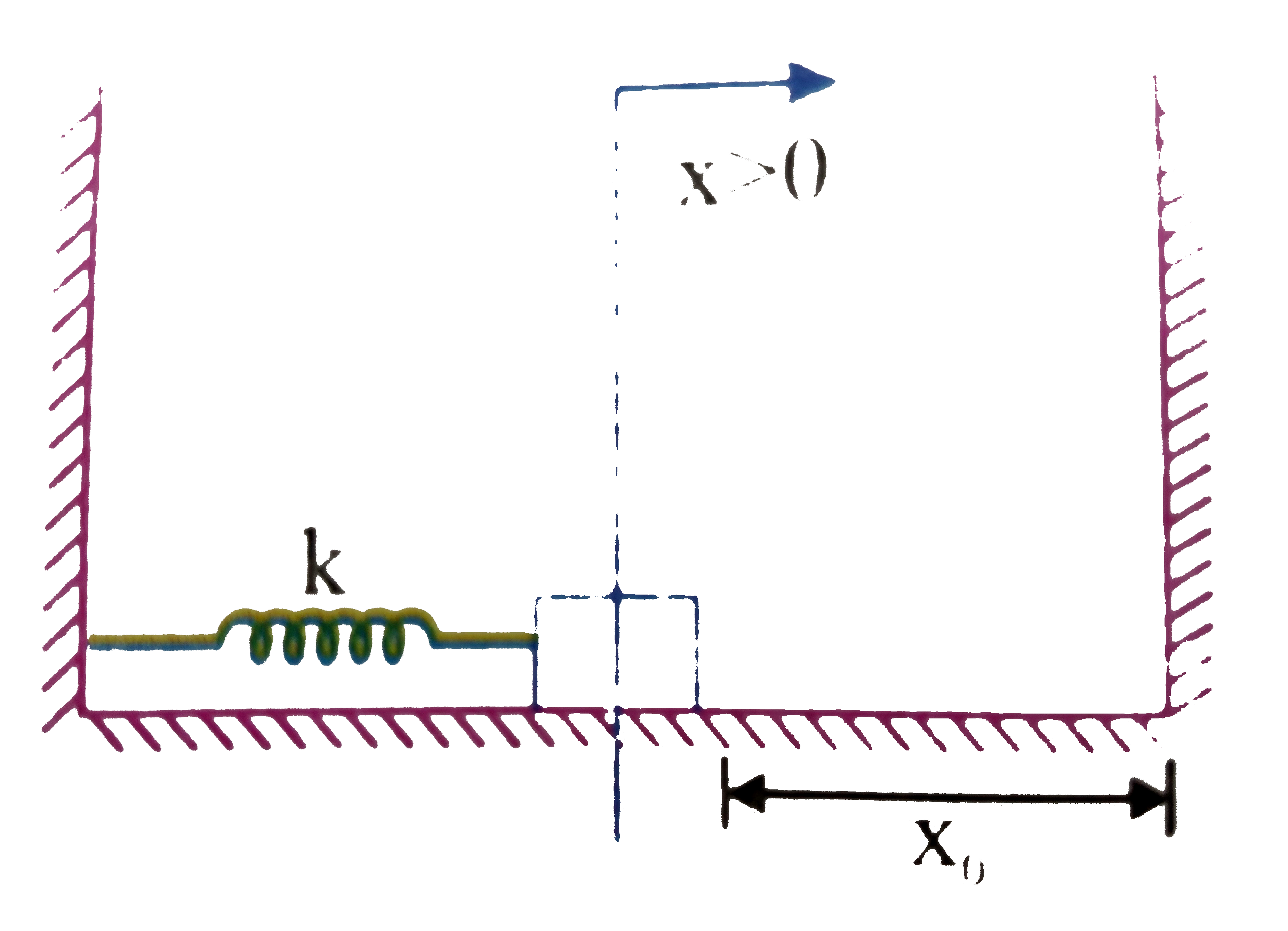
Write its equation of motion indicating position as a function of time:Ax=−2x0cosωt0<t<T2Bx=−2x0cos(ωt+2π3)T2<t<TCx=−x0cosωt0<t<T2Dx=−2x0cos(ωt+π3)T2<t<T
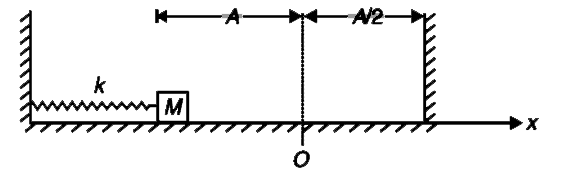
A block of mass M connected to an ideal spring of force constant k, is placed on a smooth surface. The block is pushed to the left so as to compress the spring by a length A and then it is released. The block hits an elastic wall at a distance 3A2 from its point of release. Assume the collision to be instantaneous.
(a) Calculate the time required by the block to complete one oscillation
(b) Draw the velocity - time graph for one oscillation of the block.
(c) Find the value of k for which average force experienced by the wall due to repeated hitting of the block is F0.
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
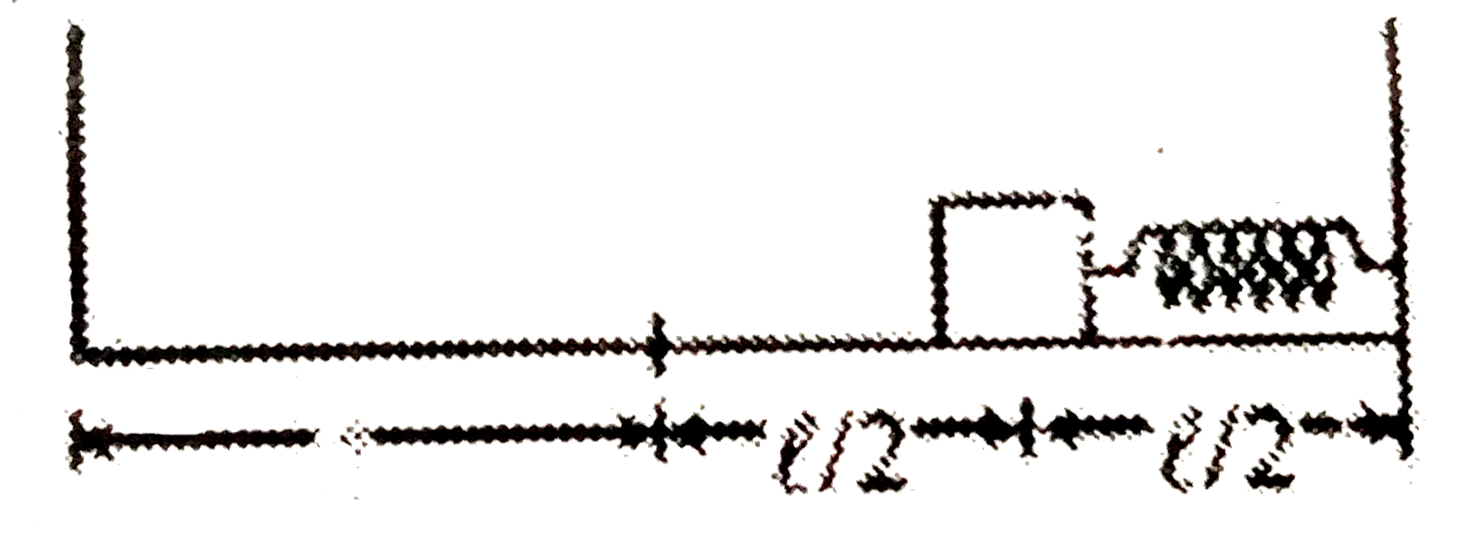
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View SolutionA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression 2x0 an block is released from rest. Collision with the wall PQ are elastic.
Draw x−t (position-time) graph for one period. Treating position of block in unstretched position of spring as origin
View Solution
