A block of mass 2 kg is pushed against a rough vertical wall with a force os 40 N. Coefficient of static friction being 05. Another horizontal force is 15 N, is applied on the block in a direction paralle to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
To solve the problem, we will analyze the forces acting on the block and determine if it will move or not.
1. Identify the Forces Acting on the Block:
- The block has a mass m=2kg.
- The gravitational force acting on the block (weight) is given by:
W=mg=2kg×10m/s2=20N(downward)
- A force of 40N is applied against the wall (perpendicular to the wall).
- A horizontal force of 15N is applied parallel to the wall.
2. Calculate the Normal Force:
- The normal force N exerted by the wall on the block is equal to the force pushing the block against the wall:
N=40N
3. Determine the Maximum Static Friction:
- The maximum static friction fmax can be calculated using the coefficient of static friction μ=0.5:
fmax=μN=0.5×40N=20N
4. Analyze the Forces in the Horizontal Direction:
- The horizontal force acting on the block is 15N (to the left).
- The maximum static friction force opposing this motion is 20N (to the right).
- Since the applied force 15N is less than the maximum static friction 20N, the block will not move.
5. Determine the Actual Frictional Force:
- Since the block does not move, the frictional force f will equal the applied horizontal force to prevent motion:
f=15N(to the right)
Conclusion:
The block will not move. The frictional force exerted by the wall on the block is 15N in the direction opposite to the applied horizontal force.
---
- The block has a mass m=2kg.
- The gravitational force acting on the block (weight) is given by:
W=mg=2kg×10m/s2=20N(downward)
- A force of 40N is applied against the wall (perpendicular to the wall).
- A horizontal force of 15N is applied parallel to the wall.
- The normal force N exerted by the wall on the block is equal to the force pushing the block against the wall:
N=40N
- The maximum static friction fmax can be calculated using the coefficient of static friction μ=0.5:
fmax=μN=0.5×40N=20N
- The horizontal force acting on the block is 15N (to the left).
- The maximum static friction force opposing this motion is 20N (to the right).
- Since the applied force 15N is less than the maximum static friction 20N, the block will not move.
- Since the block does not move, the frictional force f will equal the applied horizontal force to prevent motion:
f=15N(to the right)
The block will not move. The frictional force exerted by the wall on the block is 15N in the direction opposite to the applied horizontal force.
Topper's Solved these Questions
Similar Questions
A block of mass 4kg is pushed against a rough vertical wall with a force 80N is applied on the block in a direction parallel to the wall . Will the block move? If yes , what is acceleration of the block ?
View SolutionA block of mass 1 kg is pushed against a rough vertical wall of μ=0.1
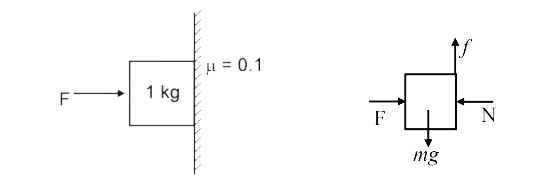
For F = 150, 50 or 100 N the force of friction on the blocks is respectively :
View Solution
Knowledge Check
A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When
 AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.
AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.A block of mass 20 kg is pushed with a horizontal force of 90N. If the coefficient of static and kinetic friction are 0.4 and 0.3, the frictional force acting on the block is (g=10ms−2)
A90NB80NC60ND30NA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 A10 NB10011NC1008ND20 N
A10 NB10011NC1008ND20 N
A block of mass 2 kg is pressed against a rigid vertical wall by a horizontal force of 100 N. If co-efficient of static and kinetic friction are each equal to 0.3 then find the magnitude and direction of frictional force on the block.

View SolutionA block of mass 20kg is pushed with a horizontal force of 90N. It the coefficient of static and kinetic friction are 0.4 and 0.3, the frictional force acting on the block is (g=10ms−2) .
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :

View Solution