A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
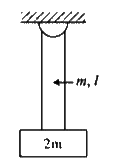
The time taken by the pulse to reach the other end of the rope is:
2√lg(√3−1)
2√lg(√3−2)
2√lg
2√lg(√3−√2)
The correct Answer is:D
Let vx be speed of pulses x distance from bottom of rope
Then vx=√(2m+maxl)gm/l=√(2l+x)g
Then time taken to go from bottom to top will be
T = L∫0dx√(2l+x)g=2√lg(√3−√2).
Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Advance MCQs with One or More Options Correct
30 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Unsolved Numerical Problems for Preparation of NSE, INPhO & IPhO
135 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Conceptual MCQs Single Option Correct
24 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
A uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
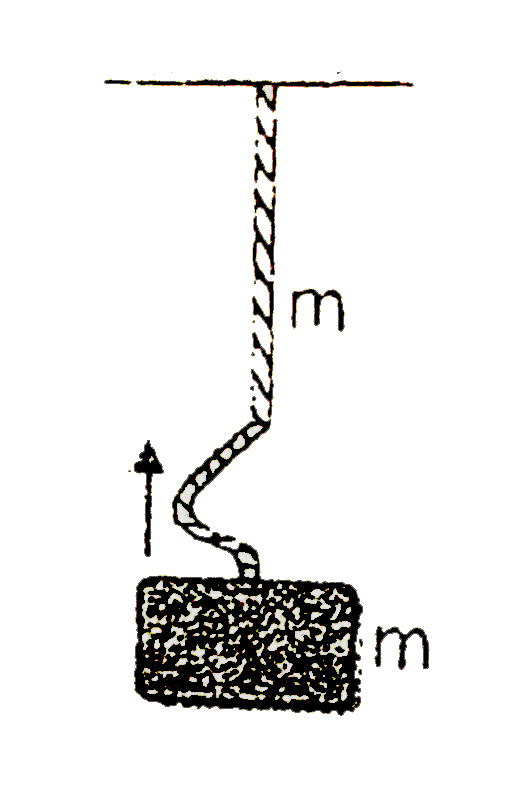
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
View Solution
Knowledge Check
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
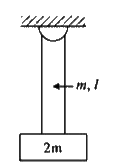
The wavelength of the pulse when it reaches the other end of the rope is :A√3λ0B√32λ0Cλ0Dλ02A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
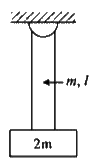
The speed of the pulseat the mid point of rope is:A√52glB√33glC√25glD√gl2A uniform rope of length L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
A√m1m2B√m1+m2m2C√m2m1D√m1+m2m1
A uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View SolutionA uniform rope of length 10 m and mass 15 kg hangs vertically from a rigid support. A block of mass 5 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.08 m is produced at the lower end of the 3 rope. The wavelength of the pulse when it reaches the top of the rope will be-
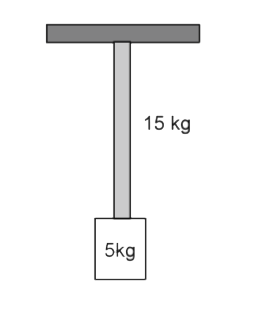
View SolutionA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View SolutionA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View SolutionA uniform rope of length 10 m and mass 3 kg hangs vertically from a rigid support. A block of mass 1 kg is attached to the free end of the rople. A transverse pulse of wavelength 0.05 m is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is
View Solution
