A block of mass 4 kg hangs from a spring constant k=400Nm. The block is pulled down through 15 cm below and released. What is its kinetic energy when the block is 10 above the equilibrium position.?
5J
2.5J
1J
1.9J
The correct Answer is:B
To solve the problem step by step, we will follow the principles of energy conservation in simple harmonic motion (SHM).
Step 1: Identify the given values
- Mass of the block, m=4kg
- Spring constant, k=400N/m
- Initial displacement from the equilibrium position (amplitude), A=15cm=0.15m
- Displacement when calculating kinetic energy, x=−10cm=−0.1m (since it is above the equilibrium position)
Step 2: Calculate the angular frequency (ω)
The angular frequency is given by the formula:
ω=√km
Substituting the values:
ω=√4004=√100=10rad/s
Step 3: Calculate the total mechanical energy in the system
The total mechanical energy (E) in SHM is given by:
E=12kA2
Substituting the values:
E=12×400×(0.15)2=12×400×0.0225=4.5J
Step 4: Calculate the potential energy (PE) when the block is at x=−0.1m
The potential energy stored in the spring is given by:
PE=12kx2
Substituting the values:
PE=12×400×(−0.1)2=12×400×0.01=2J
Step 5: Calculate the kinetic energy (KE) when the block is at x=−0.1m
Using the conservation of energy, we know:
E=KE+PE
Rearranging gives:
KE=E−PE
Substituting the values:
KE=4.5J−2J=2.5J
Final Answer
The kinetic energy when the block is 10 cm above the equilibrium position is 2.5J.
---
- Mass of the block, m=4kg
- Spring constant, k=400N/m
- Initial displacement from the equilibrium position (amplitude), A=15cm=0.15m
- Displacement when calculating kinetic energy, x=−10cm=−0.1m (since it is above the equilibrium position)
The angular frequency is given by the formula:
ω=√km
Substituting the values:
ω=√4004=√100=10rad/s
The total mechanical energy (E) in SHM is given by:
E=12kA2
Substituting the values:
E=12×400×(0.15)2=12×400×0.0225=4.5J
The potential energy stored in the spring is given by:
PE=12kx2
Substituting the values:
PE=12×400×(−0.1)2=12×400×0.01=2J
Using the conservation of energy, we know:
E=KE+PE
Rearranging gives:
KE=E−PE
Substituting the values:
KE=4.5J−2J=2.5J
The kinetic energy when the block is 10 cm above the equilibrium position is 2.5J.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A block of mass 4kg hangs from a spring of force constant k=400N/m. The block is pulled down 15cm below equilibrium and relesed. How long does it take block to go from 12cm below equilibrium (on the way up) to 9cm above equilibrium ?
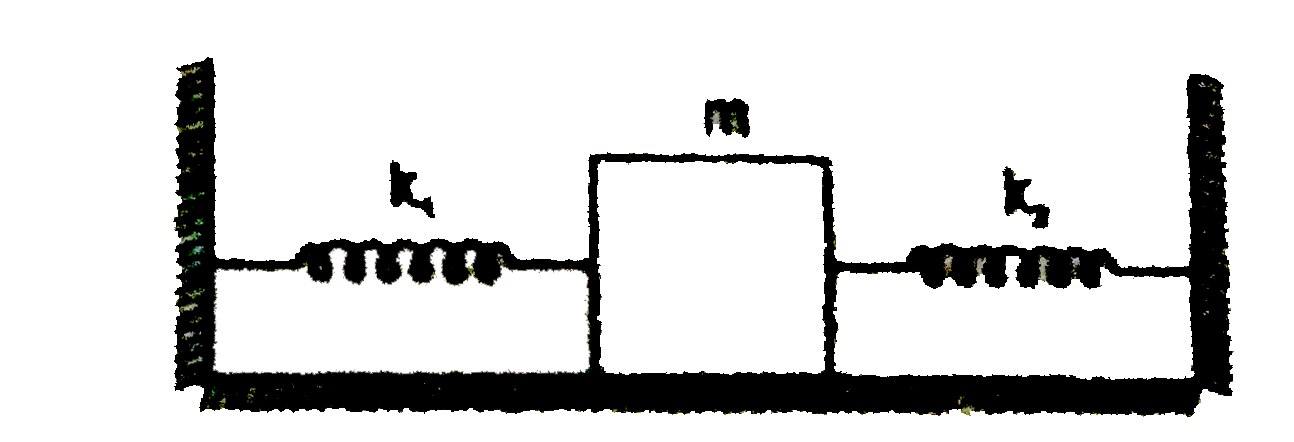
View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
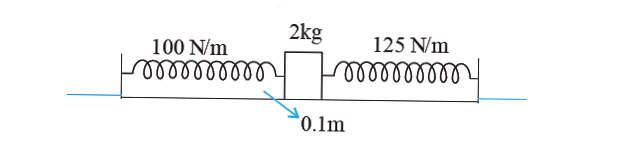
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
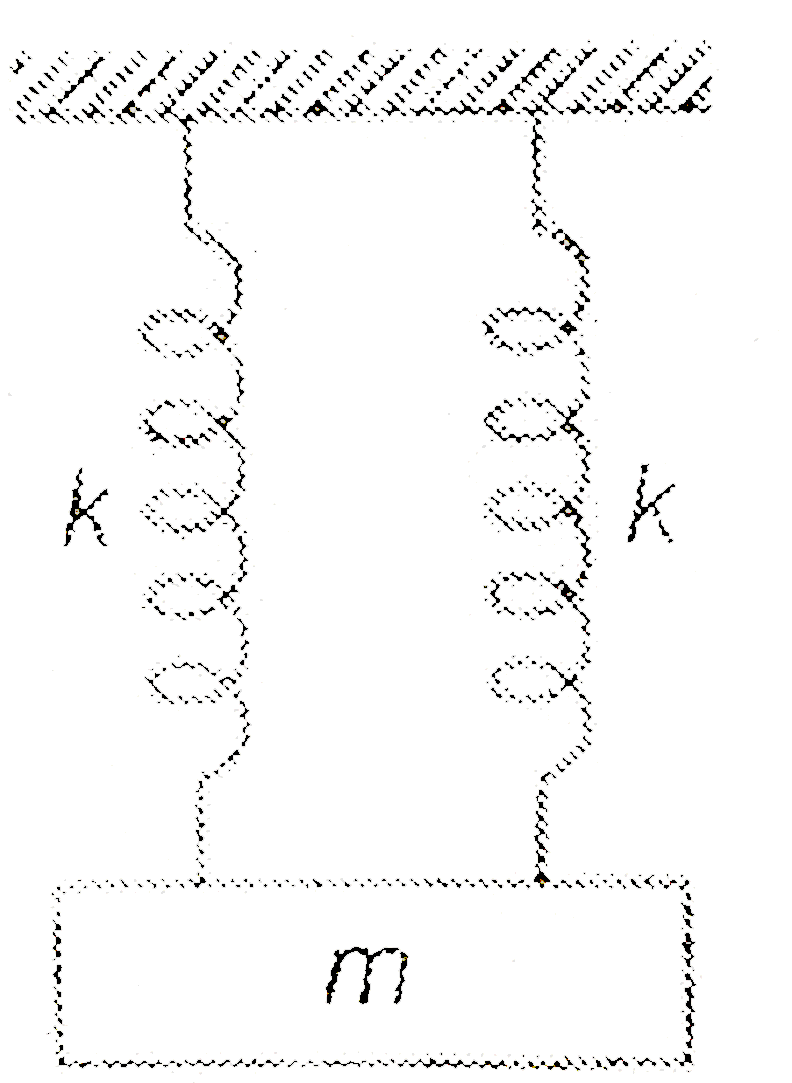
If instead of breaking one spring m/2 mass would have fallen from the block, then what will be the new amplitude?
View SolutionForce constant of a weightless spring is 16 N/m. A body of mass 1.0 kg suspended from it is pulled down through 5 cm from its mean position and the released. The maximum kinetic energy of the system (spring+body) will be (0.0x) J. Find value of x.
View SolutionPassage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
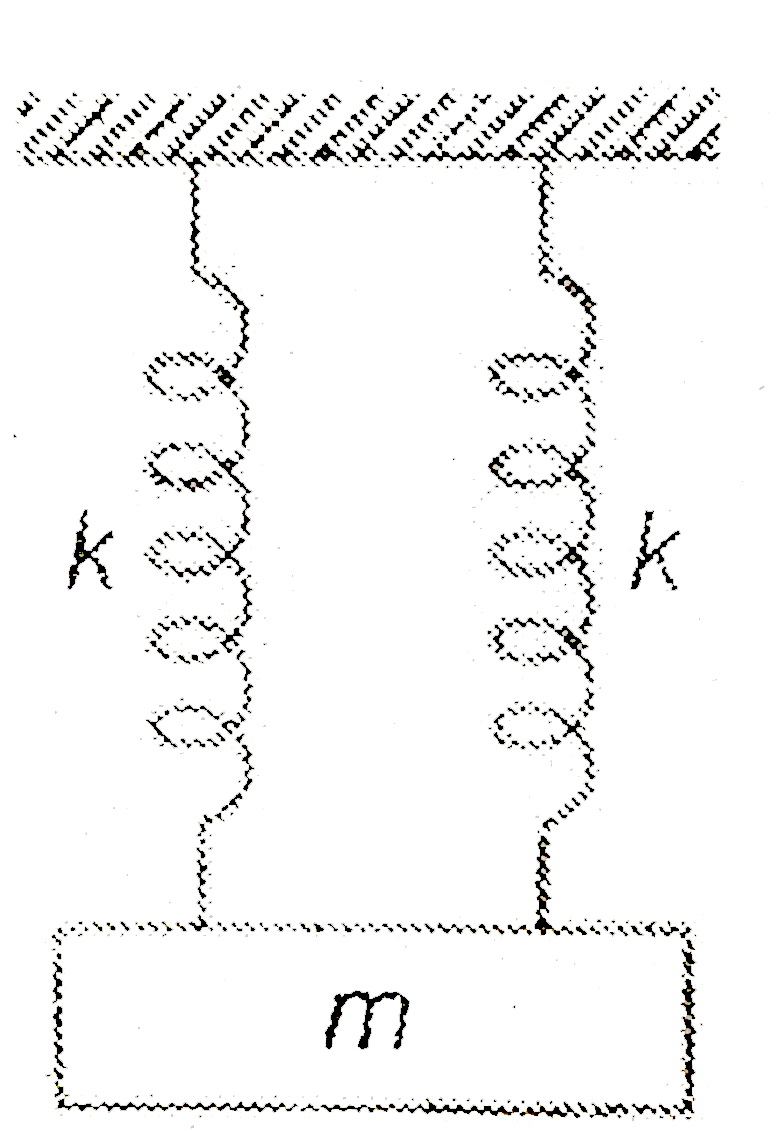
What is the new amplitude of osciallation of the block.
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_050_Q01.png)
When the block is at position A on the graph, its
View Solution