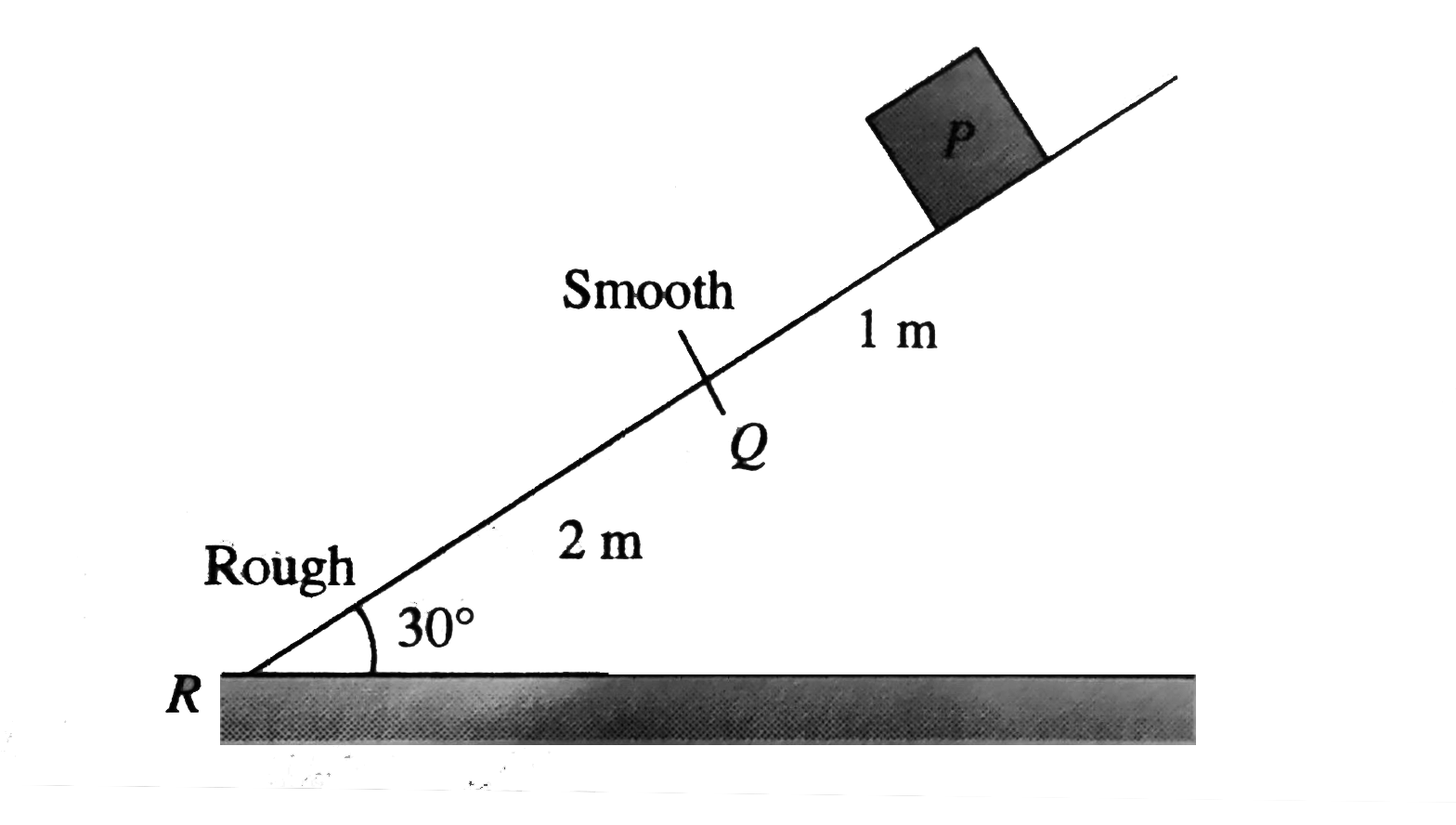
A block of mass $5.0 k g$ slides down from the top of an inclined plane of length $3 m$ . The first $1 m$ of the plane is smooth and the next $2 m$ is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at $30^{\circ}$ with the horizontal, find the coefficient of friction on the rough portion.

(a) $\frac{2}{\sqrt{3}}$

(b) $\frac{\sqrt{3}}{2}$

(d) $\frac{\sqrt{3}}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

A block of mass $m$ is released from the top of a mooth inclined plane of height $h$ its speed at the bottom of the plane is proportion to
A $m^{0}$
B $m$
C $m^{2}$
D $m^{- 1}$
What is the time required for a block to slide down from the top to the bottom ofan inclined plane 6.4 m long if the inclination of the plane with the horizonta l is 30° and the coefficient of friction= 0.2?
A2s
B1.5s
C3s
D2.5s
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
A $m^{0}$
B $m$
C $m^{2}$
D $m^{- 1}$