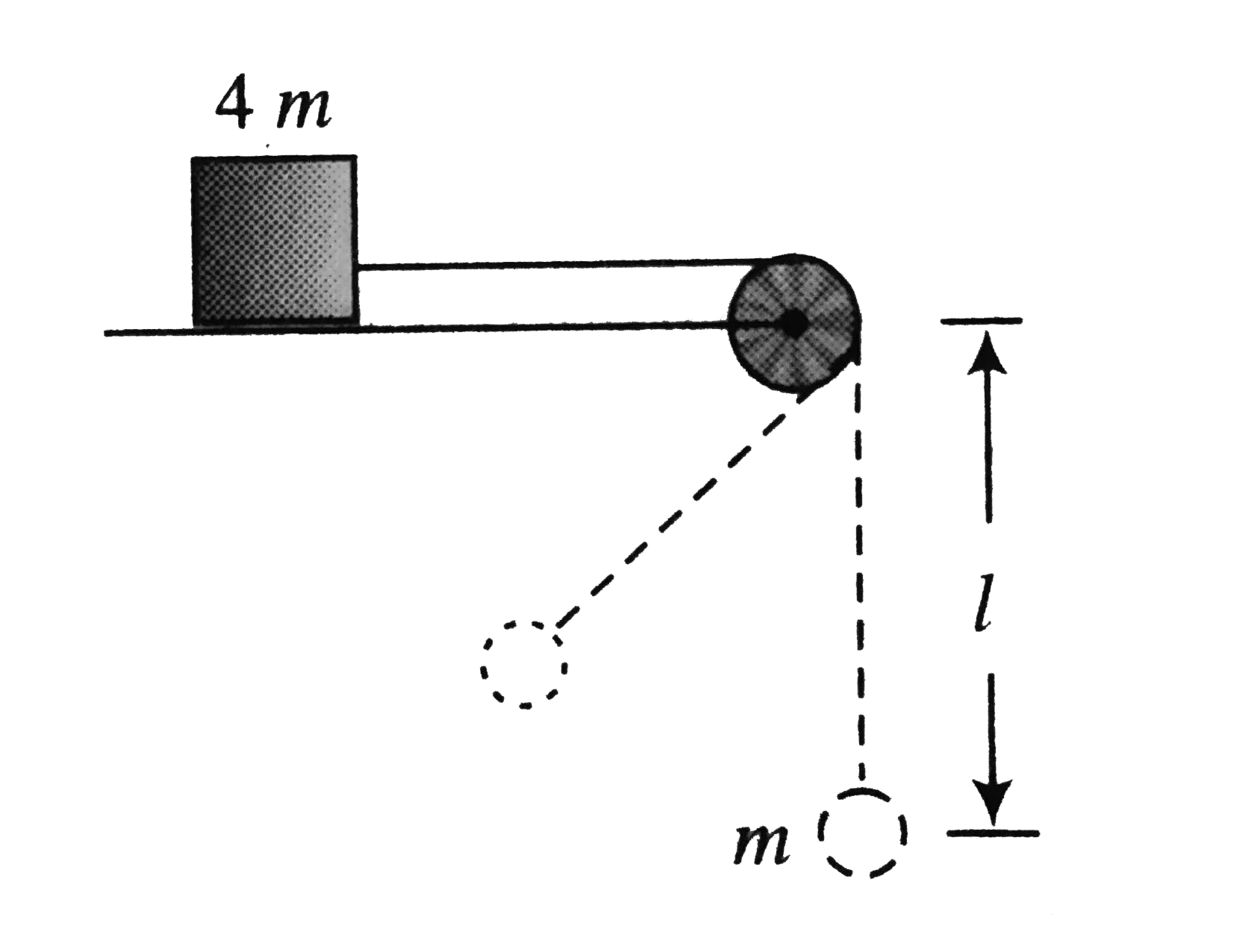
Two bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)
(a) 14
(b) 34
(c) 12
(d) 18
The correct Answer is:C
Velocity at lowest position =√2gl(1−cos60∘)=√gl
T=mg+mV2l=mg+mlgl=2mg
∴T=μ4mg⇒12
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
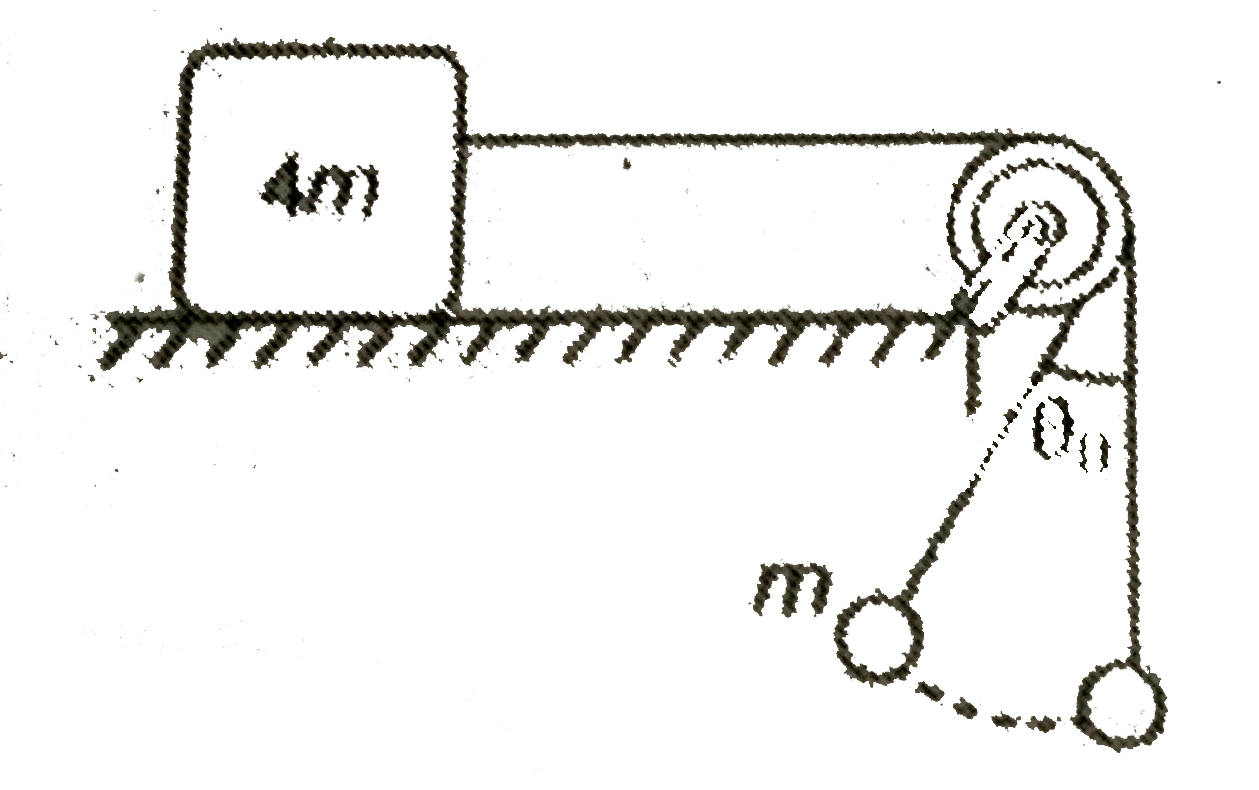
Two bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04) - Question 2 - Select One
Two bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is :
 A14(1−A2l2)B14(1+A2l2)C14AlcosθD14
A14(1−A2l2)B14(1+A2l2)C14AlcosθD14 - Question 3 - Select One
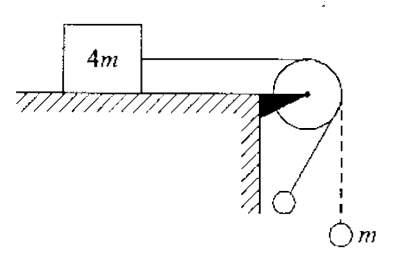
Two bodies of mass m and 4m are attached with string of length l is excurting oscillations of angular amplitude θ0 while the other body is at rest . The minimum coefficient of friction between the mass 4m and the horizontal surface should be:
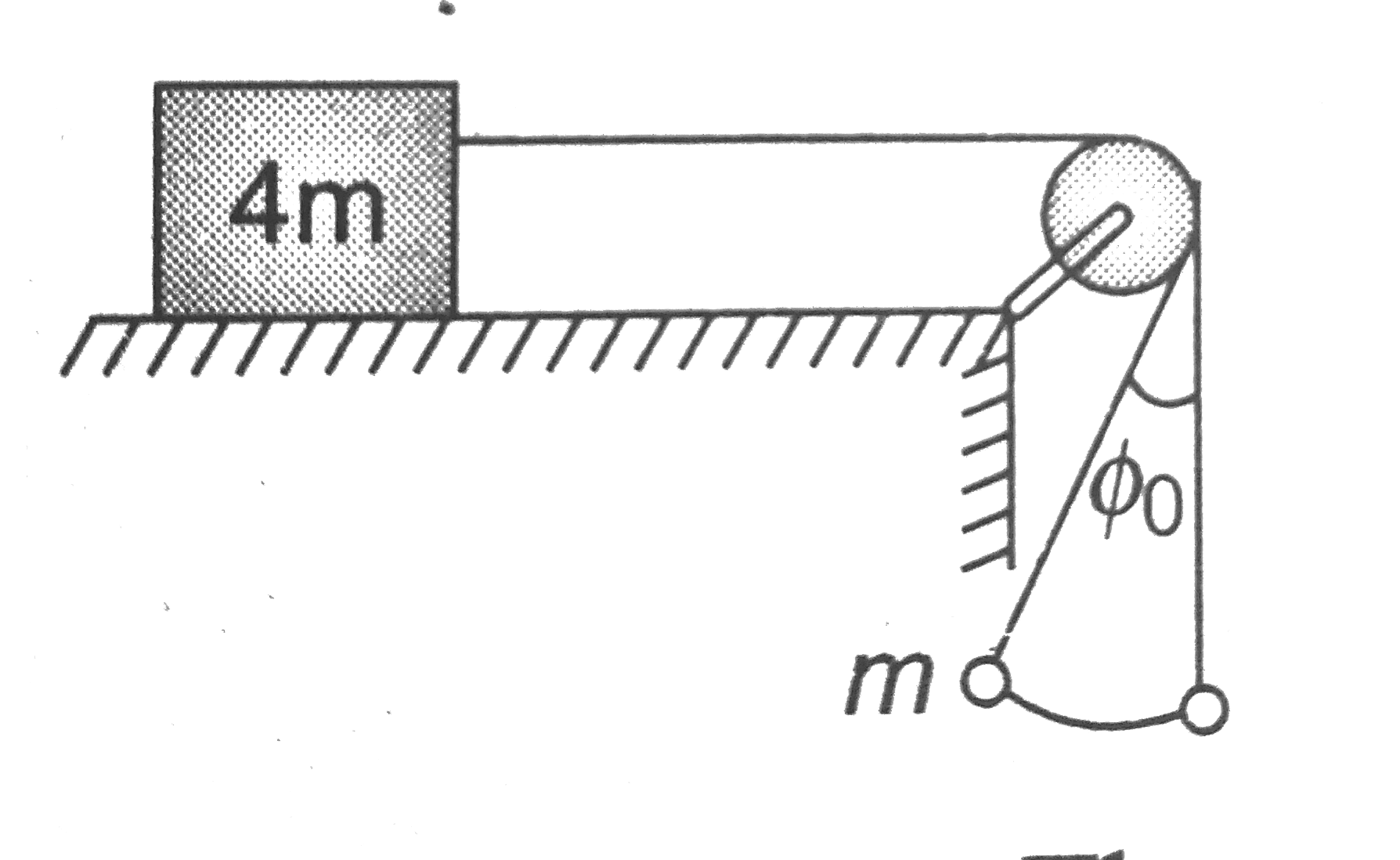 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04)
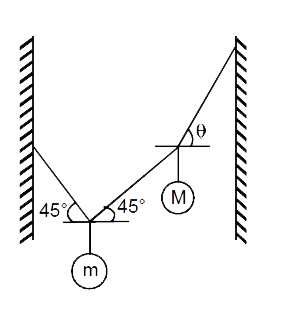
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
 View Solution
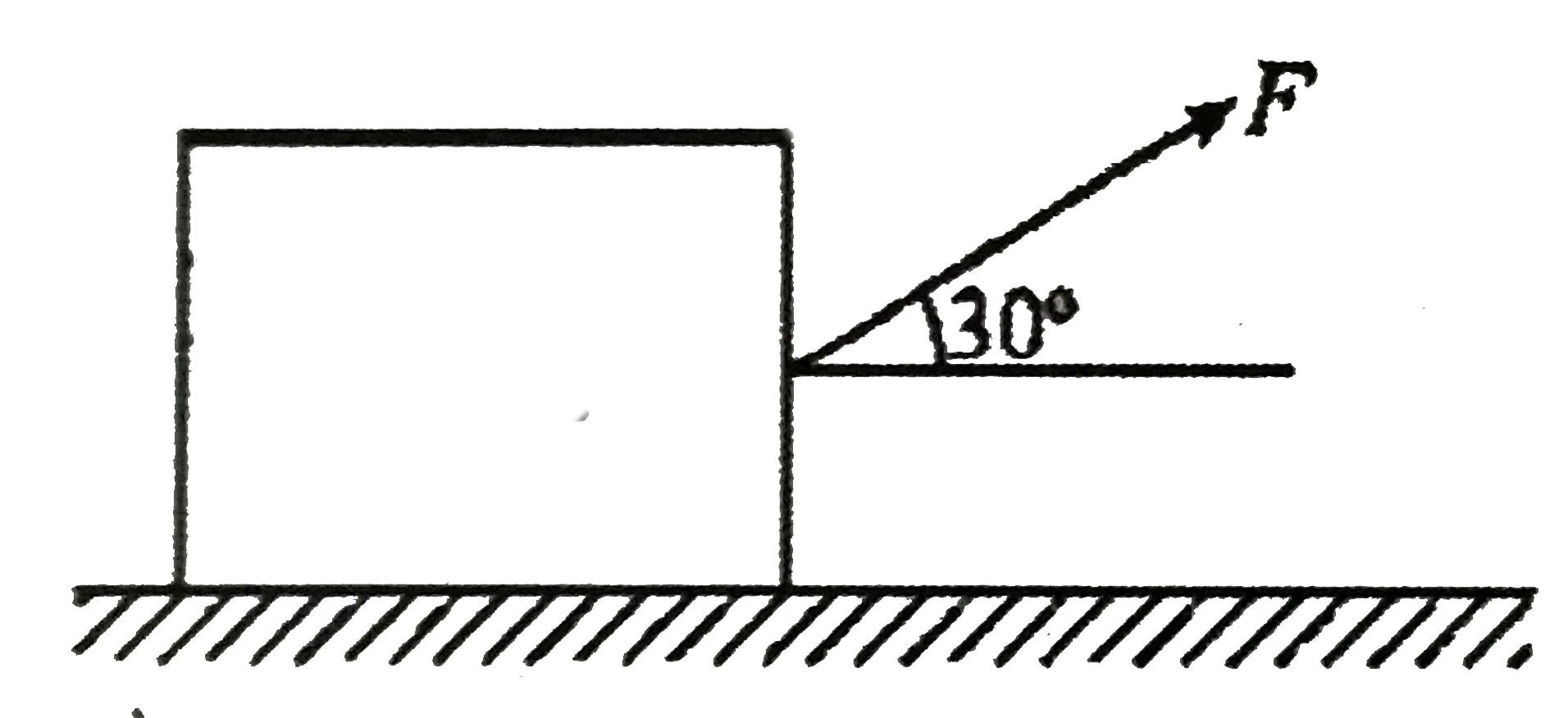
View SolutionA mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
 View Solution
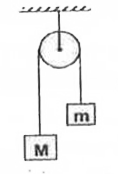
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 View Solution
View SolutionA body of mass m, having momentum p, is moving on a rough horizontal surface. If it is stopped in a distance x, the coefficient of friction between the body and the surface is given by
View SolutionTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
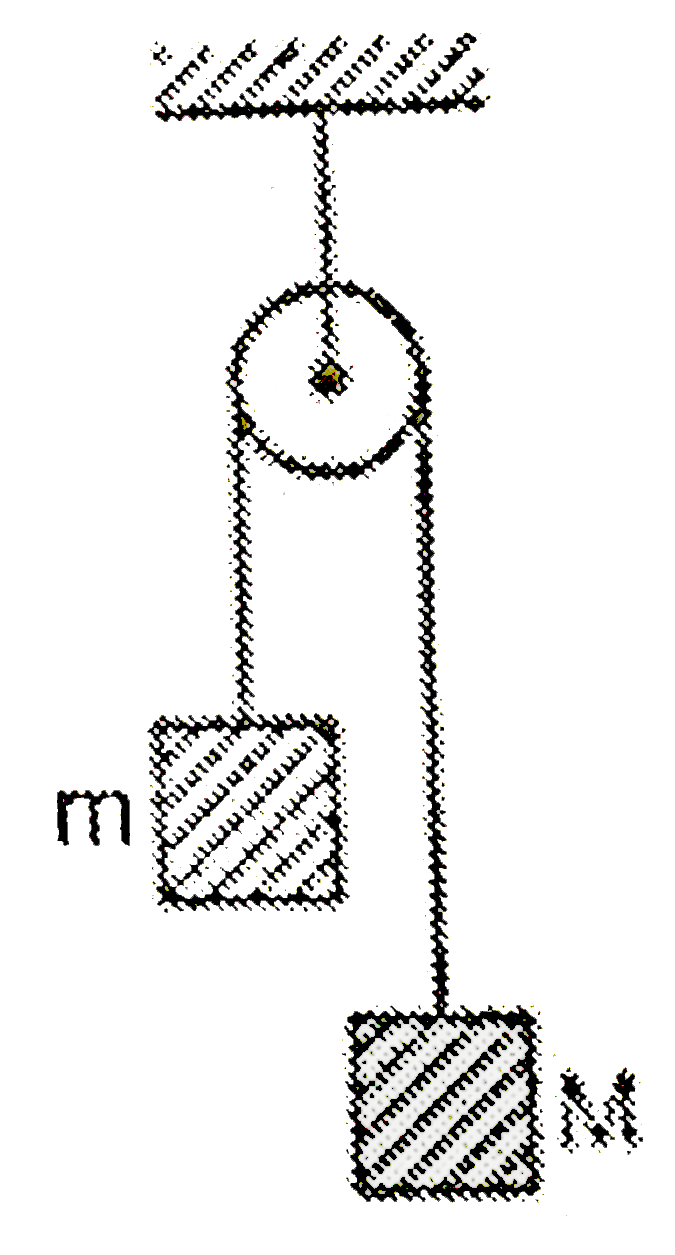 View Solution
View Solution