A block of mass m and density p is hanging from a string . If it is lowered into a vessel of cross-sectional area A containing a liquid of density σ(<ρ) and gets fully immered, the increase in pressure at the bottom of vessel would be
mρgσA
mρgρA
mgA
zero
Volume of block =mρ
∴ Boutant force on block - Volume × Density of liquid ×g=mρ×σ×g
By Newtom's third law of motion, force exerted by block on liquid surface =mσgρA
∴ Increases in pressure =mσgρA
Topper's Solved these Questions
- FLUID MECHANICSBOOK - BITSAT GUIDECHAPTER - FLUID MECHANICSEXERCISE - BITSAT Achives
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - BITSAT GUIDECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - All Questions
33 Videos
- GAUSS LAW AND ELECTRIC POTENTIAL THEORYBOOK - BITSAT GUIDECHAPTER - GAUSS LAW AND ELECTRIC POTENTIAL THEORYEXERCISE - BITSTAT ARCHIVES
4 Videos
Similar Questions
Knowledge Check
A cylinder of mass m and density ρ hanging from a string is lowered into a vessel of cross-section area s containing a liquid of density σ(<ρ) unit it is fully immersed. The increase in pressure at the bottom of the vessel is
AmρgσsBmgsCmσgρsDzeroA cylinder of mass M and density d1 hanging from a string, is lowered into a vessel of cross-sectional area A, containing a liquid of density d2(d2<d1) until it is fully immersed. The increase in pressure at the bottom of the vessel is
AMd2gd1ABMgACMd1gd2ADzeroTwo vessels A and B of cross sections as shown contain a liquid up to the same height. As the temperature rises, the liquid pressure at the bottom (neglecting expansion of the vessels ) will :
 AIncrease in A , decrease in BBincrease in B , decrease in ACIncrease in both A and B but more in ADIncrease in both A and B equally
AIncrease in A , decrease in BBincrease in B , decrease in ACIncrease in both A and B but more in ADIncrease in both A and B equally
A wooden block or mass m and density ρ is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density σ with σ>ρ. The tension in the string will be
View SolutionIf a vessel containing a fluid of density ρ upto height h is accelerated vertically downwards with accelerations a0. Then the pressure by fluid at the bottom of a vessel is
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

View SolutionA block of silver of mass 4kg hanging from a string is immersed in a liquid of relative density 0.72. If relative density of silver is 10, then tension in the string will be
View SolutionFigure here shows the vertical cross-section of a vessel filled with a liquid of density ρ. The normal thrust per unit area on the walls vessel at point. P, as shown, will be
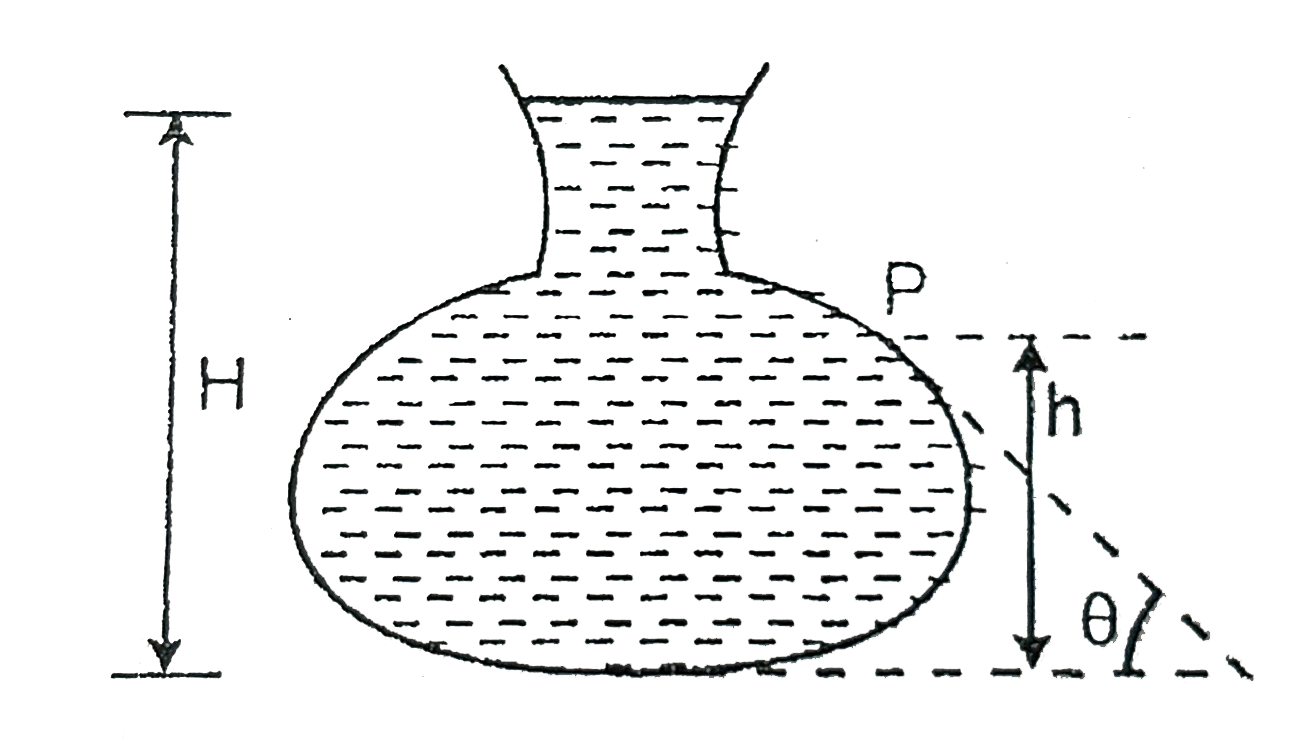
View Solution
