A block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
Let the force applied by string to the block be T. For part (a), consider one system is block and other string. Let the acceleration of the system (block +string) be a.
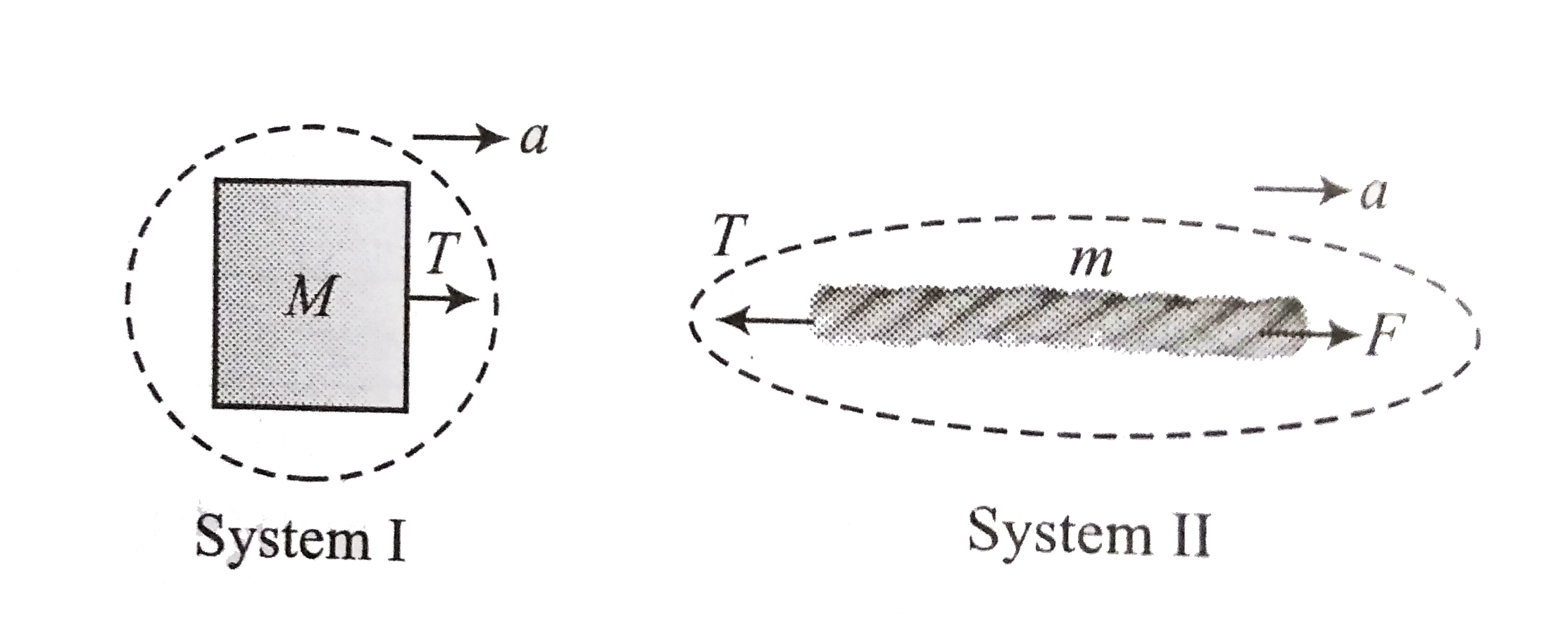
Now we apply Newton's law to each of them.
For system II: F-T=ma ...(i)
For system I:T=ma...(ii)
After solving (i) and (ii), a=FM+m,T=MFM+m
(b) Now we have to redefine our system. Choose system 1 as block and half string and system 2 as the other half string . On applying Newton's second law to system 1 and system 2, we have
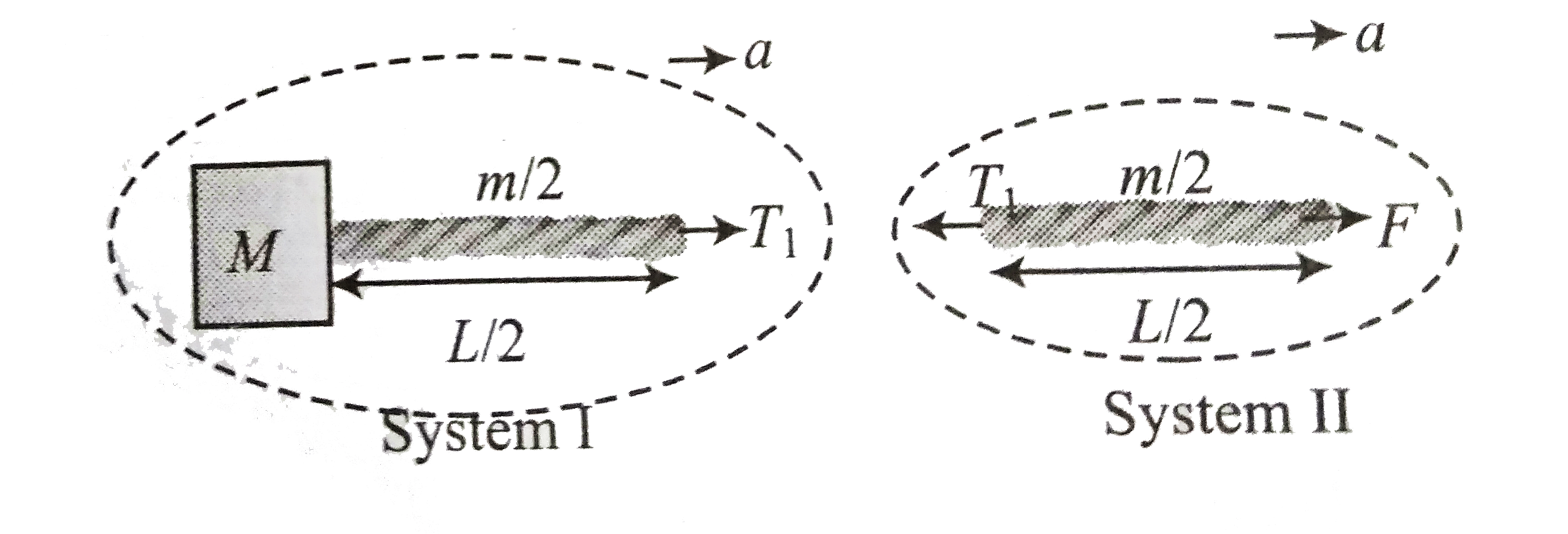
System II: F=(T1)=m2×a ...(iii)
Mass per unit length of string =m/L
Hence, mass of L/2 length of string mL×L2=m2
System I: T1=(M+m2)a...(iv)
After solivng (iii) and (iv) we get,
a=FM+m,T1=(M+m/2)F(M+m)
c. Now we can redefine our system in the block and string of length L-x(system I) and string of length x (system II)

System II: F−T2=(mL×x)a ...(v)
System I: T2={mL(L−x)+M}a ...(vi)
Solving (v) and (vi) we get
a=FM+mand(T2)={m(L−x)/L+M}FM+m
Here we see that acceleration in each part is same, but tension changes along the string.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Knowledge Check
- Question 1 - Select One
A body of mass M is being pulled by a string of mass m with a force P applied at one end. The force exerted by the string on the body is
APm(M+m)BPM(M+m)CPm(M+m)DP(M−m) - Question 2 - Select One
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBF should be equal to the weight of A and BCF(L-x)/LDF(L-x)M - Question 3 - Select One
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mg
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point
 View Solution
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.
 View Solution
View SolutionIn the following figure, the object of mass m is held at rest by a horizontal force as shown. The force exerted by the string on the block is -
 View Solution
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View Solution



