A block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
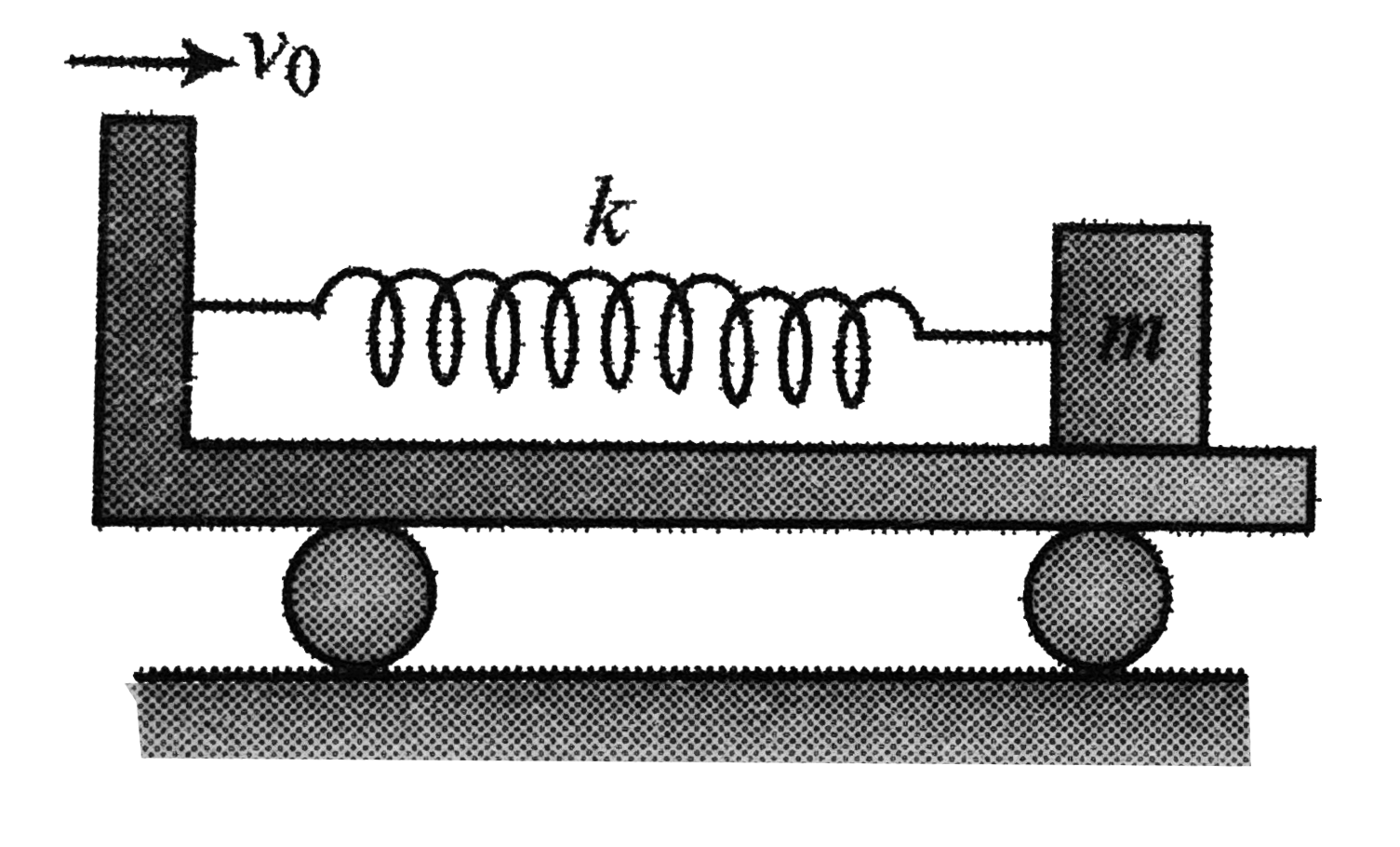
Let us take wedge+spring+block, as a system. The forces responsible for performing work are spring force kx(←) and the external force F(→).
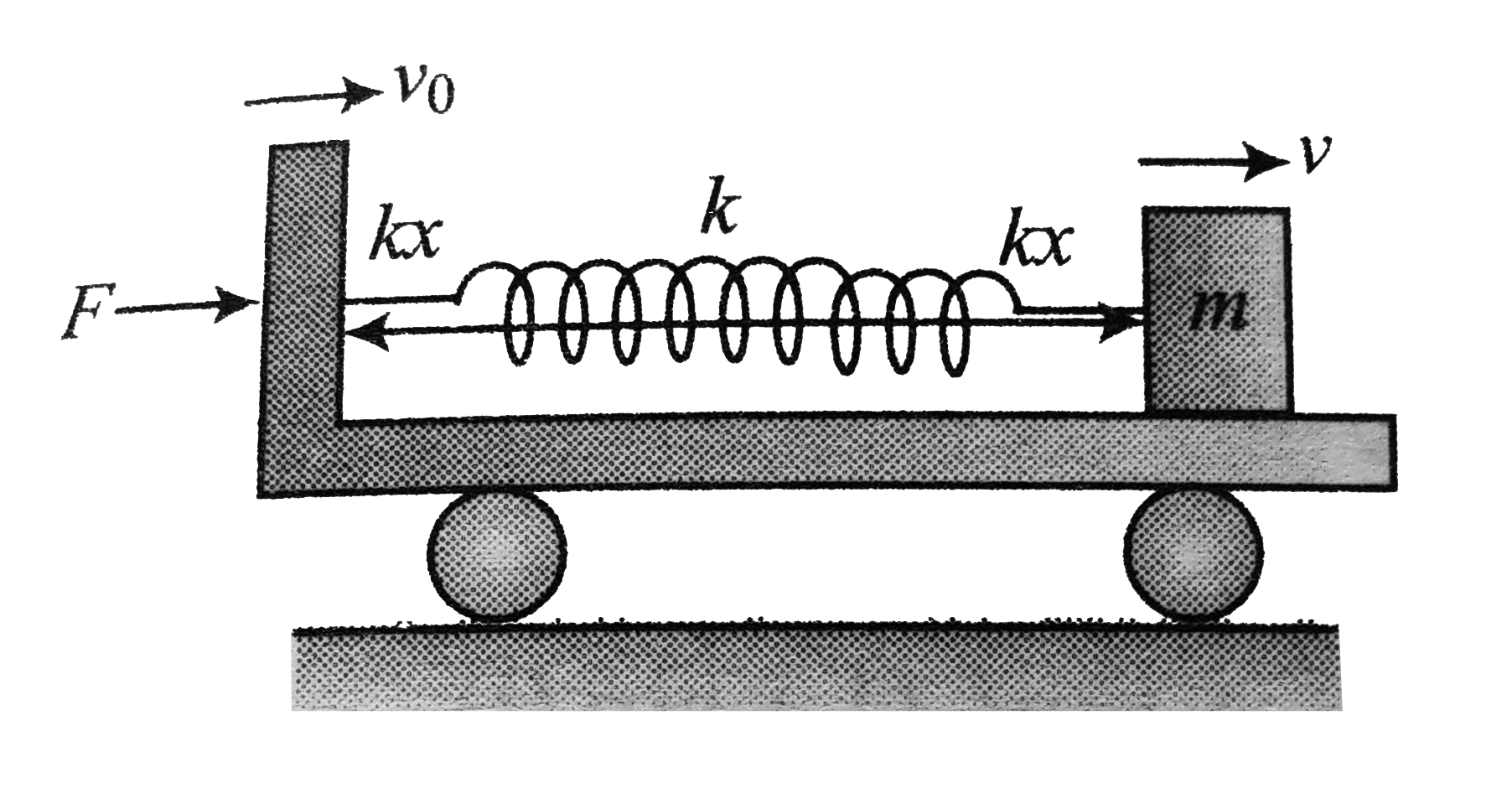
Applying W−E theorem for block+spring+plank relative to ground:
We have Wext+Wsp=ΔK,
Where Wsp the total work done by the spring on wedge and block =−12kx2 and ΔK is the change in KE of the block (because the plank does not change its kinetic energy).
Then, Wext=12kx2+ΔK
As the block was initially stationary, it will acquire a velocity v0 equal to that of the plank at the time of maximum compression of the spring. The change in kinetic energy of the block relative to ground is
ΔK=12mv20
Substituting ΔK in the above equation, we have
Wext=12kx2+12mv20
Applying W−E theorem for block+spring+plank relative to the plank:
Now we need to find x. For this, let us climb onto the plank. Since the plank moves with constant velocity, there is no pseudo force acting on the block. Then the net work done on the system (block+plank) is due to the spring, can be given as
Wsp=−12kx2
As the relative velocity between the observer (plank) and block decrease from v0 to zero at the time of maximum compression of the spring, the change in kinetic energy of the block is
ΔK=−12mv20. Applying work-energy theorem, we have
W=ΔK, where W=−12kx2 and ΔK=−12mv20
This gives 12kx2=12mv20
Substituting 12kx2=12mv20 from Eq. (ii) and Eq. (i), we have
Wext=mv20
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.
View SolutionA block of mass m is slowly lowered from a point where it just touches a vertical fixed spring of stiffness k, till it remains stationary after the applied force is withdrawn. Find the work done by the external agent(a) in compressing the spring by a distance x and (b) bringing the block to its stable equilibrium position.

View SolutionA block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.

View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
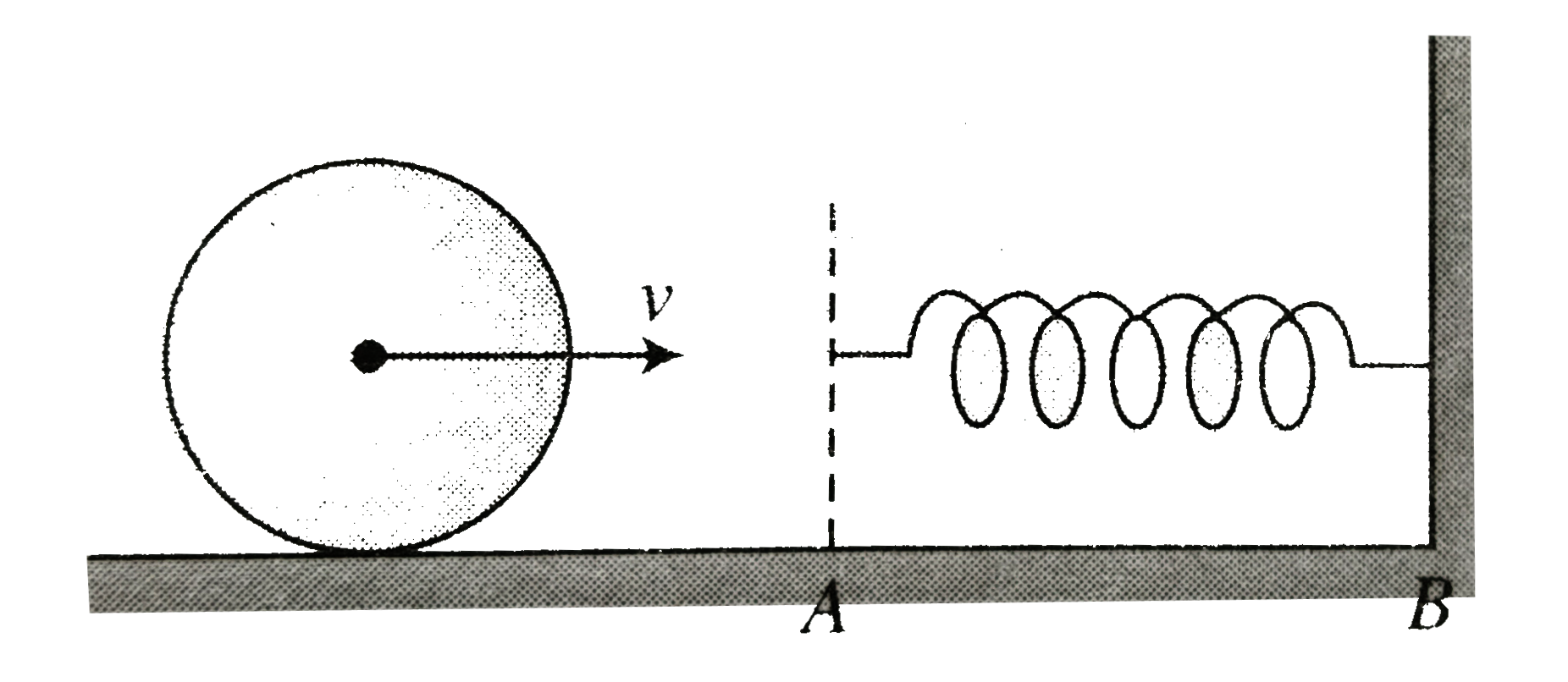
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.

a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth plane .find the value of spring force .
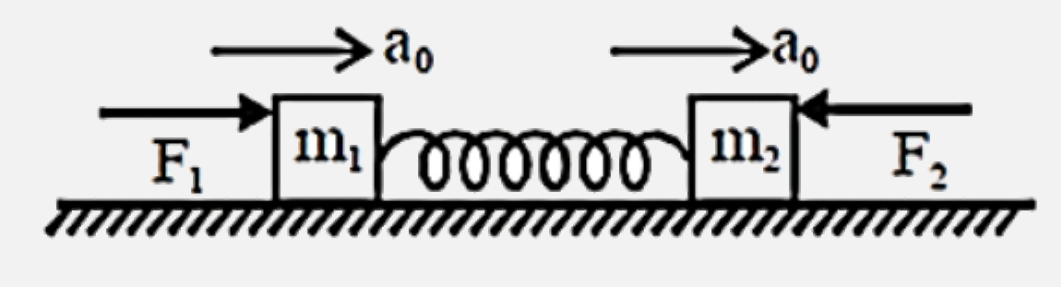
View SolutionA block of mass m moving with a velocity v0 on a smooth horizontal floor collides with a light spring of stiffness k that is rigidly fixed horizontally with a vertical wall. If the maximum force imparted by the spring on the block is F, then:
(A) F∝√m (B)F∝√k
(C) F∝v0 (D) None of these
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
View Solution