A block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?Solution in Tamil
Let P bet he force applied to it an angle θ From the free body diagram,
R+Pisnθ−mg=0
→R=−Ψnθ+mg……….i
μR=Pcosθ……….ii
From equation i
μ(mg−Ψnθ)−Pcosθ
μmg=μΨnθ−Pcosθ
→P=μmgμsinθ+cosθ
Applied force Pshould be minimum, when msinθ+cosθ is maximum.
Again (μsinθ+cosθ) is maximum when its derivative is zero
ddthη(μsinθ+cosθ)=0 rarr mucostheta-sintheta=0<br>→theta=tan^-1 mu<br>So,P=(mumg)/(musintheta+costheta)<br>=(mumg/costheta)/((musintheta)/(costheta)+(costheta)/(costheta))<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C06_E01_046_S01.pngwh=80%mx-autosty≤=background:white;><br>(DivgNumera→randDenomiNA→rbycostheta), we get
P=μmgsecθ1+μtanθ
μmgsecθ1+tan2θ=μmgsecθ
=μmg√1+tan2θμmg1+μ2
Hence minimum fore is μmg√1+μ2 at an angle θ=tan−1μ
Topper's Solved these Questions
Similar Questions
Let F,FNandf denote the magnitudes of the contact force, normal force and the friction exerted by one surface on the other kept in contact. If none of these is zero,
View SolutionWater is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
View SolutionTwo spherical balls of mass 10 hg are placed 10 cm apart. Find gravitational force of attraction between them
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass 70kg is kept on a rough horizontal surface (mu=0.4) . A person is trying to pull the block by applying a horizontal force, but the block is not moving. The net contact force exerted by the surface on the block is F , then:
View SolutionA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
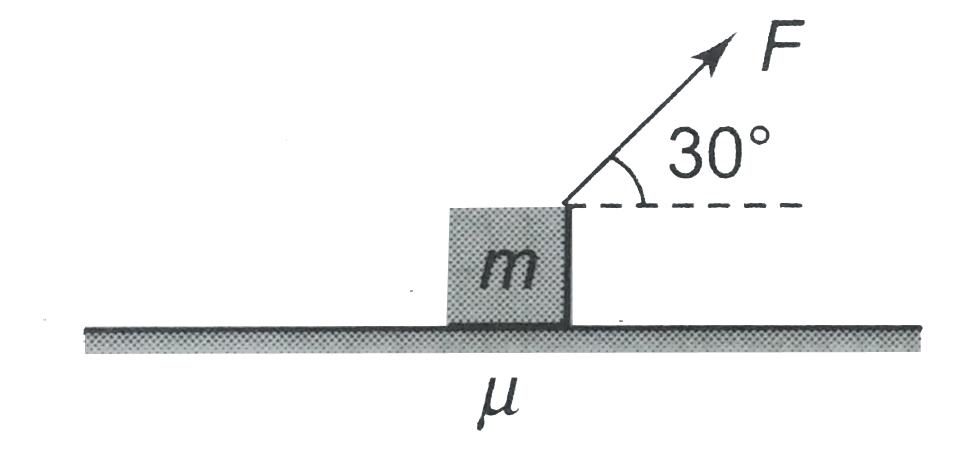
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View SolutionA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
View Solutionएक खुरदरी क्षैतिज सतह पर M द्रव्यमान का एक गुटका रखा हुआ है| गुटके तथा सतह के बीच स्थितिज घर्षण गुणांक μ है|गुटके को एक बल लगाकर खींचा जा रहा है| गुटके को खिसकाने के लिय न्यूनतम कितना बल आवश्यक है? यह बल किस दिशा में लगाया जाना चाहिए?
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction mu. A force is applied to the block at an angle theta with the horizontal. The block will move with a minimum force F if
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
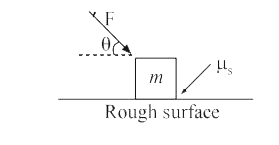
View SolutionA block of mass 70 kg is kept on a rough horizontal surface and coefficient of static friction between block and surface is 0.4 . A man is trying to pull the block by applying a horizontal force .The net contact force exerted by the surface on the block is F , then:
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View Solution
