Question

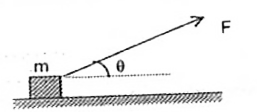
A block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle $\theta ={37}^{\circ }$, with horizontal as shown in fig. find the acceleration of the block at the given instant.

Options

A. `5sqrt(5) g`
B. `3sqrt(5) g`
C. `2sqrt(3) g`
D. `2sqrt(5) g`

Answer

D

Explanation

Three forces act on the block (a) `mg darr (b) F=5mg (c ) N uarr`

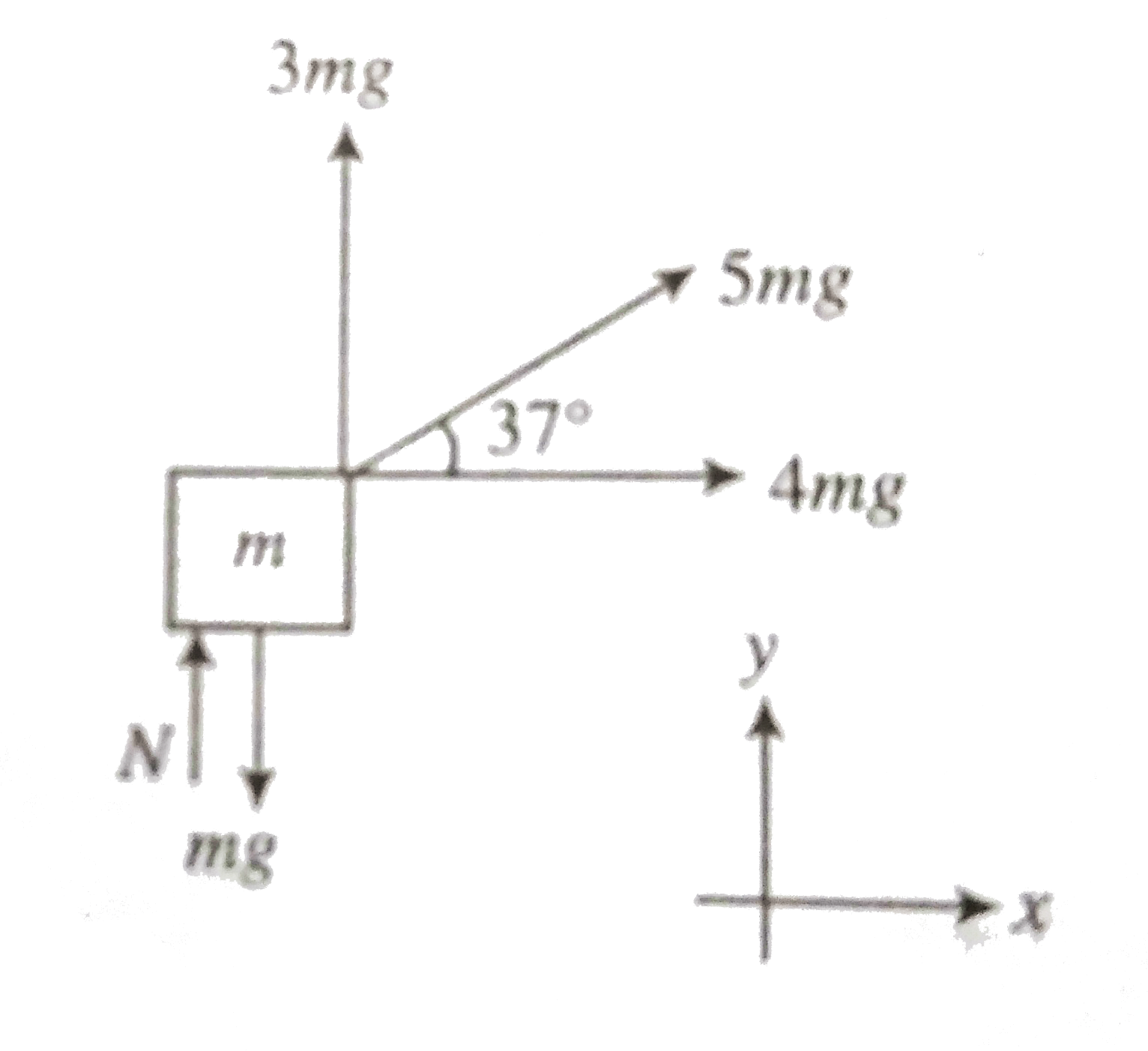
Resolving the forces along x- and y-axis, we have equation of motion.
`Sigma F_(x)=ma_(x)`
`4mg=ma_(x)`
This gives`a_(x)=4g` ...(i)
`Sigma F_(y)=ma_(y)`
`3mg-mg +N = ma_(y)`
`2mg+N = ma^(y)` ..(iii)
Let `a_(y)=0. Then N=-2mg`
The nagative result signifies that N will be directed down (opposite to assumed direction), but the ground cannot pull the block down. Hence, the block will lose contact with the ground.
or `N=0`
Hence, from (ii) , `a_(y)=2 g uarr`
Hence, the acceleration , `|vec(a)|=sqrt(a_(x)^(2)+a_(y)^(2))`
Where `a_(x)=4g` form eq. (i) and `a_(y)=2g` from eq. (ii)
This gives `a=sqrt(a_(x)^(2)+a_(y)^(2)) = sqrt((4g)^(2)+(20)^(2))=2sqrt(5) g` .