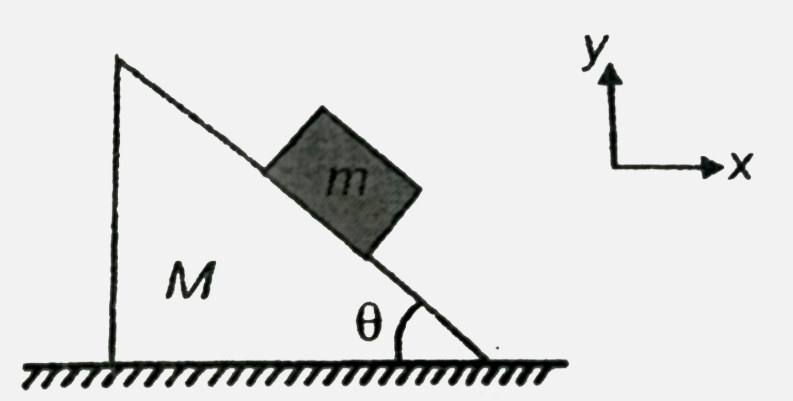
A block of mass m is placed on a smooth inclined wedge ABC of inclination as shown in the figure.

The wedge is given an acceleration a towards the right. The relation between a and e for the block to remain stationary on the wedge is
a=gcosecθ
a=gsinθ
a=g cos theta
a=gtanθ
The correct Answer is:D
In non-inertial frame ,
Nsinθ=ma….. (I )
Ncosθ=mg………(ii)
from (I ) and (ii)
tanθ=ag
a=gtanθ

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - CHECK YOUR NEET VITALS
22 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
Similar Questions
Knowledge Check
A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
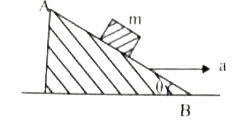 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is
 AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than m
AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than m
A block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
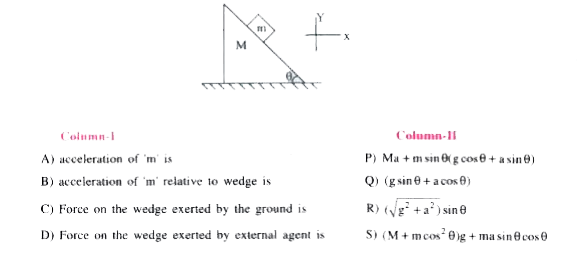
View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View SolutionA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is

View SolutionA block of mass m is placed on a wedge of mass M. Coefficient between then is μ<cotθ. The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge.

View SolutionA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
View Solution