A block of mass m is placed on the block of mass M as shown in figure. The horizontal force →F acts on M during time interval t. If the horizontal surface is smooth, assuming no relative sliding between the blocks, find the
a. work done by friction on the blocks
b. work done by →F on the lower block
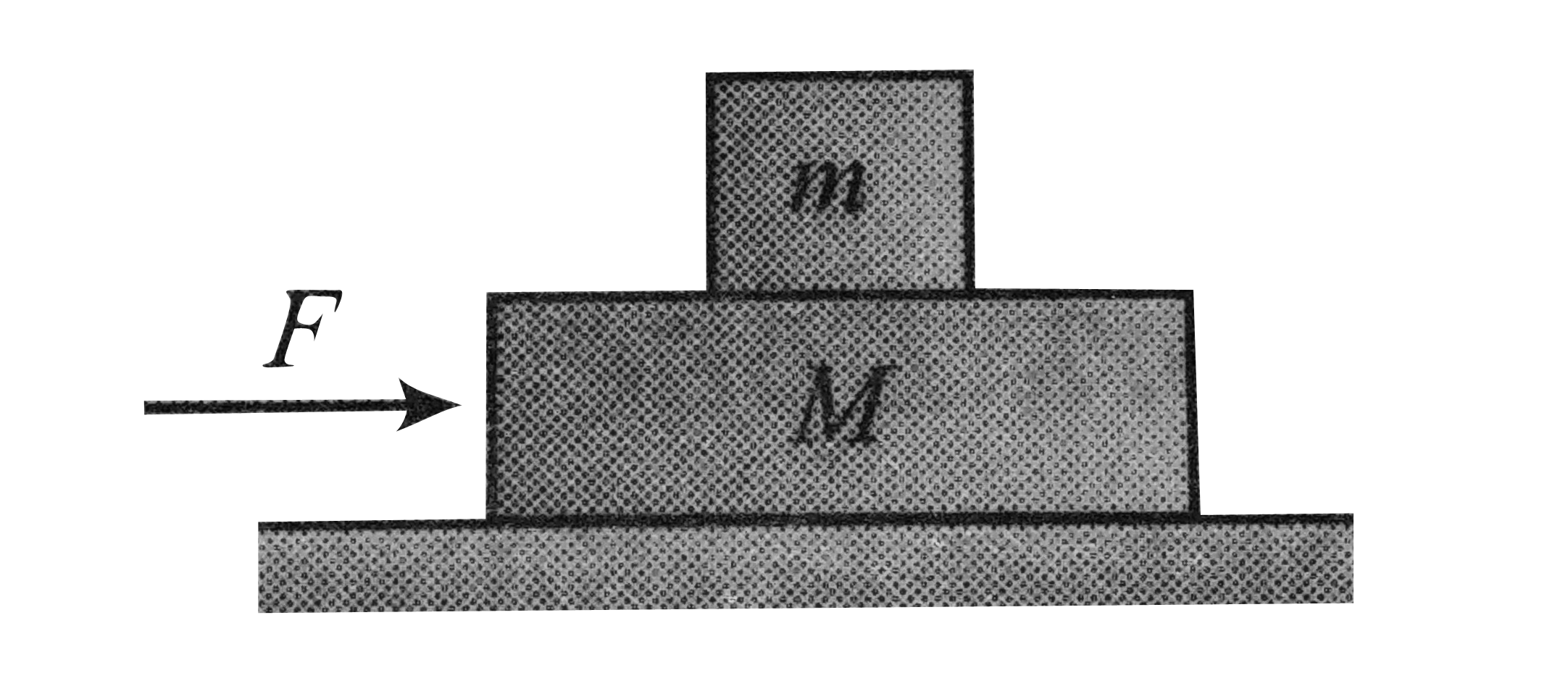
a. As there is no relative sliding between the blocks, they move with a common acceleration,
a=FM+m
Then the static frictional force on the block m is
f=ma, where a=FM+m. Then
f=mFM+m
Work done by static frictional force on the block m
Since (Wf)m=→f.→s=fscos0∘=fs
where s=12at2
We have (Wf)m=f(12at2)
Substituting f=mFM+m and a=FM+m
We have (Wf)m=mF2t22(M+m)
As no relative sliding between m and M, hence, net work done by static friction is zero.
Since (Wf)m+(Wf)M=0
Hence, the work done by the static frictional force on the block m
We have (Wf)m=mF2t22(M+m)
b. The displacement of lower block during time t,
⇒s=12(FM+m)t2
Hence, work done by F, WF=→F.→s
WF=F⋅s=F[12(FM+m)t2]=F2t22(M+m)
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is kept over another block of mass 2m and the system rests on a smooth horizontal surface. The coefficient of friction between the block is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement the of the system when a force mg is applied to the lower block
View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

View Solution
Knowledge Check
A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
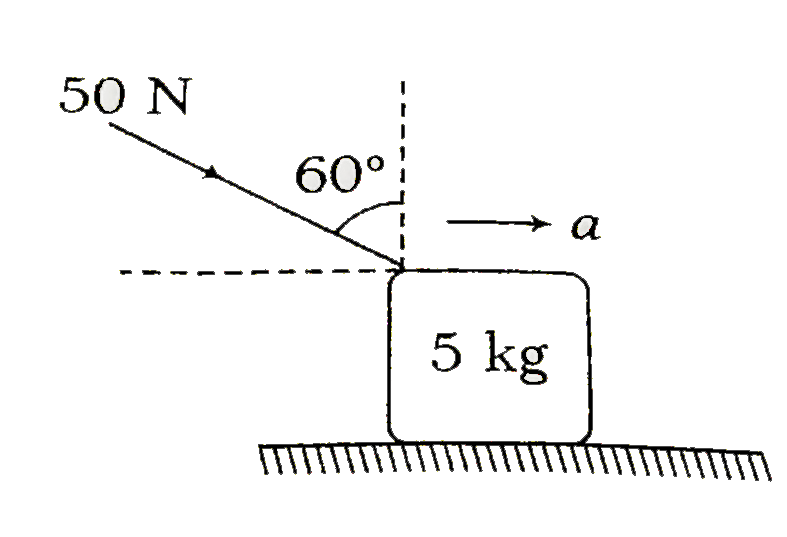 A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A bullet of mass 'm' moving with velocity 'u' passes through a wooden block of mass M=nm as shown in figure. The block is resting on a smooth horizontal floor. After passing through the block, velocity relative to the block is
 .
.
View SolutionA block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
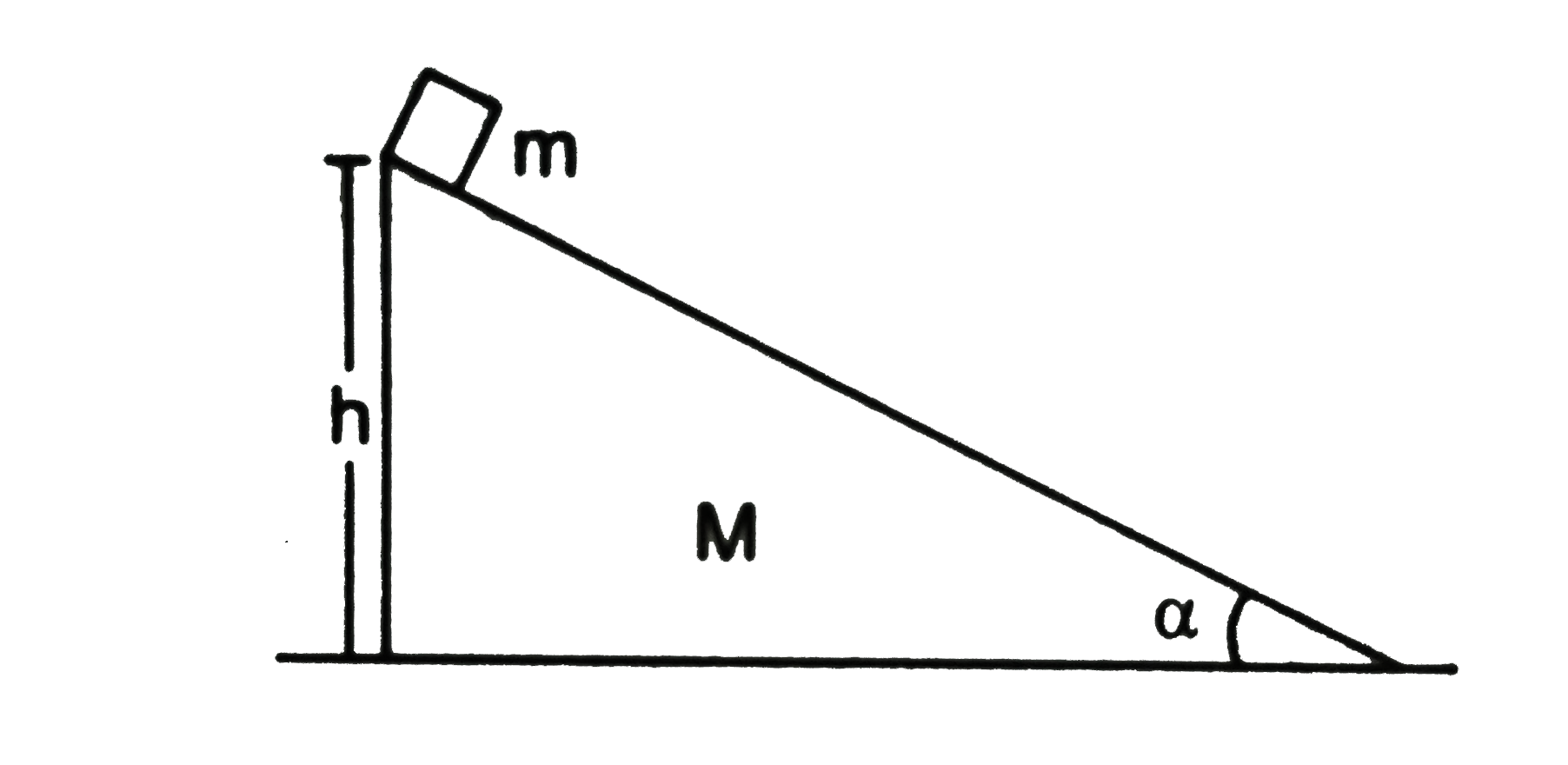
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionA small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
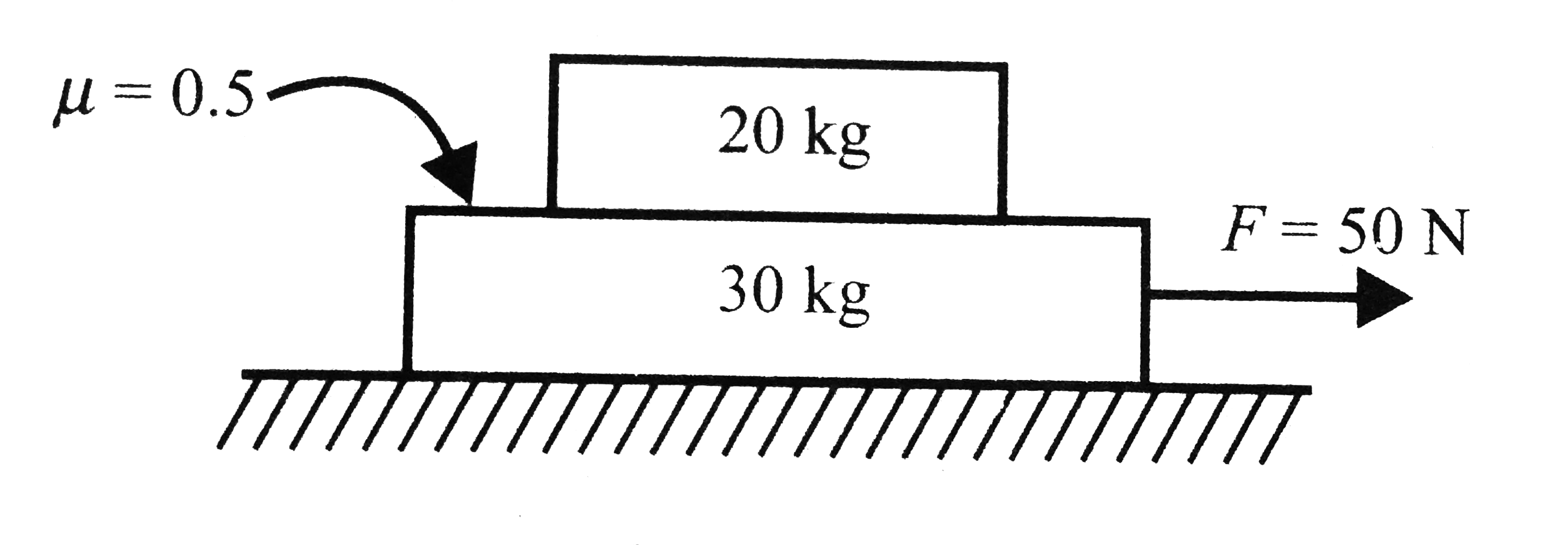
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?
View SolutionBlock B of mass m has been placed on block A of mass 3 m as shown. Block A rests on a smooth horizontal table. F1 is the maximum horizontal force that can be applied on the block A such that there is no slipping between the blocks. Similarly, F2 is the maximum horizontal force that can be applied on the block B so that the two blocks move together without slipping on each other. When F1andF2 both are applied together as shown in figure.

(a) Find the friction force acting between the blocks.
(b) Acceleration of the two blocks.
(c) If F2 is decreased a little, what will be direction of friction acting on B.
View SolutionA bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block

View Solution
