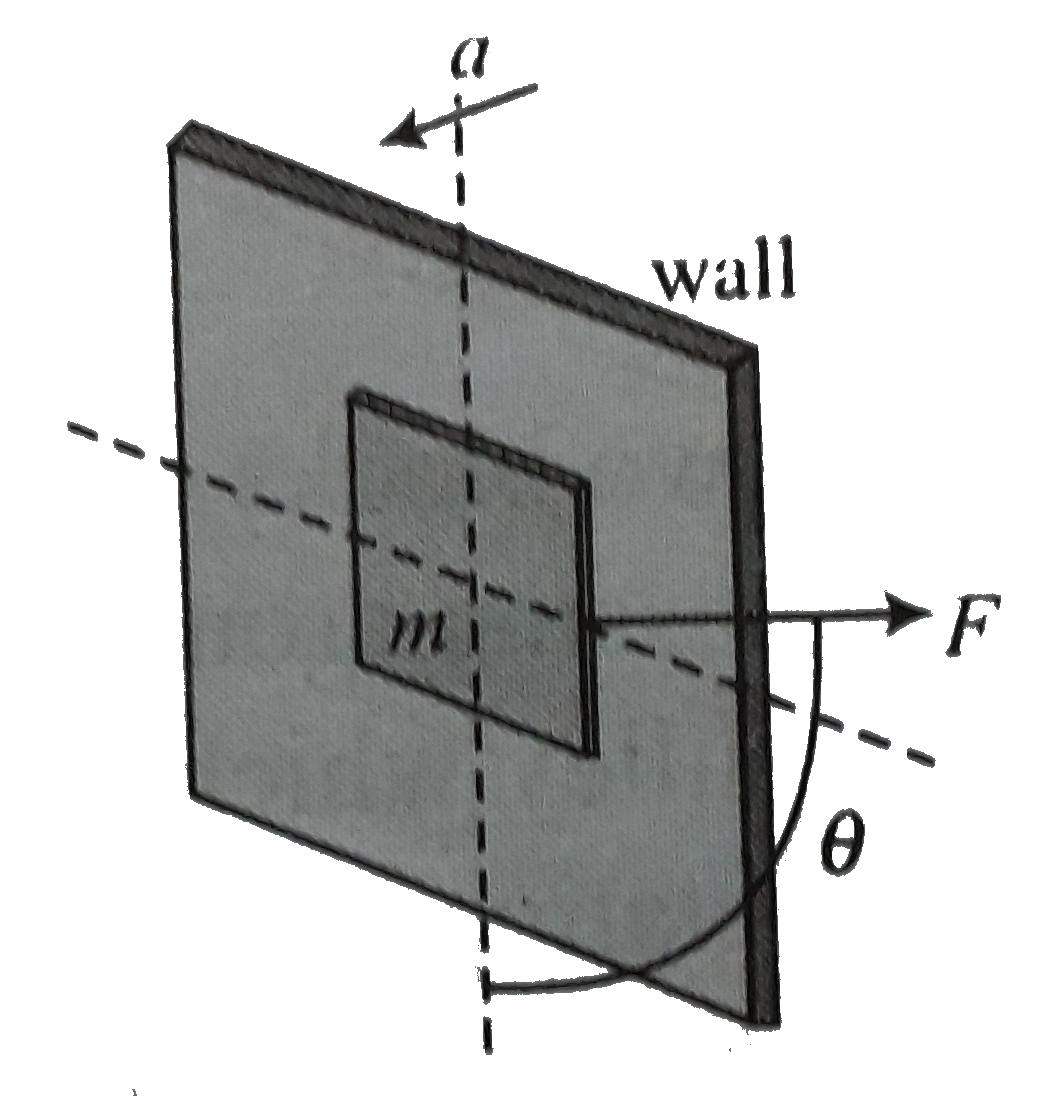
A block of mass m is pressed against a wall which is moving with an acceleration a as shown in figure If the block is pulled at an angle θ with downward vertical by a force F and it does not slide relative to the wall . Find the
a. friction force between the block and wall
b.inimum magnitude of F so as to cayse a relative sliding between the block and wall
The correct Answer is:a.f=√F2+m2g2+2fmgcosθ
b.F=−mgcosθ+√m2g2cos2θ−m2(g2−μ2a2)
Adopting ground frame method we have mentioned normal reaction N applied force F gravity mg and friction f (arbitearity assumed) in the FBD (fig(a and b)].
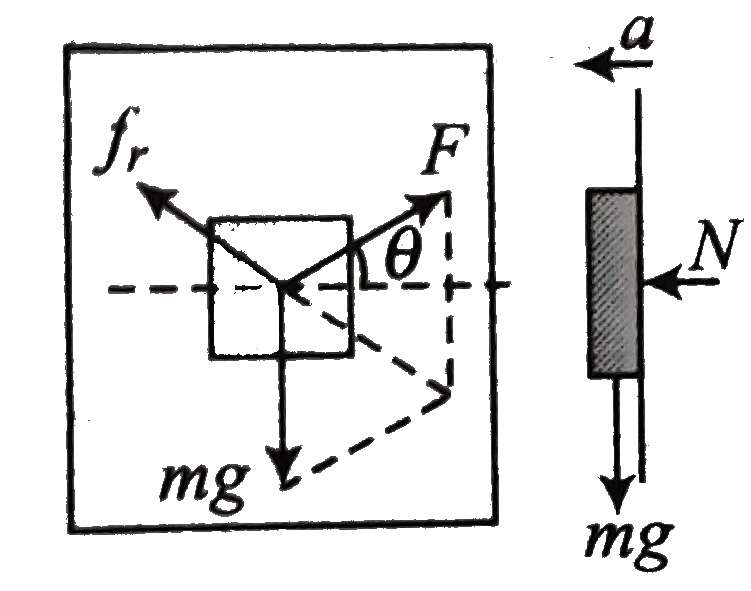
Force equation :Appling Newton 2nd law on the block , we have f+∑→F∣∣=m→a∣∣ where →a∣∣=0 because the block does not side vertically. This given →f+∑→F∣∣=0 where ∑→F∣∣=m→g+→F This yieds →f+→F+m→g=0. Hence we have →f+−(→F+m→g) as the angle between →F and m→g is θwe have
f=√F2+m2g2+2Fmgcosθ
where→F is direction opposite to the resulting of →F and m→g
b. Force equation : Appling law of motion perpendicular to the plane we have N=ma
Law of static friction : The gives as the magnitude of limiting friction fmax=μsN=μsma
where fsmax=√F2+m2g2+2Fmgcosθ
Then we have √F2+m2g2+2Fmgcosθ=μsma
F=−mgcosθ+√m2g2cos2θ−m2(g2−μ2a2)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct87videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.327videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A block of mass m is at rest under the action of force F against a wall as shown in figure. Which of the following statement is incorrect?
 View Solution
View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block
 View Solution
View SolutionA block of 50 N is pressed normally against a wall as shown. The frictional force acting on the block is :
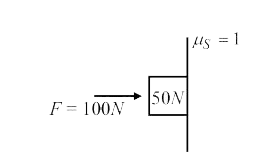 ]View Solution
]View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is pressed against a vetical wall with a horizontal force F=mg, Anogher force F=mg/2 is acting vertically upon the block. If the coefficient of friction between the block and wall is 1/2. the force of friction between them is
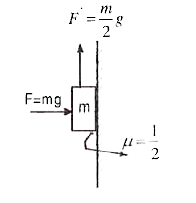 View Solution
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of mass 'M' is pressed against a wall with a horizontal force F. Then
a) it will slide down if the wall is smooth
b) frictional force may balance the weight if the wall is rough
c) Normal reaction is equal to weight of the block
d) Normal reaction is zero if the wall is smoothView Solution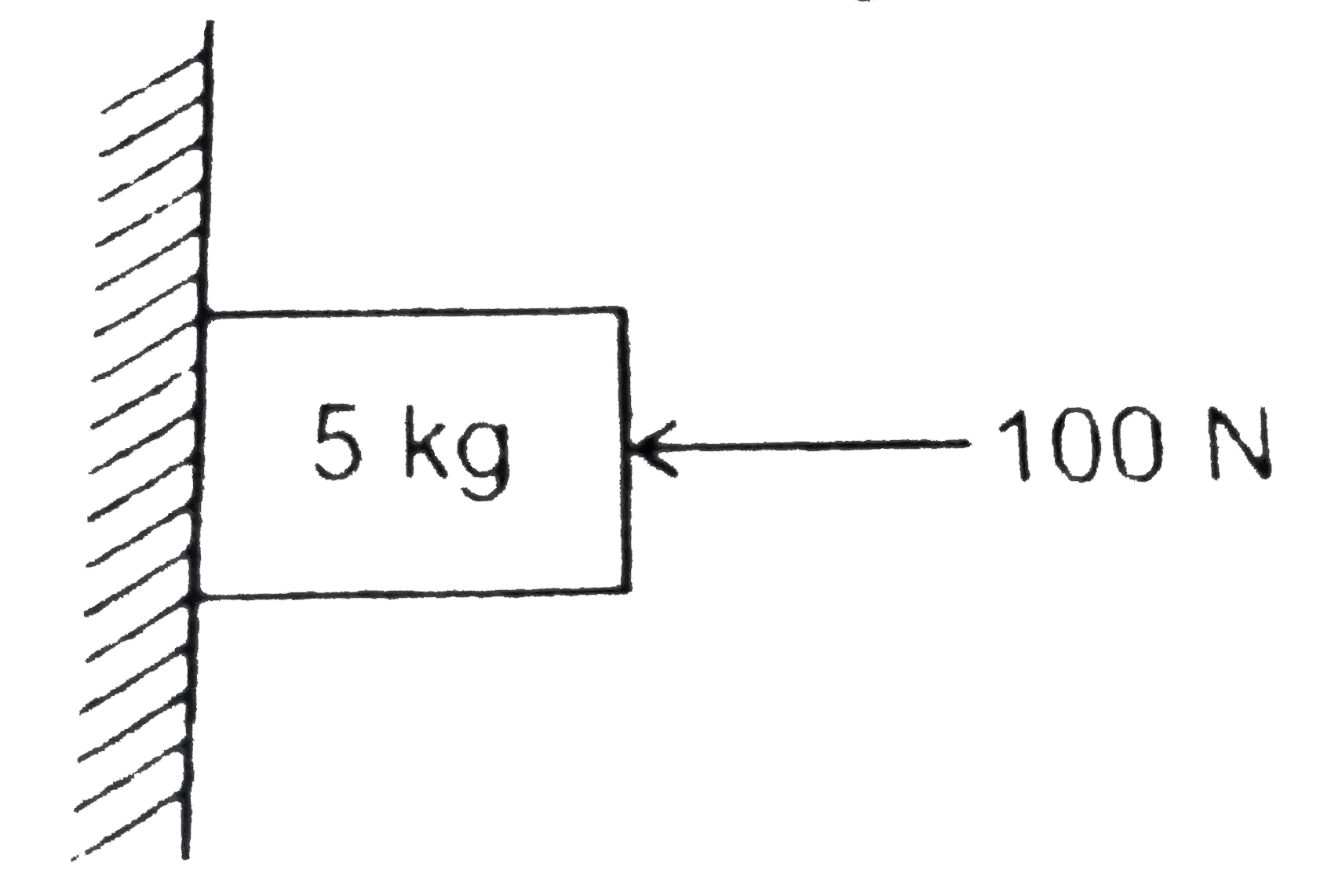
A block of mass 5 kg is held against a wall with a force of 100 N. as shown in figure. It is moved horizontally slowly by applying a force parallel to the wall. Thent he frictional force on the block due to wall is 25x newton find x. (given μ=0.5 and g=10msec2View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
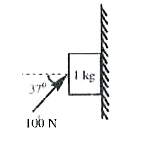 View Solution
View Solution
