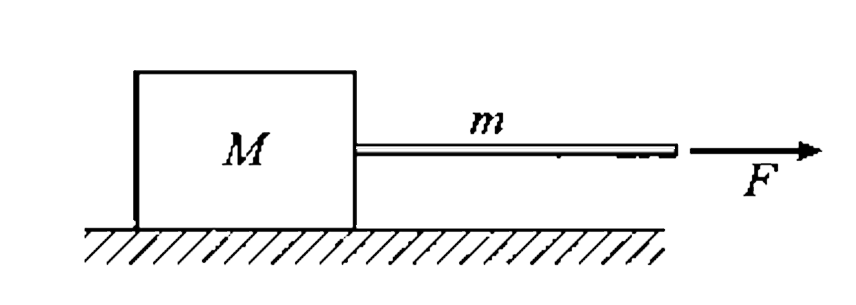
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force P is applied at one end of rope. The force which the rope exerts on the block is:
P(M−m)
PM(m+M)
PM(m+M)
PM(M−m)
The correct Answer is:C
To solve the problem of finding the force that the rope exerts on the block, we can follow these steps:
Step 1: Understand the System
We have a block of mass M and a rope of mass m on a frictionless surface. A force P is applied to one end of the rope. We need to find the force Fb that the rope exerts on the block.
Hint: Identify all the components involved, including the applied force, the masses of the block and rope, and the direction of forces.
Step 2: Set Up the Free Body Diagram
Draw a free body diagram for the rope. The forces acting on the rope are:
- The applied force P acting in the direction of the rope.
- The force Fr exerted on the rope by the block (which acts in the opposite direction).
Hint: Visualizing the forces will help you understand how they interact with each other.
Step 3: Apply Newton's Second Law to the Rope
According to Newton's second law, the net force acting on the rope is equal to the mass of the rope times its acceleration A. The equation can be written as:
P−Fr=m⋅A
Hint: Remember that the net force is the difference between the applied force and the force exerted by the block.
Step 4: Determine the Acceleration of the System
The total mass of the system (block + rope) is M+m. The acceleration A of the entire system can be expressed as:
A=PM+m
Hint: The acceleration is the same for both the block and the rope since they are connected.
Step 5: Substitute Acceleration into the Equation
Substituting A into the equation from Step 3 gives:
P−Fr=m⋅PM+m
Hint: This substitution allows us to relate the forces directly to the applied force P.
Step 6: Solve for the Force Exerted by the Rope on the Block
Rearranging the equation to solve for Fr:
Fr=P−m⋅PM+m
Factoring out P gives:
Fr=P(1−mM+m)=P(MM+m)
Hint: Factoring out common terms simplifies the expression.
Step 7: Relate Fr to Fb
According to Newton's third law, the force exerted by the rope on the block Fb is equal in magnitude to the force Fr:
Fb=Fr=M⋅PM+m
Hint: Remember that action and reaction forces are equal and opposite.
Final Answer
The force which the rope exerts on the block is:
Fb=M⋅PM+m
We have a block of mass M and a rope of mass m on a frictionless surface. A force P is applied to one end of the rope. We need to find the force Fb that the rope exerts on the block.
Draw a free body diagram for the rope. The forces acting on the rope are:
- The applied force P acting in the direction of the rope.
- The force Fr exerted on the rope by the block (which acts in the opposite direction).
According to Newton's second law, the net force acting on the rope is equal to the mass of the rope times its acceleration A. The equation can be written as:
P−Fr=m⋅A
The total mass of the system (block + rope) is M+m. The acceleration A of the entire system can be expressed as:
A=PM+m
Substituting A into the equation from Step 3 gives:
P−Fr=m⋅PM+m
Rearranging the equation to solve for Fr:
Fr=P−m⋅PM+m
Factoring out P gives:
Fr=P(1−mM+m)=P(MM+m)
According to Newton's third law, the force exerted by the rope on the block Fb is equal in magnitude to the force Fr:
Fb=Fr=M⋅PM+m
The force which the rope exerts on the block is:
Fb=M⋅PM+m
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Basic Concept Of Static And Kinetic Frictions
45 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Dynamics Of Circular Motion
31 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle
19 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force F is applied at one end of the rope. Find the force which the rope exerts on the block.
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope , the force exerted by the rope on the block .
View Solution
Knowledge Check
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force F is applied at one end of the rope, the force which the rope exerts on the block is :
AF/(M+m)BFCFM(m+M)D0A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
APm(M+m)BPm(M−m)CPDPM(M+m)A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
A(a) PmM+mB(b) PmM−mC(c) PD(d) PMM+m
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block will be
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . A force P is applied to the other end of the rope . (a) Find the acceleration of the block and the rope . (b) Find the force that the rope exerts on the block M in terms of P, M and m .
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View Solution
A block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given above. What force is exerted by the rope on the block ?
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m, as shown in figure-2.27. A horizontal force F is applied to one end of the rope. (a) Find the force the rope exerts on the blocks, and (b) the tension in the rope at its midpoint.
[MFM+m,(m+m/2)FM+m]
View Solution
