A large cubical shaped block of mass M rests on a fixed horizontal surface. Two blocks of mass m1 and m2 are connected by a light inextensible string passing over a light pulley as shown. Neglect friction everywhere. Then the constant horizontal force of magnitude F that should be applied to M so that m1 and m2 do not mov relative toM is:
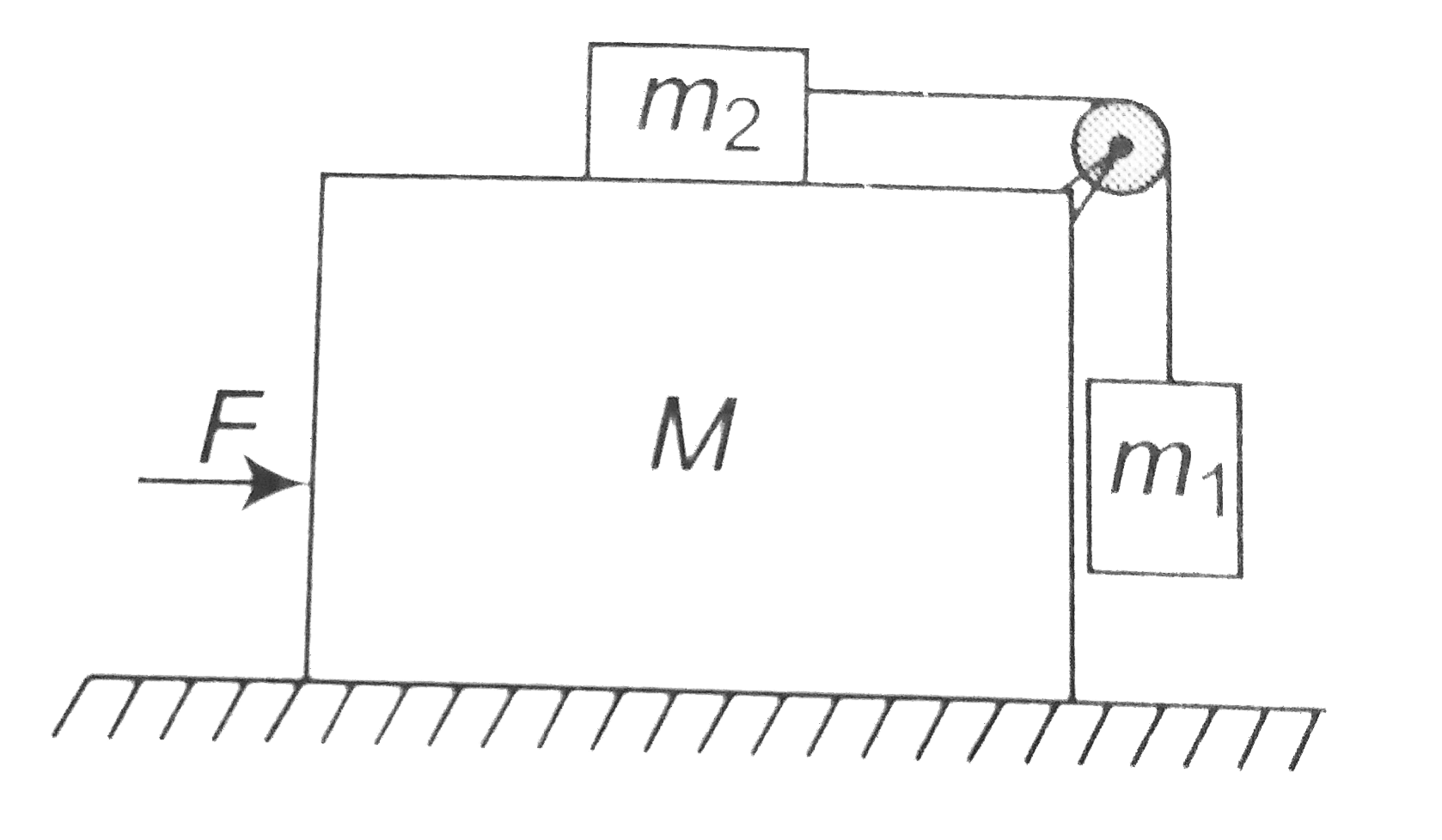
F=m2m1(m1+m2+M)g
F=m1m2(m1+m2+M)g
F=m1m2(m1+M)g
F=m2m1(m1+M)g
The correct Answer is:B
Let a be the acceleration of cubical block of mass M from gorund frame. Them from the frame of block of mass M , force on m1 and m2 are as shown. Hence for m1 and m2 to remain at rest in frame of M
m2a=m1g or a=m1m2g
:. Fm1m1(m1+m2+M)g . 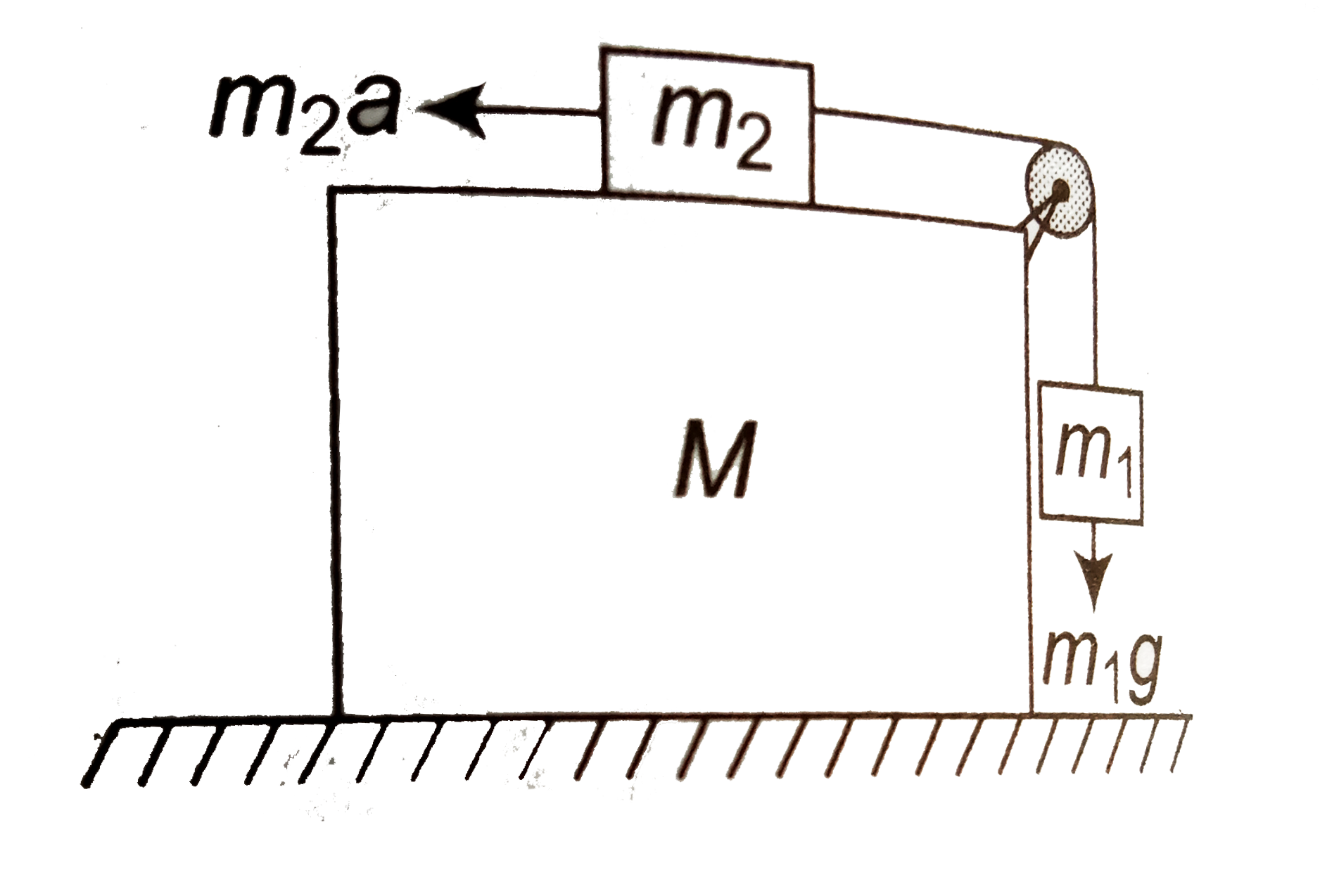
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Basic Concept Of Static And Kinetic Frictions45videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Dynamics Of Circular Motion31videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle19videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test29videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
Similar Questions
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above - Question 2 - Select One or More
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g - Question 3 - Select One or More
Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
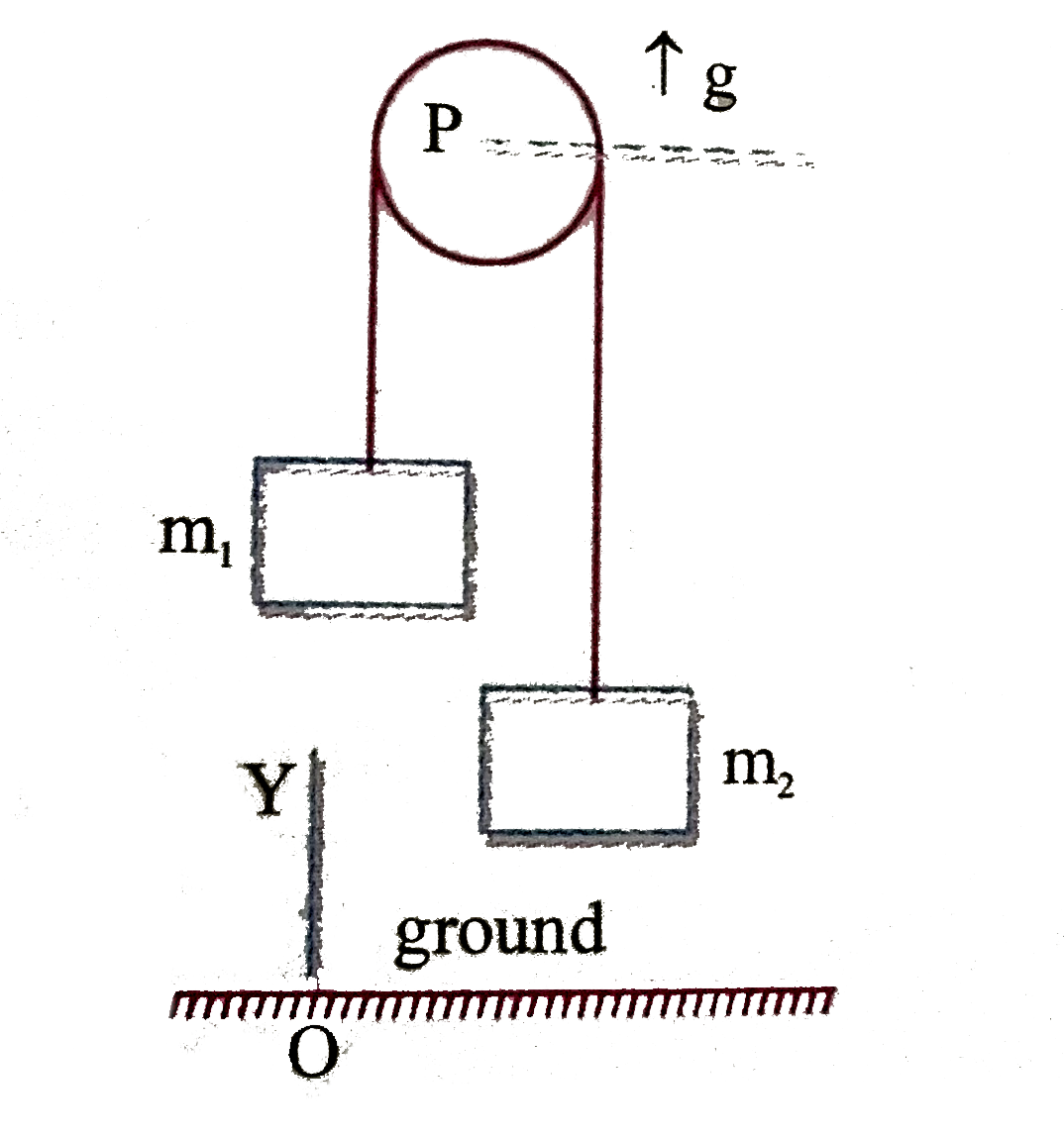 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
A block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
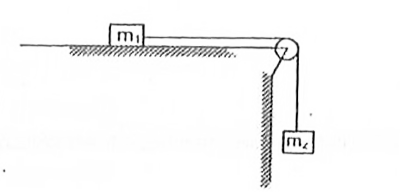 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
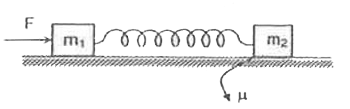 View Solution
View SolutionAll surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m1 and m2 do not move relative to m3 is :–
 View Solution
View SolutionTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
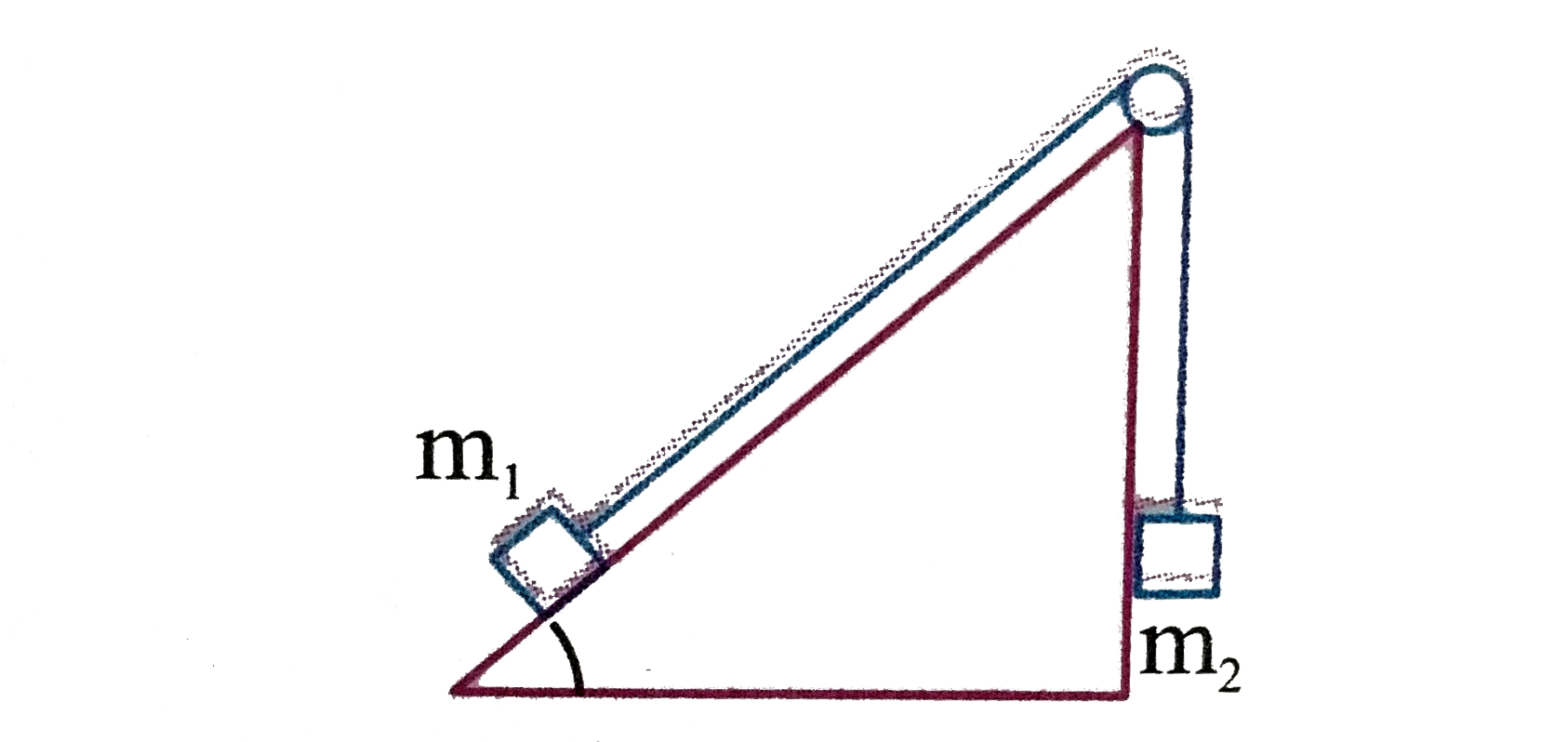 View Solution
View Solution

