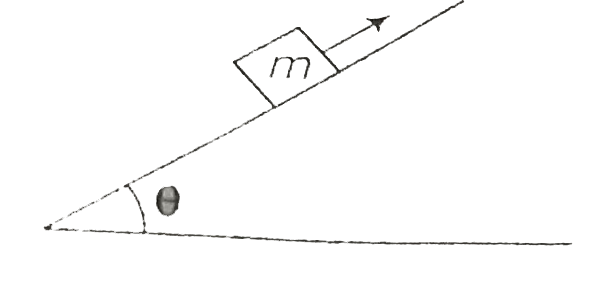
A block of mass m is thrown upwards with some initial velocity as shown in figure. On the block
Column IColumn II(A) Net force in horizontal direction(p) Zero(B) Net force in vertical direction(q)m(gsinθ+μgcosθ)(C) Net force along the plane(r)m(gsinθcosθ+μgcos2θ)(D) Net force perpendicular to plane(s)m(gsin2θ+μgsinθcosθ)
The correct Answer is:A→r,B→s,C→q,D →p
Force of friction and mgsinθ both are downwards.
∴ Acceleration of the block is a=(gsinθ+μgcosθ) down the plane
Now, net force in any direction is equal to, F=m(component of acceleration in that direction)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Assertion and reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Block of mass 'm' is sliding up on the smooth incline plane, with some constant velocity. Now, on the block match the magnitude value of the forces on 'm' in the given directions take the components of all the forces in the given direction)
Column - IColumn -IIA) Net force component is horizontal direction P) zeroB) Net - force compnent in vertical directionQ) mgsinθcosθC) Net force component along the incline plane R)mgsinθD) Net force component perpendicular to the incline plane S) mg(1−cos2θ)
View Solutioncosmθ=sinnθ then θ=
View Solution
Knowledge Check
If sinθ+cosθ=m and sinθ−cosθ=n , then
Am2+n2=1Bm2−n2=1Cm2+n2=2Dm2−n2=2If sinθ,1,cos2θ are in G.P. , then θ =
Anπ+(−1)nπ2Bnπ+(−1)n−1π2C2nπDnone8sinθ⋅cosθ⋅cos2θ⋅cos4θ= A)sin4θB)sin8θC)sin16θD)cos8θ
Asin4θBsin8θCsin16θDcos8θ
If tanθ=mn then msinθ+ncosθmsinθ−ncosθ=
View SolutionBlock of mass m is sliding up on the smooth inclined plane with some initial velocity Now on the block match the magnitude value of the forced on 'm' in the given directions (take the component of all the forces in the given direction)

Column -IColumn -II(a)Net force component inhorizontal direction(p) Zero(b)Net force component invertical direction(q)mgsinθcosθ(c)Net force componentalong the inclined plane(r)mgsinθ(d)Net force componentpenpendicular to the inclined plane(s)mg(1−cos2θ)
View Solutioncosmθ−sinnθ=0
View SolutionShow that none of the following is an identity:
(i)cos2θ+cosθ=1 (ii)sin2θ+sinθ=2 (iii)tan2θ+sinθ=cos2θ
View SolutionIf p=2sinθ1+cosθ+sinθ,andq=cosθ1+sinθ, then
View Solution
