A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is
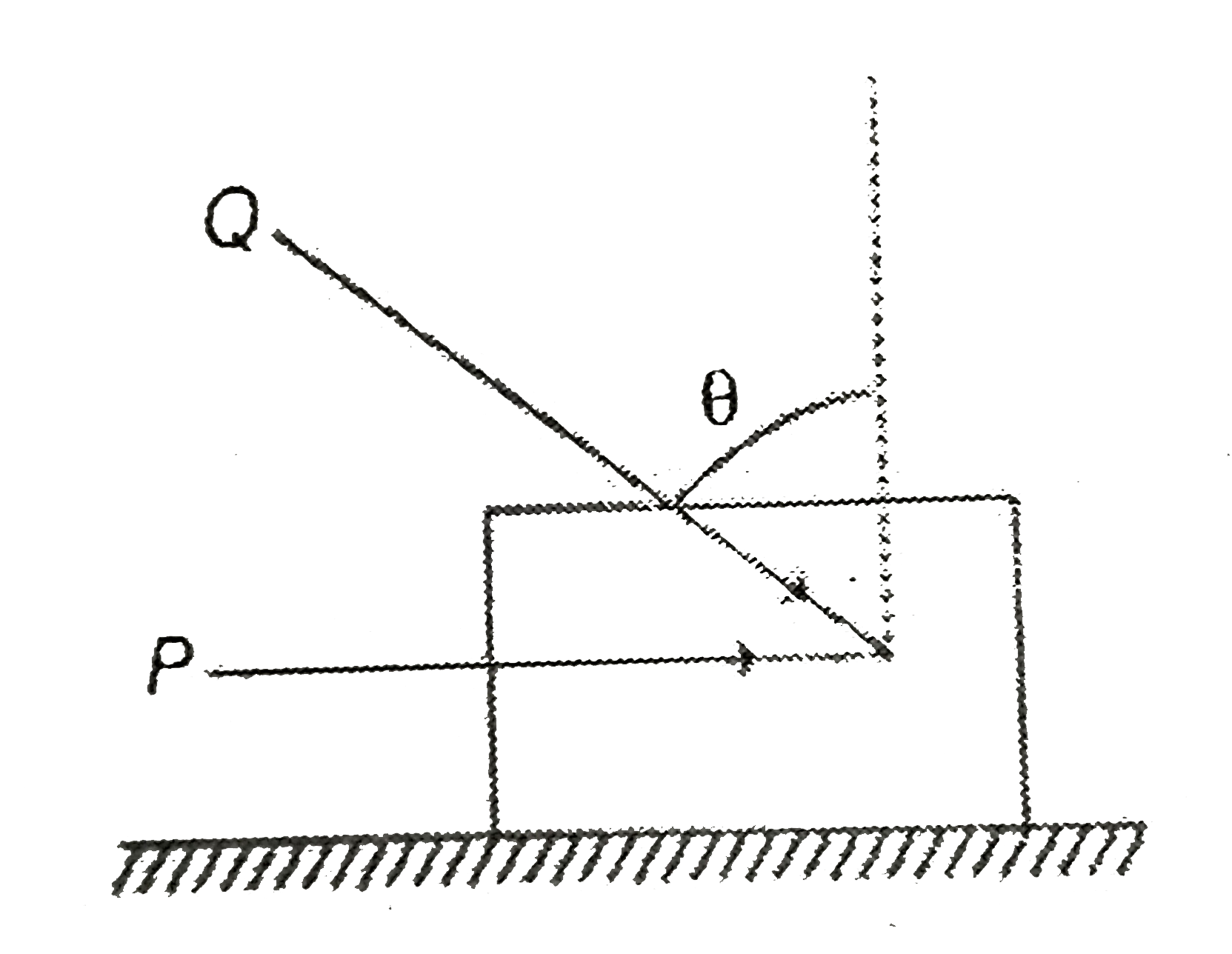
The correct Answer is:A
(a)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Assertion and reason
28 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
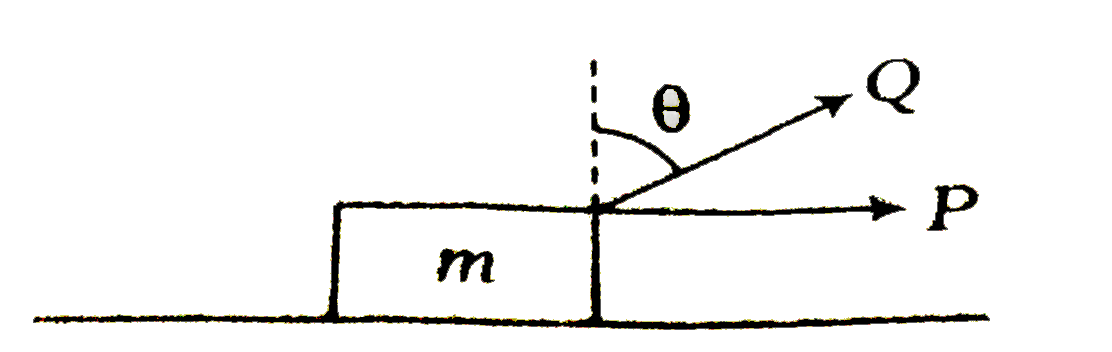
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
View SolutionA block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View Solution
Knowledge Check
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
 AP+Qsinθmg+QcosθBPcosθ+Qmg−QsinθCP+Qcosθmg+QsinθDPsinθ+Qmg−Qcosθ
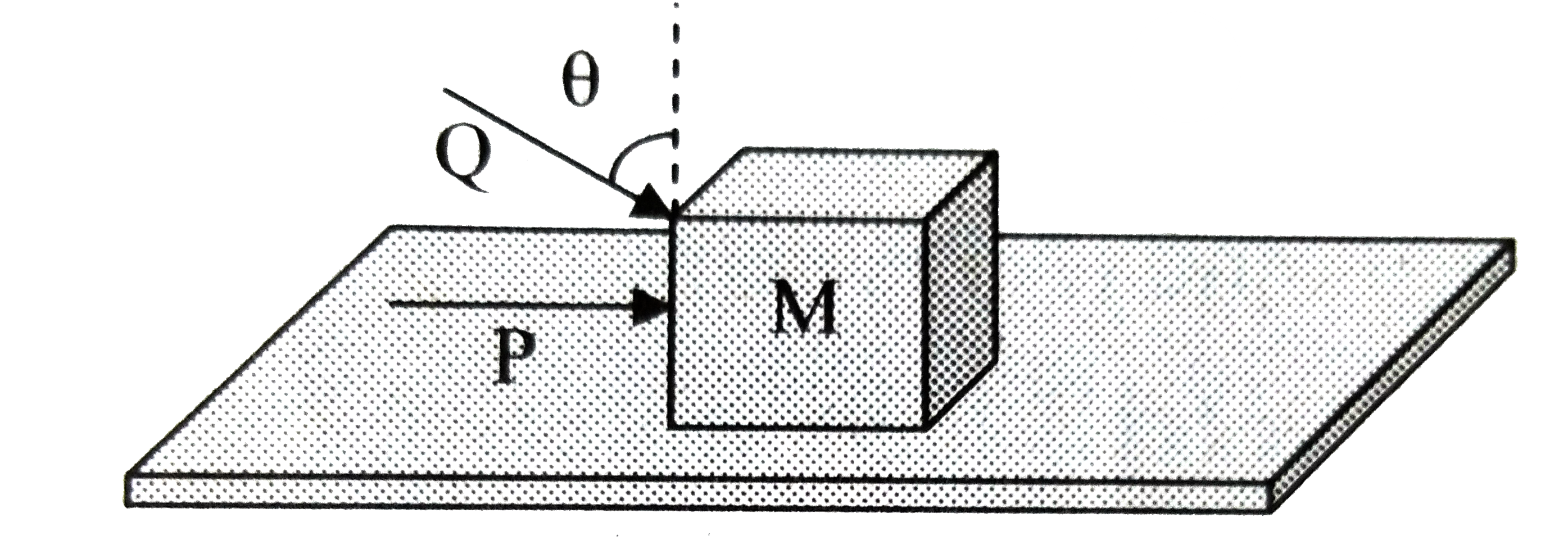
AP+Qsinθmg+QcosθBPcosθ+Qmg−QsinθCP+Qcosθmg+QsinθDPsinθ+Qmg−QcosθA block of mass m lying on a horizontal plane , is acted upon by a horizontal force p and another force Q inclined at an angle θ to the vertical .The block will remain in equilibrium if the coefficient of friction between it and the surface is (assume p>Q)
 A(Psinθ−Q)/(mg−cosθ)B(P−Qsinθ)/(mg+cosθ)C(Pcosθ+Q)/(mg−cosθ)D(P+Qsinθ)/(mg+Qcosθ)
A(Psinθ−Q)/(mg−cosθ)B(P−Qsinθ)/(mg+cosθ)C(Pcosθ+Q)/(mg−cosθ)D(P+Qsinθ)/(mg+Qcosθ)
A wedge of mass m, lying on a rough horizontal plane, is acted upon by a horizontal force F1 and another force F2, inclined at an angle θ to the vertical. The block is in equilibrium, then minimum coefficient of friction between it and te surface isA(F2sinθ)/(mg+F2cosθ)B(F1cosθ+F2)/(mg−F2sinθ)C(F1+F2sinθ)/(mg+F2cosθ)D(F2sinθ−F2)/(mg−F2cosθ)
A block of weight 200N is pulled along a rough horizontal surface at constant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is
View SolutionA block of weight 200N is pulled along a rough horizontal surface at contant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is .
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
View SolutionA block of weight w rests on a horizontal plane. A force P inclined at an angle theta to the plane is applied to the block until it is on the of motion. Find the value of coefficient of friction.
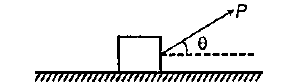
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
View Solution
