A block of mass m=0.14kg is moving with velocity v0 towards a mass less unstretched spring of force constant K=10Nm−1. Coefficient of friction between the block and the ground is μ=1/2.

Find the maximum value of compression in the spring (in cm), so that after pressing the spring the block does not return back but stops there permanently.
The correct Answer is:(7)
Let compression in the spring be x.

fl≥kξmplies(1/2)×0.14×10>10x
⇒x≤0.07m=7cm
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass 2 kg is moving on a frictionless horizontal surface with a velocity of 1m/s towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100N/m. Find the rnaximum compression of the spring
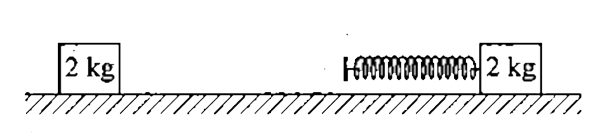
View SolutionTwo blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View Solution
Knowledge Check
A block mass m=2kg is moving with velocityv0 towards a massless unstretched spring of the force constant k=10N/m. Coefficient of friction between the block and the ground is μ=0.2. Find the maximum value of v0 so that after pressing the spring the block does not return back but stops there permanently.
 A2√25m/sB√15m/sC4√15m/sD4√25m/s
A2√25m/sB√15m/sC4√15m/sD4√25m/sA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A block of mass 0.18 kg is attached to a spring of force constant 2N/m. The coefficient of friction between the block and the floor is 0.1. Initially, the block is at rest and the spring is unstretched. An impulse is given to the block.
The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is v=N/10. Then, N is
View SolutionA block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness k=100N/m with a velocity 2m/s, the maximum compression of the spring is

View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
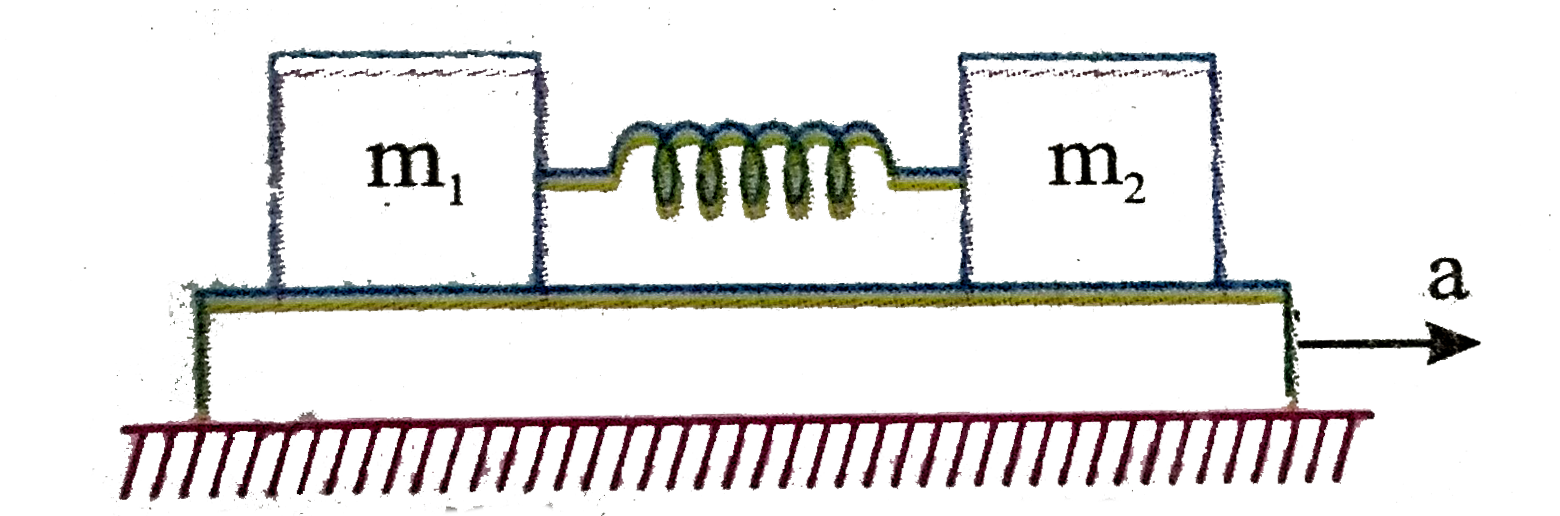
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionA block of mass 1kg moves towards a spring of force constant 10N/m. The spring is massless and unstretched. The coeffcient of friction between block and surface is 0.30. After compressing the spring, block does not return back : (g=10m/s).
View Solution
