A block of mass m1 rests on a rough horizontal plane with which its coefficient of friction is μ. A light string attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure-2.213. When the system is just about to move, find the value of μ in terms of m1m2 and α. Also find the tension in the string.
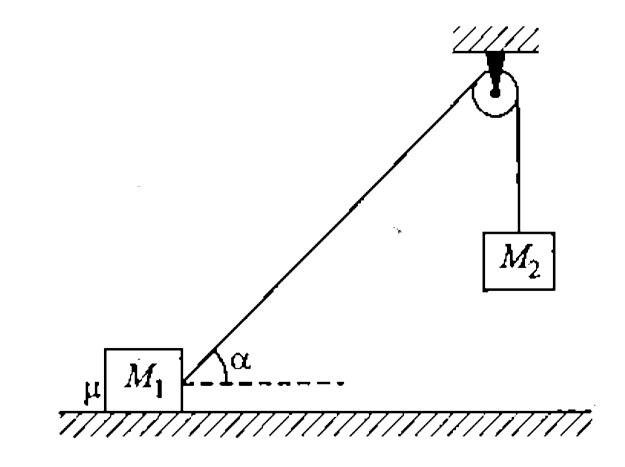
The correct Answer is:[m2cosαm1−m2sinα]
Step by step video, text & image solution for A block of mass m_(1) rests on a rough horizontal plane with which its coefficient of friction is mu. A light string attached to this block passes over a light frictionless pulley and carries another block of mass m_(2) as shown in figure-2.213. When the system is just about to move, find the value of mu in terms of m_(1) m_(2) and alpha. Also find the tension in the string. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Advance MCQs
17 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
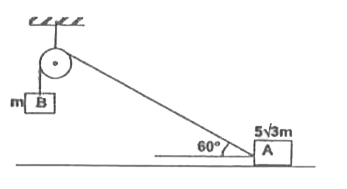
A block A of mass 5√4m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
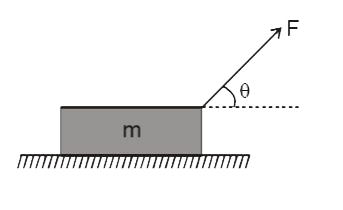
View SolutionA wooden block of mass m resting on a rough horizontal table (coefficient of friction =μ ) is pulled by a force F as shown in figure.The acceleration of the block moving horizontally is:
View Solution
Knowledge Check
A block of mass m1 rests on a rough horizontal plane with coefficient of friction as μ. A light strin attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure. If the system is just about to move, then find the value of μ.
 Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinα
Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinαA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
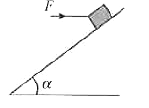 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of theseThe block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mg
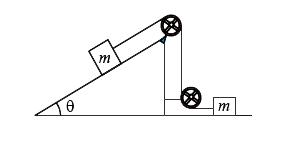
Two blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View SolutionA block of mass m1 on asmooth, horizontal surface is connected to a second mass m2 by a light string over a height, frictionless pulley. A force of magnitude F0 is applied to mass m1. Find the value of force F0 for which the system will be is equilibrium.

View SolutionA block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
View Solution
