A body completes one revolution along a horizontal circle in 10 s when tied to a cord. If the radius of the circle is decreased to one-third of its original value, then what will be the time period of revolution of the body?
The correct Answer is:(109s)
To solve the problem, we need to understand the relationship between the time period of revolution, the radius of the circle, and angular momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
The body completes one revolution in 10 seconds with an initial radius r. The time period T1 is given as:
T1=10s
Step 2: Relate Time Period to Angular Velocity
The angular velocity ω is related to the time period T by the formula:
ω=2πT
Thus, the initial angular velocity ω1 can be calculated as:
ω1=2πT1=2π10=π5rad/s
Step 3: Understand the Change in Radius
The radius of the circle is decreased to one-third of its original value:
r′=r3
Step 4: Apply Conservation of Angular Momentum
Since no external torque is acting on the system, angular momentum is conserved. The initial angular momentum Li can be expressed as:
Li=I1ω1
Where I1 is the moment of inertia at radius r.
The final angular momentum Lf when the radius is r′ is:
Lf=Ifωf
Where ωf is the final angular velocity and If is the moment of inertia at radius r′.
Step 5: Calculate Moment of Inertia
The moment of inertia I for a point mass at a distance r is given by:
I=mr2
Thus,
- Initial moment of inertia:
I1=mr2
- Final moment of inertia:
If=m(r′)2=m(r3)2=mr29
Step 6: Set Up the Conservation Equation
Using the conservation of angular momentum:
I1ω1=Ifωf
Substituting the values:
mr2⋅π5=mr29⋅ωf
Step 7: Simplify and Solve for Final Angular Velocity
Canceling m and r2 from both sides:
π5=ωf9
Rearranging gives:
ωf=9π5rad/s
Step 8: Calculate the Final Time Period
Now, we can find the new time period T2 using the relationship between angular velocity and time period:
T2=2πωf=2π9π5=2⋅59=109s
Final Answer
The time period of revolution of the body when the radius is decreased to one-third of its original value is:
T2=109s
---
The body completes one revolution in 10 seconds with an initial radius r. The time period T1 is given as:
T1=10s
The angular velocity ω is related to the time period T by the formula:
ω=2πT
Thus, the initial angular velocity ω1 can be calculated as:
ω1=2πT1=2π10=π5rad/s
The radius of the circle is decreased to one-third of its original value:
r′=r3
Since no external torque is acting on the system, angular momentum is conserved. The initial angular momentum Li can be expressed as:
Li=I1ω1
Where I1 is the moment of inertia at radius r.
Lf=Ifωf
Where ωf is the final angular velocity and If is the moment of inertia at radius r′.
The moment of inertia I for a point mass at a distance r is given by:
I=mr2
Thus,
- Initial moment of inertia:
I1=mr2
- Final moment of inertia:
If=m(r′)2=m(r3)2=mr29
Using the conservation of angular momentum:
I1ω1=Ifωf
Substituting the values:
mr2⋅π5=mr29⋅ωf
Canceling m and r2 from both sides:
π5=ωf9
Rearranging gives:
ωf=9π5rad/s
Now, we can find the new time period T2 using the relationship between angular velocity and time period:
T2=2πωf=2π9π5=2⋅59=109s
The time period of revolution of the body when the radius is decreased to one-third of its original value is:
T2=109s
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions24videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS TOUGH & TRICKY8videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)16videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A ball tied to a string takes us to complete revolution along a horizontal circle. If, by pulling the cord, the radius of the circle is reduceed to half of the previous value, then how much time the ball will take in one revolution?
View SolutionA ball tied to a string takes 4s to complete one revoluting along a horizontal circule. If by pulling the cord, the radius of the circle is reduced to half, how much time will the ball take to complete one revolution ?
View Solution
Knowledge Check
- Question 1 - Select One
If the radius of a circle is decreased to 25% of its original value, calculate the percentage decrease in the area of the circle.
A25%B43.75%C50%D93.75% - Question 2 - Select One
If a body completes one revolution in π sec then the moment of inertia would be
AEqual to rotational kinetic energyBDouble of rotational kinetic energyCHalf of rotational kinetic energyDFour times the rotational kinetic energy - Question 3 - Select One
A satellite moves in a circle around the earth. The radius of this circle is equal to one half of the radius of the moon's orbit. The satellite completes one revolution is :
A1/2 lunar monthB2/3 lunar monthC2−3/2 lunar monthD23/2 lunar month
A body of mass 0.6 mg kg is whirled in a vertical circle making 5 revolutions in one second . If the radius of the circle is 1.4 m , find the tension in the string , when the body is (i) at the lower most of the circle point , (ii) at the top of the circle .
View SolutionA body completes one round of a circle of radius R in 20 second. The displacement of the body after 45 seconds is
View SolutionA body is projected from earth's surface to become its satellite, its time period of revolution will not depend upon
View SolutionIf a particle complete one and half revolution along the circumference of a circle then its angular displacement is -
View SolutionA partical revolves in clockwise direction (as seen from point A) in a circle C of radius 1 cm and completes one revolution in 2 sec. The axis of the circle and the principal axis of the mirror M coincides, call it AB. The radius of curvature of the mirror of 20cm. Then, the direction of revolution (as seen from A) of the image of the partical and its speed is
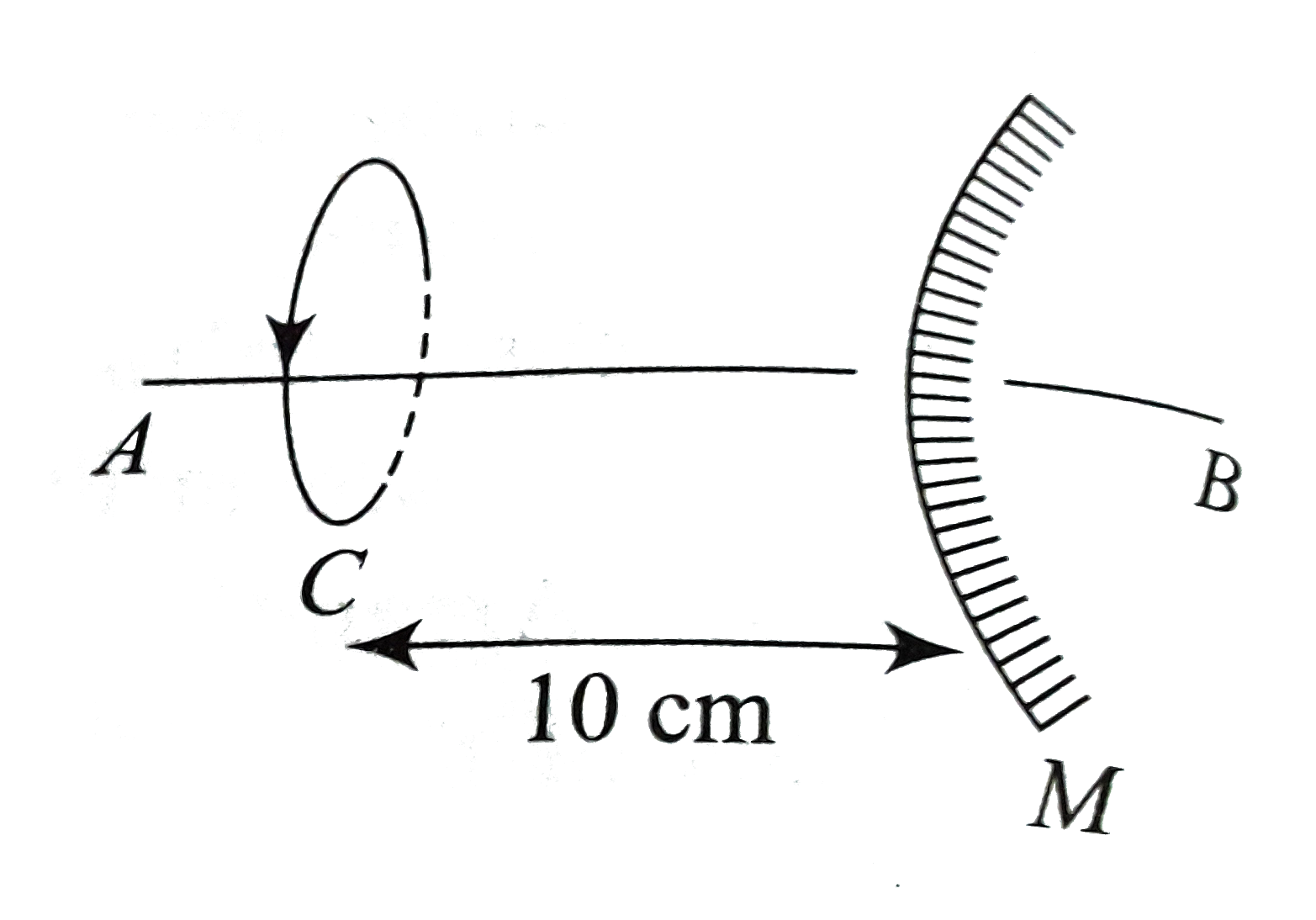 View Solution
View Solution

