A body is at rest at $x = 0$ . At $t = 0$ , it starts moving in the positive $x - d i r e c t i o n$ with a constant acceleration . At the same instant another body passes through $x = 0$ moving in the positive $x - d i r e c t i o n$ with a constant speed . The position of the first body is given by $x_{1} (t)$ after time 't', and that of the second body by $x_{2} (t)$ after the same time interval . which of the following graphs correctly describes $(x_{1} - x_{2})$ as a function of time 't' ?

A

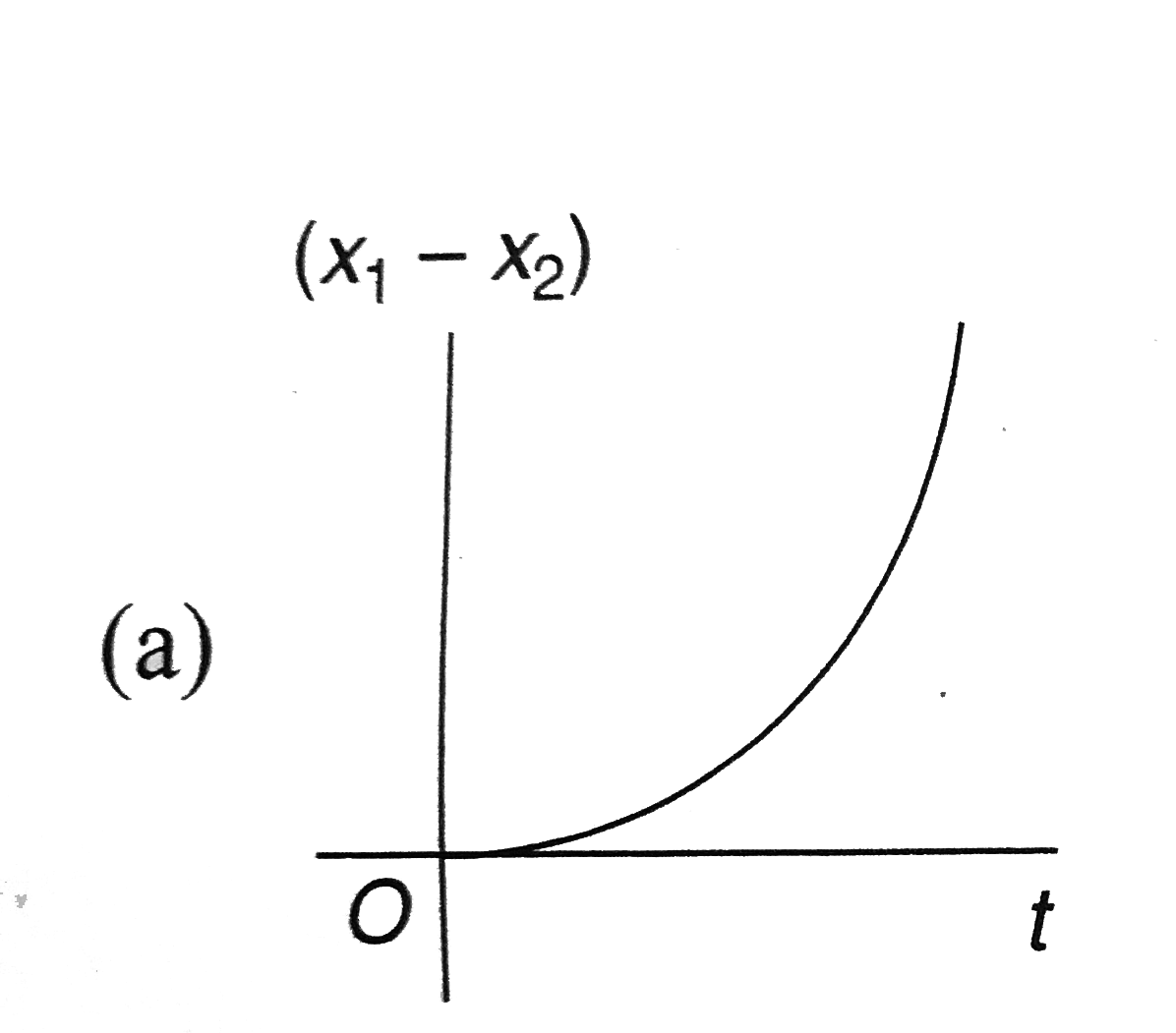
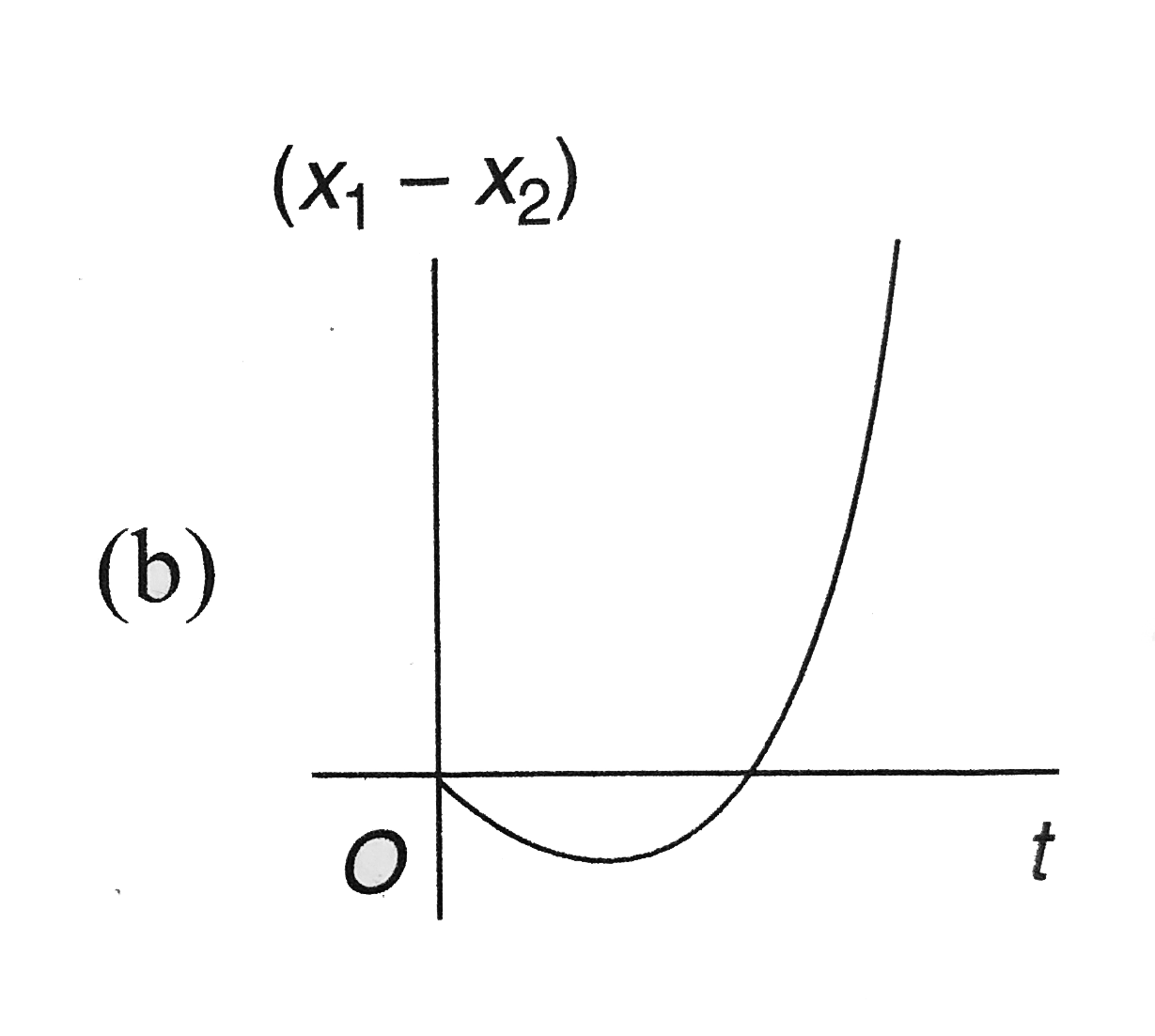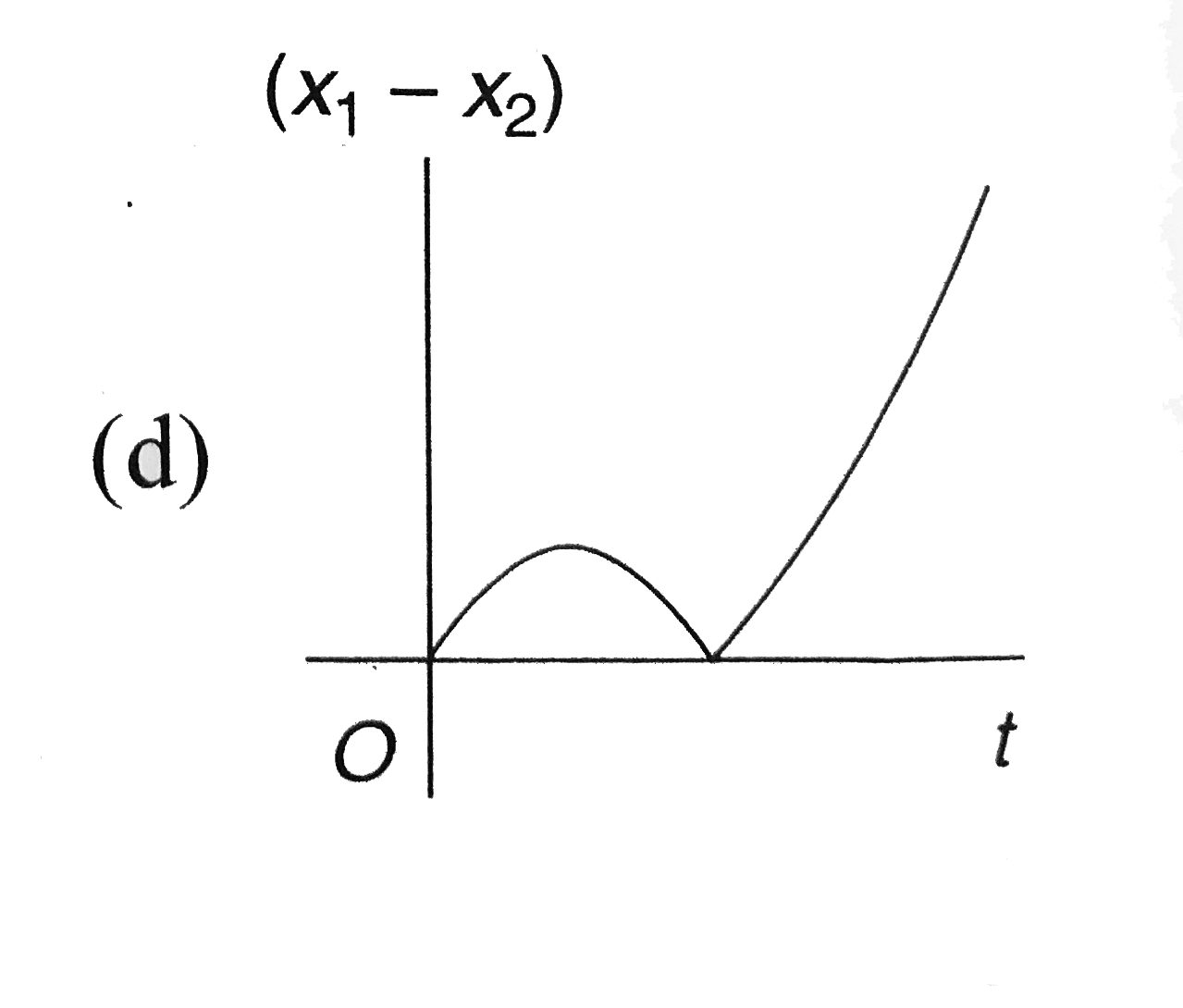ocr_image

B

ocr_image .

C

ocr_image .

D

ocr_image .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

For $1^{s t}$ particle :
It starts moving $(u_{1} = 0)$ with constant acceleration
$x_{1} = x_{1} (t) = u_{1} t + \frac{1}{2} a t^{2} = \frac{1}{2} a t^{2}$ …(i)
For $2^{n d}$ particle :
It is moving with constant velocity (v)
$x_{2} = x_{2} (t) = v t$ …(ii)
Relation position of particle '1' w.r.t. '2'
Hence $x_{1} - x_{2} = x_{1, 2} = \frac{1}{2} a t^{2} - v t$ ...(iii)
Hence graph should be parabola.
differentiating equation (iii) w.r.t time, we get the relative velocity of particle $1$ w.r.t. $2$
or $| v_{1, 2} | = \frac{{d x}_{1, 2}}{d t} = a t - v$
As particle '1' starts moving from rest, hence at $t = 0$
$v_{1, 2}$ should be negative.
It means the slope of the parabola at $t = 0$ should be negative. The parabola should open up. Hence graph 'b' fulfil the requirement.

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as $v = p \sqrt{x}$ . The displacement of the particle varies with time as (where, p is constant)
A $t^{3}$
B $t^{2}$
C $t$
D $t^{1 / 2}$
Question 2 - Select One
A particle located at $x = 0$ at time $t = 0$ , starts moving along with the positive $x - d i r e c t i o n$ with a velocity 'v' that varies as $v = a \sqrt{x}$ . The displacement of the particle varies with time as
A $t^{2}$
B $t$
C $t^{\frac{1}{2}}$
D $t^{3}$
Question 3 - Select One
A wave propagates in a string in the positive x-direction with velocity v. The shape of the string at $t = t_{0}$ is given by
$f (x, t_{0}) = A sin (\frac{x^{2}}{a^{2}})$ . Then the wave equation at any instant t is given by
A $g (x, t) = A sin \frac{{[x - v (t - t_{0})]}^{2}}{a^{2}}$
B $g (x, t) = A sin \frac{{[x + v (t - t_{0})]}^{2}}{a^{2}}$
C $g (x, t) = A sin \frac{{[x - v (t + t_{0})]}^{2}}{a^{2}}$
D $g (x, t) = A sin \frac{{[x + v (t + t_{0})]}^{2}}{a^{2}}$

A2Z-GENERAL KINEMATICS AND MOTION IN ONE DIMENSION-Problem Based On Mixed Concepts

Home
Ask Doubt
Profile