A body is performing SHM, then its
average total enregy per cycle is equal to its maximum kinetic energy
average kinetic energy per cycle is equal to half of its maximum kinetic energy
mean velocity over a complete cycle is equal to 2π times of maximum velocity
root mean square velocity is 1√2 times of its maximum velocity
To solve the question regarding a body performing Simple Harmonic Motion (SHM), we need to analyze the given options step by step.
Step 1: Understanding Total Energy in SHM
In SHM, the total mechanical energy (E) of the system is constant and is the sum of kinetic energy (KE) and potential energy (PE). The total energy can be expressed as:
E=KE+PE
For a mass-spring system, the total energy can be represented as:
E=12kA2
where k is the spring constant and A is the amplitude.
Step 2: Kinetic Energy in SHM
The kinetic energy at any point in SHM is given by:
KE=12mv2
where v is the velocity of the mass. The maximum kinetic energy occurs when the mass passes through the equilibrium position, given by:
KEmax=12m(Aω)2
where ω is the angular frequency.
Step 3: Average Kinetic Energy
The average kinetic energy over one complete cycle can be calculated. Since the average value of cos2(ωt) over one cycle is 12, the average kinetic energy is:
KEavg=12m(Aω√2)2=14mA2ω2
This shows that:
KEavg=12KEmax
Step 4: Mean Velocity in SHM
The mean velocity over one complete cycle is zero because the particle returns to its starting position. Therefore, the mean velocity is:
Vmean=0+02=0
Step 5: Root Mean Square Velocity
The root mean square (RMS) velocity can be calculated as follows:
Vrms=√1T∫T0v2dt
For SHM, this can be shown to be:
Vrms=Aω√2
This indicates that:
Vrms=1√2Vmax
Conclusion
Now, let's summarize the correctness of the options based on our findings:
1. Average total energy per cycle is equal to maximum kinetic energy: False (Total energy is constant, but not equal to max KE).
2. Average kinetic energy per cycle is equal to half of its maximum kinetic energy: True.
3. Mean velocity of a complete cycle is equal to 2π times of maximum velocity: False (Mean velocity is zero).
4. Root mean square velocity is 1√2 times of its maximum velocity: True.
Thus, the correct options are 2 and 4.
In SHM, the total mechanical energy (E) of the system is constant and is the sum of kinetic energy (KE) and potential energy (PE). The total energy can be expressed as:
E=KE+PE
E=12kA2
where k is the spring constant and A is the amplitude.
The kinetic energy at any point in SHM is given by:
KE=12mv2
where v is the velocity of the mass. The maximum kinetic energy occurs when the mass passes through the equilibrium position, given by:
KEmax=12m(Aω)2
where ω is the angular frequency.
The average kinetic energy over one complete cycle can be calculated. Since the average value of cos2(ωt) over one cycle is 12, the average kinetic energy is:
KEavg=12m(Aω√2)2=14mA2ω2
This shows that:
KEavg=12KEmax
The mean velocity over one complete cycle is zero because the particle returns to its starting position. Therefore, the mean velocity is:
Vmean=0+02=0
The root mean square (RMS) velocity can be calculated as follows:
Vrms=√1T∫T0v2dt
For SHM, this can be shown to be:
Vrms=Aω√2
This indicates that:
Vrms=1√2Vmax
Now, let's summarize the correctness of the options based on our findings:
1. Average total energy per cycle is equal to maximum kinetic energy: False (Total energy is constant, but not equal to max KE).
2. Average kinetic energy per cycle is equal to half of its maximum kinetic energy: True.
3. Mean velocity of a complete cycle is equal to 2π times of maximum velocity: False (Mean velocity is zero).
4. Root mean square velocity is 1√2 times of its maximum velocity: True.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Very Short Answer Type Qns14videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - Long answer type questions12videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A body is performing SHM At a displacement X1, its potential energy is 4 J and at a displacement X2, its potential energy is 9 J. The potential energy at a displacement (X1+X2) is
View SolutionTwo bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is
_E01_002_Q01.png) View Solution
View SolutionA body is executing S.H.M. when its displacement from the mean position is 4 cm and 5 cm, the corresponding velocity of the body is 10 cm/sec and 8 cm/sec. Then the time period of the body is
View SolutionA body is performing simple harmonic motion with amplitude a and time period T variation of its acceleration (f) with time(t) is shown in figure If at time t velocity of the body is v which of the following graph is correct?
 View Solution
View SolutionA body is performing simple harmonic motion with amplitude a and time period T variation of its acceleration (f) with time(t) is shown in figure If at time t velocity of the body is v which of the following graph is correct?
 View Solution
View SolutionA body is performing simple harmonic motion of amplitude A and time period T. The figure shown position-time graph of the body . At any time t, acceleration of the body is f, then which of the following graphs is/are appropriate?
 View Solution
View SolutionA body performs S.H.M. Its kinetic energy K varies with time t as indicated by graph
View SolutionA particle is performing SHM about mean position O as shown in the figure given below. Its amplitude is 5 m and time period of oscillation is 4 s. The minimum time taken by the particle to move from point A to B is nearly
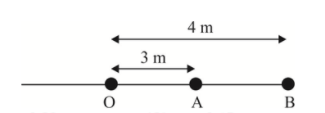 View Solution
View SolutionTwo particles are performing SHM in same phase. It means that
View SolutionA particle is performing S.H.M. Its total energy ie E When the displacement of the particle is half of its amplitude, its K.E. will be
View Solution

