A body is thrown on a rough surface such that the friction force acting on it is linearly varying with the distance travelled by it as f=ax+b. Find the work done by the friction on the box if before coming to rest the box travels a distance s.
To solve the problem of finding the work done by the friction on a box that is thrown on a rough surface, where the friction force varies linearly with distance, we can follow these steps:
Step 1: Understand the Given Information
We are given that the friction force f acting on the box is defined by the equation:
f=ax+b
where a and b are constants, and x is the distance traveled by the box. The box travels a distance s before coming to rest.
Step 2: Set Up the Work Done Formula
The work done W by a force is given by the integral of the force over the distance traveled. Since the friction force acts in the opposite direction to the motion of the box, the work done by friction will be negative:
W=−∫s0fdx
Step 3: Substitute the Expression for Friction Force
Substituting the expression for f into the work done formula, we have:
W=−∫s0(ax+b)dx
Step 4: Evaluate the Integral
Now we can evaluate the integral:
W=−(∫s0axdx+∫s0bdx)
Calculating each integral separately:
1. For the first integral:
∫s0axdx=a(x22)s0=as22
2. For the second integral:
∫s0bdx=b(x)s0=bs
Combining these results, we have:
W=−(as22+bs)
Step 5: Write the Final Expression for Work Done
Thus, the work done by the friction on the box is:
W=−12as2−bs
Summary of the Solution
The work done by the friction force on the box as it travels a distance s before coming to rest is:
W=−12as2−bs
We are given that the friction force f acting on the box is defined by the equation:
f=ax+b
where a and b are constants, and x is the distance traveled by the box. The box travels a distance s before coming to rest.
The work done W by a force is given by the integral of the force over the distance traveled. Since the friction force acts in the opposite direction to the motion of the box, the work done by friction will be negative:
W=−∫s0fdx
Substituting the expression for f into the work done formula, we have:
W=−∫s0(ax+b)dx
Now we can evaluate the integral:
W=−(∫s0axdx+∫s0bdx)
Calculating each integral separately:
1. For the first integral:
∫s0axdx=a(x22)s0=as22
2. For the second integral:
∫s0bdx=b(x)s0=bs
W=−(as22+bs)
Thus, the work done by the friction on the box is:
W=−12as2−bs
The work done by the friction force on the box as it travels a distance s before coming to rest is:
W=−12as2−bs
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA block of mass m is kept over another block of mass M nd the system rests on a horizontal force F acting on the lower block produces an accelertion F2(m+M) in the system the two blocks always move together. A. Find the coefficient of kinetic frictioin between the bigger block and th horizontal surface. b. find the frictional force acting on the smaller block. c. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
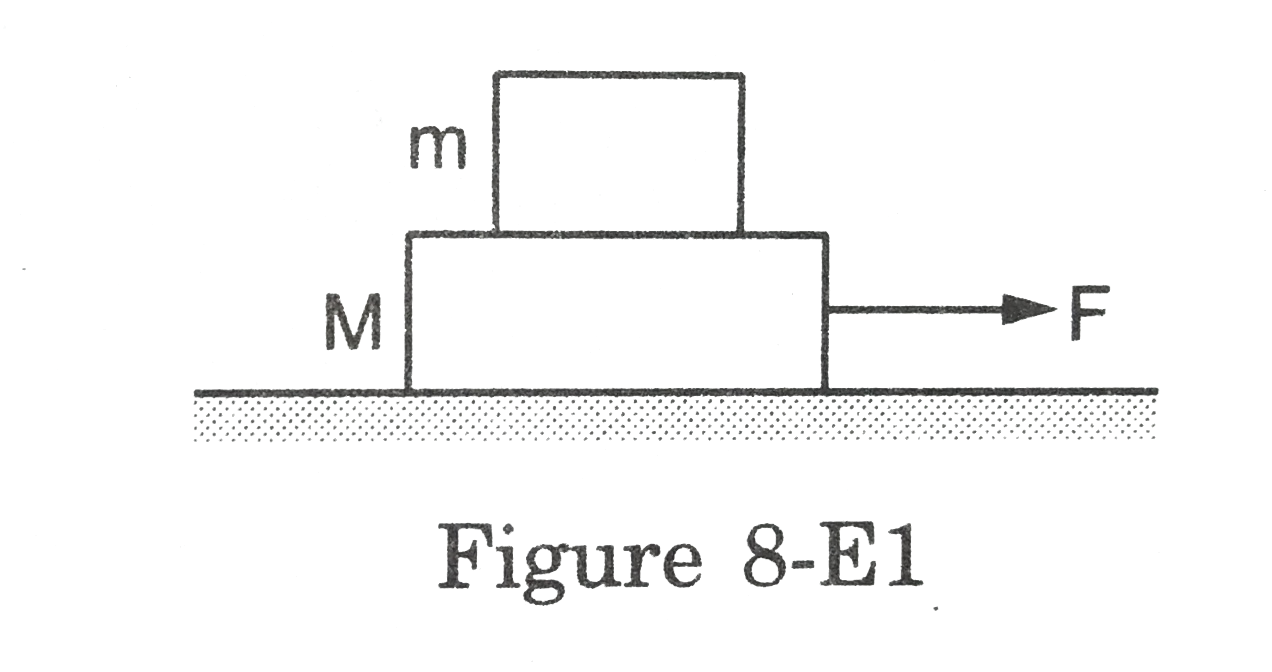
View Solution
Knowledge Check
A force F acting on an object varies with distance x as shown in the figure. The work done by the force in moving the object from x=0 to x = 20 m is
 A500 JB1000 JC1500 JD2000 J
A500 JB1000 JC1500 JD2000 JA force F acting on an object varies with distance x
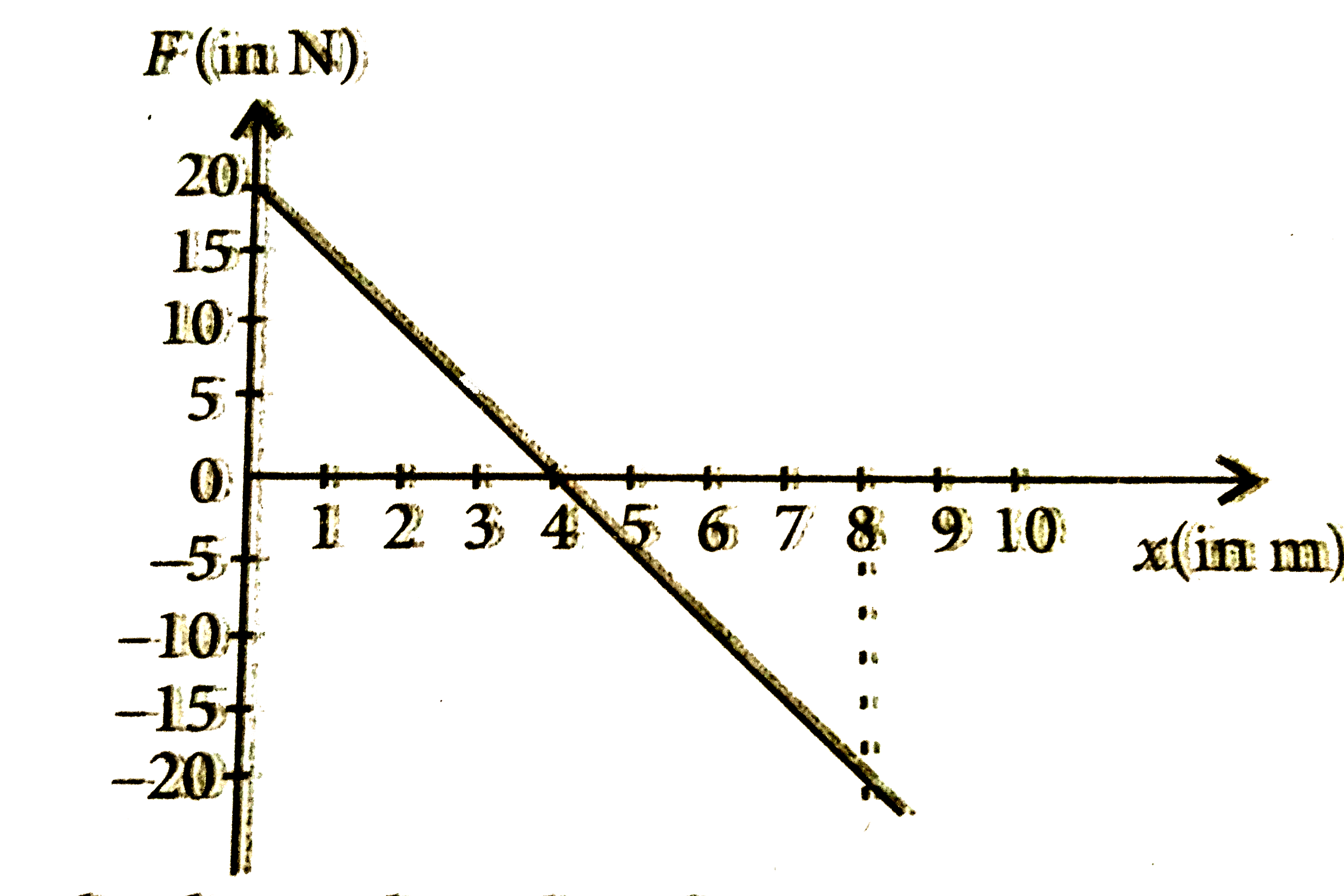
The work done by the force in moving the object from x=0 to x=8 m isAzeroB80 JC−40JD40J
Find the distance travelled by a body in 5 minutes if it travels with a uniform speed of 20 m s−1 .
View SolutionA body starts from rest, what is the ratio of the distance travelled by the body during the 4th and 3rd s?
View SolutionA block of mass m is kept over another block of mass M and the system rests on a horizontal surface. A constant horizontal force F acting on the lower block produces an acceleration F2(m+M) in the sytem. The two blocks always move together. Consider displacement d of the system.
a. Find the work done by friction on bigger block.
b. Find the coefficient of kinetic friction between the bigger block and the horizontal surface.
c. Find the frictional acting on the smaller block.
d. Find the work done by the force of friction on the smaller block by the bigger block.
e. Find the work done by static friction on bigger block.
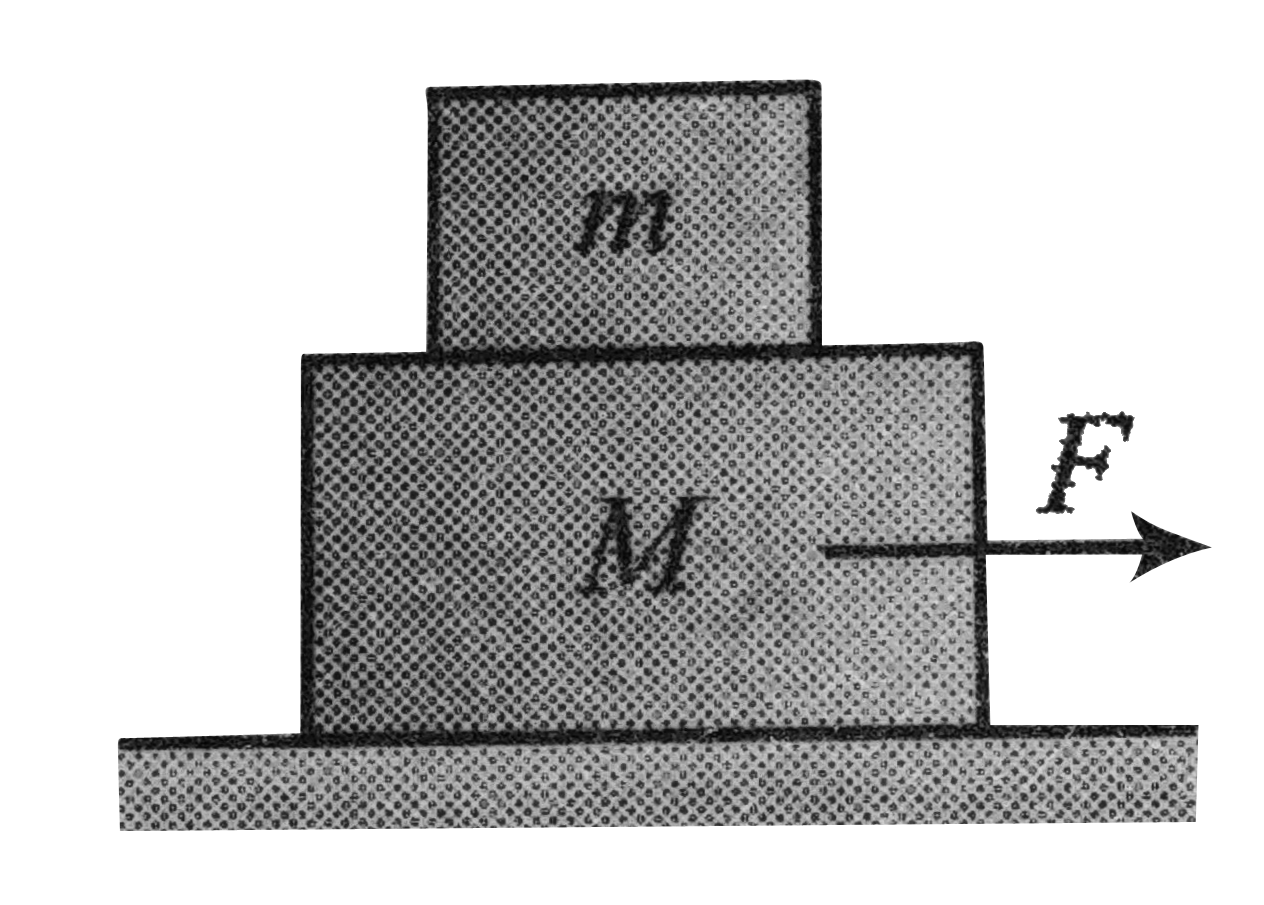
View SolutionWhen a body is rolling without slipping on a rough horizontal surface, the work done by friction is :
View SolutionA body of mass m is kept on a rough horizontal surface of friction coefficient μ . A force P is applied horizontally , but the body is not moving .Find the net force F exerted by the surface on the body .
View SolutionA body starting from rest has an acceleration of 5m/s2. Calculate the distance travelled by it in 4th second.
View Solution
