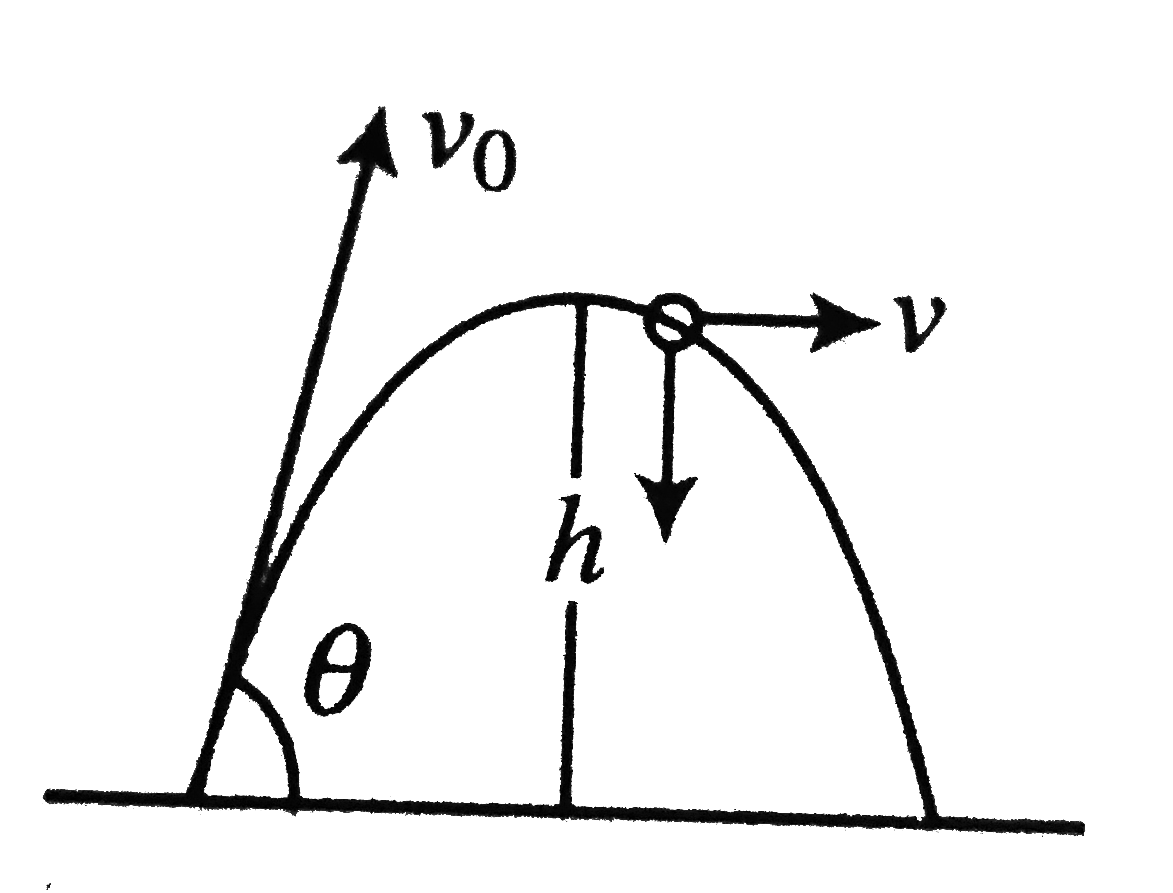
A body is thrown with the velocity at an angle of to the horizon. Determine if the maximum height attained by the body is and at the highest point of its trajectory the radius of curvature is . Neglect air resistance. .
The correct Answer is:
Radius of curvature at the highest point
…(i)
Maximum height, …(ii)
By using Eqs (i) and (ii), we get
.
Topper's Solved these Questions
Similar Questions
A particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View Solution
Knowledge Check
If a body is thrown up with the velocity of 15 m/s then maximum height attained by the body is (g=10m/s)
A11.25mB16.2mC24.5mD7.62mA body is thrown with a velocity of 9.8m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A1.5sB1sC3sD2sA particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
A25 mB30 mC35 mD40 m
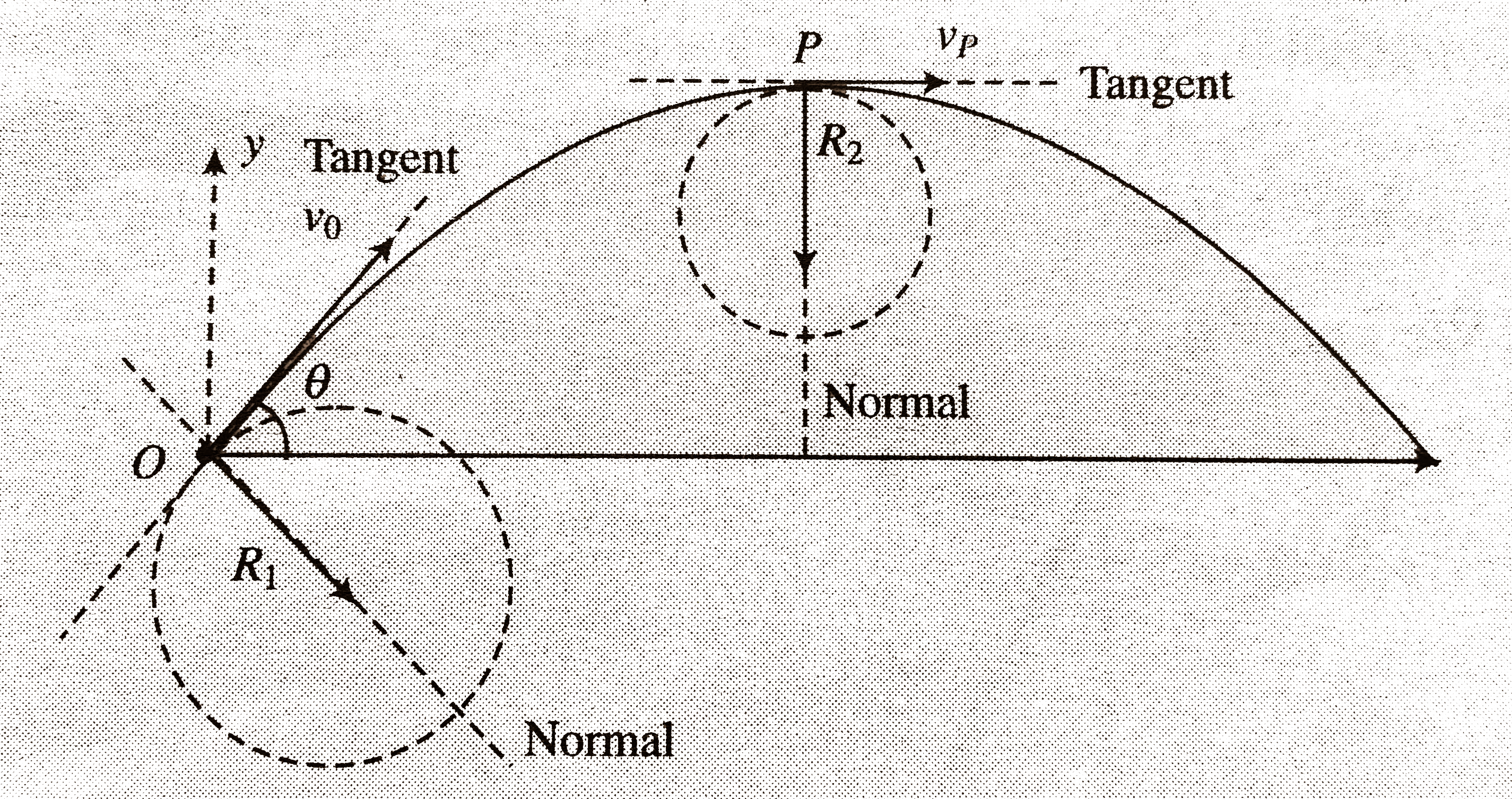
A particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
 .
.
View SolutionA particle of mass m is thrown with speed v0 at angle 30∘ with horizontal. Find the angular momentum about the point of projection when the particle is at the highest point of its trajectory.
View SolutionA body is thrown up with a velocity of 20 m/s. The maximum height attained by it is approximately
View SolutionA projectile os shot in air with velocity (v) at an angle θ with the horizontal. Neglecting the air resistance, what are the vertical acceleration and horizontal acceleration at the highest of its fligh ?
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View Solution
