A body of length 1m having cross sectional area 0.75m2 has heat flow through it at the rate of 6000Joule/sec. Then find the temperature difference if K=200Jm−1K−1.
20∘C
40∘C
80∘C
100∘C
The correct Answer is:B
To solve the problem, we will use the formula for heat conduction, which is given by Fourier's law:
dqdt=k⋅A⋅ΔTL
Where:
- dqdt is the rate of heat flow (in Joules per second),
- k is the thermal conductivity (in J⋅m−1⋅K−1),
- A is the cross-sectional area (in m2),
- ΔT is the temperature difference (in Kelvin or Celsius),
- L is the length of the body (in meters).
Given:
- dqdt=6000J/s
- k=200J⋅m−1⋅K−1
- A=0.75m2
- L=1m
We need to find the temperature difference ΔT.
Step 1: Rearranging the formula
We can rearrange the formula to solve for ΔT:
ΔT=dqdt⋅Lk⋅A
Step 2: Substituting the values
Now, we substitute the known values into the equation:
ΔT=6000J/s⋅1m200J⋅m−1⋅K−1⋅0.75m2
Step 3: Calculating the denominator
Calculating the denominator:
200⋅0.75=150J⋅K−1
Step 4: Completing the calculation
Now substituting back into the equation:
ΔT=6000150
Calculating this gives:
ΔT=40K
Conclusion
The temperature difference ΔT is 40K or 40°C.
- dqdt is the rate of heat flow (in Joules per second),
- k is the thermal conductivity (in J⋅m−1⋅K−1),
- A is the cross-sectional area (in m2),
- ΔT is the temperature difference (in Kelvin or Celsius),
- L is the length of the body (in meters).
- dqdt=6000J/s
- k=200J⋅m−1⋅K−1
- A=0.75m2
- L=1m
We can rearrange the formula to solve for ΔT:
Now, we substitute the known values into the equation:
Calculating the denominator:
Now substituting back into the equation:
The temperature difference ΔT is 40K or 40°C.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - AIIMS Questions
28 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion Reasoning
21 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test
28 Videos
Similar Questions
A rod of length1m having cross sections area 0.75m^(2), conducts heat at 6000J/sec.Then the temperature difference across the rod isK=200Wm^(-1)k^(-1)
View SolutionHeat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View Solution
Knowledge Check
The figure show a cross-section of a double glass unit of a window on a vertical wall. A graph wall. A graph of the temperature at different points within the unit is show next to it. The temperature difference across the unit is 13K. It has a crossp-sectional area of 1.3m2 and the rate of heat flow through it is 65W. Then the correct statement is (Glass has a thermal conductivity of 1Wm−1K−1)
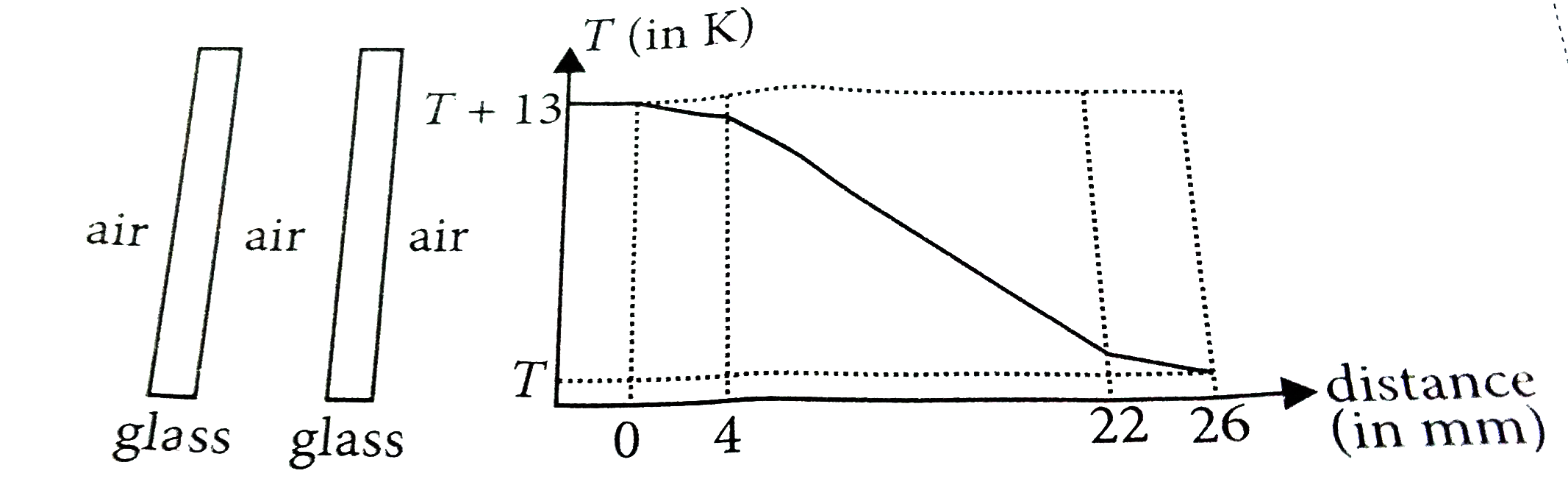 AThe unit is in steady state and in thermal equilibriumBThe unit is in steady state but not in thermal equalibrium.CThe unit is not in steady state but is in thermalDThe unit neither in steady state nor in thermal equilibrium
AThe unit is in steady state and in thermal equilibriumBThe unit is in steady state but not in thermal equalibrium.CThe unit is not in steady state but is in thermalDThe unit neither in steady state nor in thermal equilibrium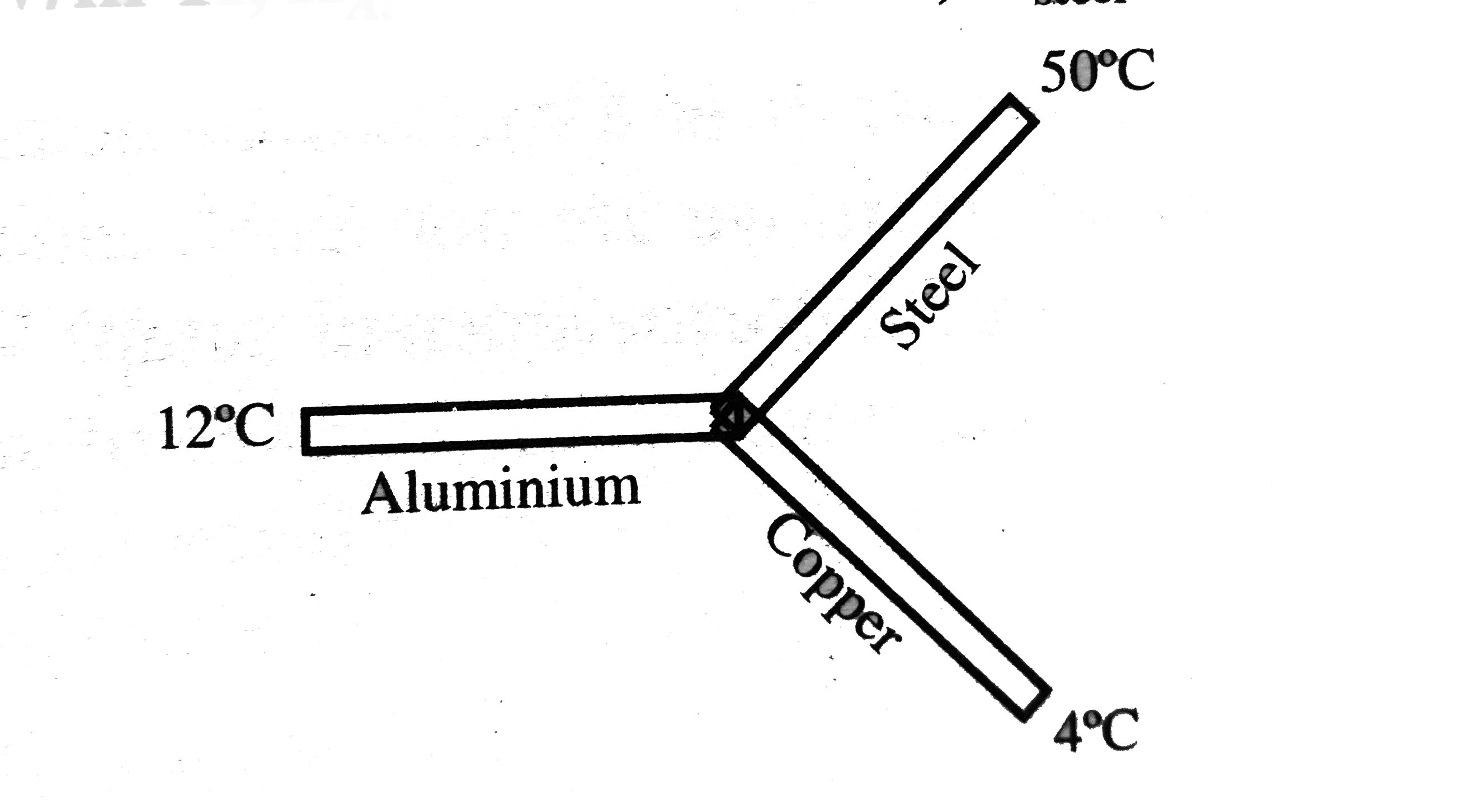
Three identical rods of length 1 m each, having cross-sectional area of 1cm2 each and made of aluminium, copper and steel, respectively, are maintained at temperatures of 12∘C,4∘C and 50∘C, respectively, at their separate ends. Find the temperature of their common junction.
[KCu=400W/m−K,KAl=200W/m−K,Ksteel=50W/m−K]A20∘CB10∘CC5∘CD8∘C
Find the thermal resistance of an aluminium rod of length 0.20 m and area of cross section 1×10−4m2. The heat current is along the length of the rod. [Thermal conductivity of aluminium=200Wm−1K−1]
View SolutionA steel rod of length 50 cm has a cross–sectional area of 0.4cm2. What force would be required to stretch this rod by the same amount as the expansion produced by heating it through 10∘C .
(α=10−5k−1 and Y=2×1011N/m2)
View SolutionFind the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionA thin metal disc of mass 0.5 kg and cross sectional area 0.05m2 is placed coaxially with a cylindrical block of height 0.5 m and same cross sectional area. The top face of the cylindrical block is maintained at a constant temperature of 300 K. If the initial temperature of the metal disc is 200 K, how long will it take for its temperature to raise to 250 K? The thermal conductivity of cylinder's material is 10Wm−1K−1 and specific heat capacity of disc's metal is 600Jkg−1K−1
Note: Consider that the thermal conductivity of disc is very high and the system is thermally insulated except the top face of cylinder.
View SolutionFigure-4.13 shows a water tank at a constant temperature. T0 and a small bodyof mass m, and specific heat S at a temperature T1 . Given that T1<T0. A metal rod of length L, cross-sectional area A whose thermal conductivity is K is placed between the tank and the body to connect than. Find the temperature of body as a function of time. Given that the heat capacity of rod is negligible.

View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution
